Location-allocation models involve two principal elements: 1) multiple facility location; and 2) the allocation of the services or products provided by those facilities to places of demand. Such models are used in the design of logistic systems like supply chains, especially warehouse and factory location, as well as in the location of public services. Public service location models involve objectives that often maximize access and levels of service, while private sector applications usually attempt to minimize cost. Such models are often hard to solve and involve the use of integer-linear programming software or sophisticated heuristics. Some models can be solved with functionality provided in GIS packages and other models are applied, loosely coupled, with GIS. We provide a short description of formulating two different models as well as discuss how they are solved.
Author and Citation Info:
Church, R. and Medrano, F.A. (2018). Location-allocation Modeling and GIS. The Geographic Information Science & Technology Body of Knowledge (3rd Quarter 2018 Edition), John P. Wilson (Ed). DOI: 10.22224/gistbok/2018.3.4.
This entry was published on September 15, 2018.
This Topic is also available in the following editions: DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Location-allocation modeling and p-median problems. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers.(2nd Quarter 2016, first digital).
Linear programming (LP) problem: a model consisting of continuous variables (often constrained to be non-negative in sign) and linear terms. It is comprised of an objective function whose value is to be optimized and a set of equality and inequality constraints. Such models can be very large, involving more than a million constraints and variables. Such problems can be solved in polynomial time (as a function of problem parameters).
NP (non-deterministic polynomial), a class of problems that is not considered to be solvable in polynomial time as a function of problem parameters. It is more likely that worst case instances of such problems are only solvable in exponential time.
Integer-linear programming (ILP) problem: an LP with additional integer-value restrictions on some or all of the variables. Such models are considerably more difficult to solve than LPs and, in most cases, involve computational complexities that are classified as NP.
NP-hard, a class of problems in NP that are considered to be at least as hard as the hardest to solve problems in the class NP. The traveling salesman problem is a member of this class of problems.
Heuristic, an approach that is designed to provide a feasible solution to a problem with no guarantee as to whether the solution is optimal or even close to optimal. Heuristics are usually developed to solve problems that are unusually hard to solve or to solve problems in a faster and more efficient manner, while sacrificing the prospect of guaranteeing an optimal result.
Location Science is rooted in the literature of location analysis that started with the works of von Thunen (1826) in terms of land-use allocation and Launhardt (1872) and Weber (1909) in terms of industrial location. The initial focus on industrial location was that of locating a production facility that needed raw materials, like iron ore, from localized deposits, and transporting the products to a market. Thus, arose the concept of a location triangle, like that depicted in Figure 1. This initial view of production and industrial location was devoid of an allocation component. As Launhardt and Weber concluded: to supply the market with a known demand of product, the production facility would need to transport raw materials from known sources of raw material to the industrial plant, manufacture the product, and then ship that product to the market. What was left in this puzzle was to locate the industrial plant so that costs of shipping the raw materials and finished product were minimized. Launhardt and Weber differed in their analysis by the fact that Launhardt considered the costs of building the transportation links (e.g. rail) between the factory and the raw material sources and the factory and the market as well as the costs of material and product shipments, whereas Weber assumed that transportation costs were some function of the Euclidean distance and only considered the shipment costs of the raw materials and product. This problem is a true location problem in the sense that one knows the interactions (or in this case the flows of materials and product) when siting the factory. Weber acknowledged that the location triangle represents a simple case of a more complicated problem of many markets and raw materials. However, despite the fact that there were potentially more markets and specific materials, flows or interactions between the factory and its needed materials as well as the factory and multiple markets were still fixed in quantity.
Figure 1. Location Triangle of Weber
Location-allocation problems differ from pure location problems in that flows of products and raw materials or the assignments of services are not known or fixed in advance and need to be determined as a part of the problem of location. Such cases arise when more than one facility is being located. Within the Weber paradigm, when multiple facilities are being located, then the value or cost of the service or transport is based upon which facility serves which market, that is, both facility placement and the allocation of markets to specific facilities must be determined in an optimal way.
There are a number of different types of location-allocation problems that have been developed in the last 50 years (Church and Murray, 2009). It is not possible to cover the wide range of location-allocation modeling in this introduction, but it is possible to cover two important and commonly used location-allocation models: the p-median problem (Hakimi, 1964, 1965) and the classic warehouse location problem (Geoffrion and McBride, 1978; Beasley 1988). Numerous location problems that are solved by companies and public sector agencies are related to one of these two problems. We begin in the next section with a description of the p-median problem.
One of the classic location-allocation problems is the p-median problem, which was originally defined by Hakimi (1964, 1965). This particular problem has the distinction of being one of the first to be incorporated into commercial GIS software. This problem is defined on a network of nodes and arcs, where nodes are defined as places of demand. This problem entails the location of p-facilities while minimizing the total weighted distance of servicing all demands. It is assumed that each demand will assign and be served by its closest located facility. Each node has an associated weight that represents the amount of demand at that node. The weighted distance in serving a given demand node is the weight of that node multiplied by the distance of the shortest path from that node to its closest facility. The implicit assumption in this problem is that each facility has the capacity to handle whatever amounts of demand that are assigned to it. Figure 2 depicts a 6 facility p-median solution for Santa Barbara County. This solution was generated by the Locate-Allocate heuristic provided in Network Analyst of ArcGIS Pro. This figure depicts a solution using a subset of census blocks for demands. Distances are measured using drive times on the road network. Each point has been given a demand that is weighted by the population of the block. This spider plot shows which demands are to be served by each facility.
Figure 2. A 6-median solution for Santa Barbara County depicted as a spider plot.
It has been shown that minimizing total weighted distance is equivalent to minimizing the average distance of service. Minimizing the average distance of service is a form of maximizing access. This is the main reason why the p-median problem is so popular in public facility location. Solving the p-median problem to optimality is computationally challenging and has been shown to be NP-hard.
Originally, Hakimi (1964) assumed that facilities could be placed anywhere on a network, at nodes or along arcs. Notable is the fact the he demonstrated that even though places on the arcs were allowed, there would always be one node of the network that was an optimal placement and was associated with the smallest total weighted distance of service in siting one facility. Hakimi (1965) extended this concept for multiple facilities, proving that at least one configuration of p-nodes will always be optimal for the p-facility problem. This property is known as a finite optimal set. Because of this property, virtually all p-median research since then has been based upon the assumption that facility sites will be restricted to nodes of the network.
The first step in solving a location-allocation problem to optimality is to formulate the problem as a mathematical programming problem. The first integer-linear programming formulation for the p-median problem was developed by ReVelle and Swain (1970). Consider the following notation:
j = an index used to refer to a specific facility site or node of a set of sites J
dij = the shortest distance between demand i and facility site j
ai = the weight associated with the demand at i
and decision variables (one representing location decisions and the other allocation decisions):
With this notation we can define the following p-median model:
(1) pMed: Minimize
Subject to:
(2)
(3)
(4)
(5)
(6)
The objective involves minimizing the total weighted distance in serving all demands by their closest located facility. The location component of the model is represented by the yi variables and the allocation component of the model is represented by the assignment variables, xij. When a given demand i assigns to a given facility site j, then the assignment/allocation variable, xij, will equal 1 in value. Constraints (2) force each demand to assign once, to some facility. Constraints (4) ensure that a demand i does not assign to a site j unless that site has been selected for a facility (i.e. yj= 1), for if a site j has not been selected for a facility then its corresponding yj value will equal zero and the constraint will prevent any demand assigning to it. Constraint (3) specifies that exactly p-sites will be selected for facility placement. Finally, constraints (5) and (6) specify the restrictions on the variables. There are two important properties to note here. The first is that each demand will assign to their closest located facility. Since the objective involves minimizing the weighted distance of assignment, the assignment that will minimize weighted distance will always be to the closest facility. Thus, the objective in concert with constraints (4) will ensure that assignments of a given demand will be made to the closest located facility. The second property is that there are no integer restrictions on the assignment variables, xij, even though it was defined as a binary integer variable. We know from the first property that a demand will assign to its closest facility. If there was a demand that assigned to two facilities (say .5 to one facility and .5 to the other), then these facilities must be equidistant from that demand, and a full assignment can be made to any one of the two facilities without changing the value of the objective. Consequently, it is not necessary to enforce binary values of the assignment variables.
The above model is an integer-linear programming (ILP) problem that can be solved using general purpose software, including commercial products such as IBM-Cplex, Gurobi, and FICO Xpress and free packages such as GLPK and COIN-OR. There are computational limits as to the size of a p-median problem that can be solved optimally; however, ongoing research has extended what can be solved optimally by new model formulations (e.g. Garcia et al. (2011) and Church (2008)) as well as specialized codes using an approach called Lagrangian Relaxation (Daskin and Maass, 2015). It is common to export data from a GIS, set up a model, like pMed, using a modeling language (e.g. Mosel or AMPL), solve the model using one of the commercial solvers, and then parse the solution and add it as a data layer in a GIS (a loosely coupled approach) so that the solution can be mapped.
There has been considerable research in developing quality heuristics for solving the p-median. This is typical in the field of Location Science (i.e. searching for good optimal approaches as well as heuristics), where problem size often dictates the need for a competitive heuristics. Teitz and Bart (1968) were the first to suggest a relatively robust heuristic solution approach for the p-median problem. Their process is quite simple, but also very effective. The basic steps are as follows:
Let be the set of all possible facility sites. Select at random p of the sites in for an initial solution. Let the set F be this new solution comprised of the p-sites. Remove these sites from the set . Go to step 2.
If is empty, go to step 3, otherwise select a candidate site and remove it from .
Evaluate the impact on total weighted distance if site k replaces any one of the p sites in F.
If any one of the possible swaps of candidate k for an existing site results in a reduction in total weighted distance, go to step c, otherwise go to step 2.
Swap candidate k with the site that results in the greatest improvement (reduction) in total weighted distance. Go to step 2.
A complete cycle of testing all possible candidates in swapping for exiting sites in F has been completed. If in that cycle any swaps were made, reset to be equal to all candidate sites except those in the current solution F and go to step 2, otherwise report the current solution F as the best solution found and stop.
Any given solution generated by the Teitz and Bart Heuristic is often quite good if not optimal. Most applications restart the Teitz and Bart heuristic 100’s or 1000’s of times to ensure that the best solution found is either optimal or very close to optimal. The final solution generated executing the Teitz and Bart heuristic is considered to be 1-opt. That is there are no 1-for-1 swaps of a facility site with an unused site that will result in an improvement in weighted distance. A 2-opt approach would find a solution which can’t be improved with any two facility sites being swapped with any two candidate sites. Thus, 2-opt is better than 1-opt, 3-opt is better than 2-opt, etc. and p-opt will result in finding a guaranteed optimal solution. Unfortunately, a p-opt search is combinatoric in nature and will result in exceedingly long computation times (years if not decades) for even small problems. Consequently, the Teitz and Bart heuristic is only used in a 1-opt mode.
Since the 1970s a number of heuristic search strategies have been developed, and many of these have been applied to solving the p-median problem. These include simulated annealing, genetic algorithms, variable neighborhood search, GRASP (Greedy Randomized Adaptive Search Procedure), and Tabu search, to name a few (see Mladenović, et al. 2007 for a review). A good example of this development is the use of GRASP with path-relinking that is deployed by Esri in the Location-Allocation function that can be found in the Network Analyst toolbox. The details of GRASP with path-relinking can be found in Resende and Werneck (2002) and involve using the GRASP approach to generate starting solutions, Teitz and Bart to generate improved solutions, and the path-relinking meta-heuristic to search for solutions that combine features of different solutions found by the Teitz and Bart process and stored in what is called an “Elite Pool.”
The p-median model is a rather malleable platform for solving location-allocation problems. For example, Church (1976) demonstrated that the maximal covering location problem could be solved as a p-median problem. The maximal covering problem involves the placement of p-facilities in such a way that as many of the demands are covered (served) within a maximal coverage standard (either a distance or time) of S (Church and ReVelle, 1974). To do this requires a specially defined distance matrix. Consider:
The above formulation of the p-median problem can be solved using the modified values instead of the actual distance values. This modified objective minimizes the total demand that is served beyond the distance of S, which is equivalent to maximizing the demand that is covered within S. Thus, a given maximal covering problem is convertible to an equivalent p-median problem. Hillsman (1984) demonstrated that other models could be formulated as equivalent p-median problems with “distance editing.” This is the approach taken in Esri software, where “distance editing” is used so that the location-allocation function that solves the p-median problem can also solve other related problems including the maximal covering location problem and the location set covering problem. Even though p-median equivalence via distance editing appears to be widespread in use, few if any tests have been performed to analyze whether this is a good approach for solving such problems when using heuristics (Murray, et al. 2018).
The classical warehouse location-allocation problem, simply called the warehouse location problem, involves locating a set of warehouses such that the transportation costs and facility costs in serving customers are minimized. The two main features where the warehouse location model differs from the p-median problem are: 1) warehouses can be capacitated and the allocation component is equivalent to the classical transportation problem (see The Classic Transportation Problem); and 2) the number of warehouses is not fixed in advanced but is endogenously determined. We can formulate this problem as an integer-linear programming problem, but first we should describe a switch of notation. Virtually all of the p-median literature formulates problems where index i is used to represent demands and index j is used to represent facilities, a historic use of notation that has persisted to this day. The warehouse location literature (which is sizable as well) has traditionally used notation that reverses the use of indices i and j. We follow that tradition here in formulating the warehouse location-allocation problem, so as to conform to the literature (Geoffrion and McBride, 1978). Consider the following notation:
i = an index used to refer to a specific warehouse location, in a set of sites I
j = an index used to refer to a specific customer location, in a set of customers J
ai = the potential capacity of warehouse site i, in units of product per time period
bj = the demand of customer j, in units of product per time period
cij = the per-unit cost of storing and transporting one unit of product from warehouse i to customer j
fi = the amortized fixed costs of establishing a warehouse at site i, per time period
(7) WHLP:
Subject to:
(8)
(9)
(10)
The objective involves minimizing the costs of transportation and costs of warehouse development. The constraints allocate product from the set of located warehouses among the demands so that all demands are met (constraint 8) and all warehouses work within their stated capacities (constraint 9). Note: conditions (10) are not necessary but are helpful in reducing the computation times when solving this problem with commercial ILP software. There are several other ways in which to formulate this problem, however the above formulation requires less computational effort than other forms in resolving fractional values of integer restricted variables in a branch-and-bound process used in ILP software. While the p-median model can be heuristically solved directly in GIS software like Esri’s Location-Allocation functionality, the WHLP is quite often solved outside of a GIS using commercial ILP software. Appropriate data is often exported from a GIS or other databases and incorporated into a model using a modeling language such as AMPL, Mosel, or APIs for common programming languages. After a problem instance is built, it is then solved using ILP software, and the resulting solution may then be imported back into a GIS for the purposes of mapping.
The two location-allocation problems presented here are representative of a large and diverse set of location problems that have been developed in the last 50 years. It would be impossible to review all of the related literature here, however, a greater understanding of the developments of this field can be found in Location Science (Laporte, et al. 2015).
In the past twenty years, little has changed with respect to how a location-allocation problem can be set up and solved using GIS functionality, like Esri’s locate-allocate command that can be found in the Network Analyst Toolbox. Such functionality is not unique and other systems like TransCAD are capable of solving such problems as well. But, the number of different models that can be solved is limited and there is an almost complete reliance on heuristics, when in some cases heuristics can be simply outclassed by state-of-the-art commercial optimization packages (Murray, et al. 2018). The demand for Location Analytics and more specific Business Analytics has spawned a whole new set of modeling and decision support tools. These include, for example, Microsoft’s Power BI, Carto, and Alteryx. Setting up and solving a location-allocation problem using many GIS packages requires a significant amount of user expertise. Companies such as Carto describe their products as a way to “escape the GIS handcuffs” with the capability of being able to “free yourself from reliance on legacy GIS products.”
As these products evolve, many analysts will no longer rely on using GIS to provide the location-allocation and location analytics capabilities, nor will they rely on GIS technicians to assist them in their analysis. A good example of this is the software developed by Alteryx. Alteryx provides many modeling capabilities for spatial and non-spatial problems. For spatial problems, one can process spatial data, produce a map, and solve relatively sophisticated location-allocation problems, using preprogrammed functions. There is also the capability to set up a model and use a commercial solver. This software provides drag and drop functionality where an analyst can drag and drop functions onto a modeling frame, connect such functions together, and specify options within each function to create visually a workflow that reads data, analyzes that data, solves a problem and produces a map. New functions and capabilities can be programmed in R or in other languages (e.g. Python) and integrated using COM model features. Without a doubt many analysts and companies will turn to such location-allocation modeling and mapping capabilities and rely less on traditional GIS systems. Unfortunately, this is not a panacea as there is often a lack of understanding the impacts of the Modifiable Area Unit Problem, the general propagation of error, the lack of capabilities to perform sensitivity analysis and search for robust solutions. There is an important role in which traditional GIS systems can play in this emerging market, but many new companies are emerging to capture that market of spatial analytics, including location-allocation modeling, without needing a costly legacy GIS system.
References:
Beasley, J. E. (1988). An algorithm for solving large capacitated warehouse location problems. European Journal of Operational Research, 33(3), 314-325.DOI: 10.1016/0377-2217(88)90175-0
Church, R. L. (2008). BEAMR: An exact and approximate model for the p-median problem. Computers & Operations Research, 35(2), 417-426. DOI: 10.1016/j.cor.2006.03.006
Church, R. L., & Murray, A. T. (2009). Business site selection, location analysis, and GIS. Hoboken, NJ: John Wiley & Sons.
Church, R., & ReVelle, C. (1974). The maximal covering location problem. Papers of the Regional Science Association 32(1), 101-118).
Church, R. L., & ReVelle, C. S. (1976). Theoretical and computational links between the p‐median, location set‐covering, and the maximal covering location problem. Geographical Analysis, 8(4), 406-415.
Daskin, M. S., & Maass, K. L. (2015). The p-median problem. In Location science (pp. 21-45). Springer International Publishing.
García, S., Labbé, M., & Marín, A. (2011). Solving large p-median problems with a radius formulation. INFORMS Journal on Computing, 23(4), 546-556. DOI: 10.1287/ijoc.1100.0418
Geoffrion, A., & McBride, R. M. (1978). Lagrangean relaxation applied to capacitated facility location problems. AIIE transactions, 10(1), 40-47.
Hakimi, S. L. (1964). Optimum locations of switching centers and the absolute centers and medians of a graph. Operations research, 12(3), 450-459.
Hakimi, S. L. (1965). Optimum distribution of switching centers in a communication network and some related graph theoretic problems. Operations research, 13(3), 462-475.
Hillsman, E. L. (1984). The p-median structure as a unified linear model for location—allocation analysis. Environment and Planning A, 16(3), 305-318.
Laporte, G., Nickel, S., & Saldanha da Gama, F. eds. (2015). Location Science (Vol. 528). Berlin: Springer
Launhardt, W. (1872). Kommercielle Tracirung der Verkehrswege. Architekten-und Ingenieurverein.
Mladenović, N., Brimberg, J., Hansen, P., & Moreno-Pérez, J. A. (2007). The p-median problem: A survey of metaheuristic approaches. European Journal of Operational Research, 179(3), 927-939. DOI: 10.1016/j.ejor.2005.05.034
Murray, A., Xu, J., Wang, Z. & Church, R.L. (2018). Commercial GIS Location Analytics: Capabilities and Performance. in review International Journal of Geographical Information Science.
Resende, M. G., & Werneck, R. F. (2002). A GRASP with path-relinking for the p-median problem. Journal of Heuristics.
ReVelle, C. S., & Swain, R. W. (1970). Central facilities location. Geographical analysis, 2(1), 30-42.
Teitz, M. B., & Bart, P. (1968). Heuristic methods for estimating the generalized vertex median of a weighted graph. Operations research, 16(5), 955-961.
von Thünen, J. H. (1826). Der isolierte Staat. Beziehung auf Landwirtschaft und Nationalökonomie.
Weber, A. (1909) Theory of the location of industries, translated by C.J. Friedrich (1929). University of Chicago Press.
Learning Objectives:
Describe the difference between a location-allocation and a pure location problem.
Describe why the following condition will hold when solving the WLP:
Describe the two basic approaches used to solve location-allocation models.
Describe why “distance editing” can be used to solve location problems related to the p-median problem.
Define NP-hard.
Instructional Assessment Questions:
1. Describe why a 1-median problem is a location problem and a p-median problem where is a location-allocation problem
2. Describe a public service in which you think the p-median is the ideal model for siting services.
3. If Esri’s ArcGIS is available with Network Analyst, use the Location-Allocation function to solve a p-median problem using a selected set of network nodes for demands and facility sites. Try selecting several different location models (e.g. maximal covering) and observe their differences using a spider plot.
4. If using a different GIS product, such as MapInfo Pro by Pitney Bowes or open-source QGIS, identify if location-allocation functionality is available and describe what techniques the software uses to solve such problems.
5. Identify software products (either open-source or commercial) that are available that can be used to create an ILP model using a modeling language where the resulting model can be solved by one or more commercial ILP software packages.
Location-allocation models involve two principal elements: 1) multiple facility location; and 2) the allocation of the services or products provided by those facilities to places of demand. Such models are used in the design of logistic systems like supply chains, especially warehouse and factory location, as well as in the location of public services. Public service location models involve objectives that often maximize access and levels of service, while private sector applications usually attempt to minimize cost. Such models are often hard to solve and involve the use of integer-linear programming software or sophisticated heuristics. Some models can be solved with functionality provided in GIS packages and other models are applied, loosely coupled, with GIS. We provide a short description of formulating two different models as well as discuss how they are solved.
Church, R. and Medrano, F.A. (2018). Location-allocation Modeling and GIS. The Geographic Information Science & Technology Body of Knowledge (3rd Quarter 2018 Edition), John P. Wilson (Ed). DOI: 10.22224/gistbok/2018.3.4.
This entry was published on September 15, 2018.
This Topic is also available in the following editions: DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Location-allocation modeling and p-median problems. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital).
1. Definitions
Linear programming (LP) problem: a model consisting of continuous variables (often constrained to be non-negative in sign) and linear terms. It is comprised of an objective function whose value is to be optimized and a set of equality and inequality constraints. Such models can be very large, involving more than a million constraints and variables. Such problems can be solved in polynomial time (as a function of problem parameters).
NP (non-deterministic polynomial), a class of problems that is not considered to be solvable in polynomial time as a function of problem parameters. It is more likely that worst case instances of such problems are only solvable in exponential time.
Integer-linear programming (ILP) problem: an LP with additional integer-value restrictions on some or all of the variables. Such models are considerably more difficult to solve than LPs and, in most cases, involve computational complexities that are classified as NP.
NP-hard, a class of problems in NP that are considered to be at least as hard as the hardest to solve problems in the class NP. The traveling salesman problem is a member of this class of problems.
Heuristic, an approach that is designed to provide a feasible solution to a problem with no guarantee as to whether the solution is optimal or even close to optimal. Heuristics are usually developed to solve problems that are unusually hard to solve or to solve problems in a faster and more efficient manner, while sacrificing the prospect of guaranteeing an optimal result.
2. What is Location-Allocation Modeling?
Location Science is rooted in the literature of location analysis that started with the works of von Thunen (1826) in terms of land-use allocation and Launhardt (1872) and Weber (1909) in terms of industrial location. The initial focus on industrial location was that of locating a production facility that needed raw materials, like iron ore, from localized deposits, and transporting the products to a market. Thus, arose the concept of a location triangle, like that depicted in Figure 1. This initial view of production and industrial location was devoid of an allocation component. As Launhardt and Weber concluded: to supply the market with a known demand of product, the production facility would need to transport raw materials from known sources of raw material to the industrial plant, manufacture the product, and then ship that product to the market. What was left in this puzzle was to locate the industrial plant so that costs of shipping the raw materials and finished product were minimized. Launhardt and Weber differed in their analysis by the fact that Launhardt considered the costs of building the transportation links (e.g. rail) between the factory and the raw material sources and the factory and the market as well as the costs of material and product shipments, whereas Weber assumed that transportation costs were some function of the Euclidean distance and only considered the shipment costs of the raw materials and product. This problem is a true location problem in the sense that one knows the interactions (or in this case the flows of materials and product) when siting the factory. Weber acknowledged that the location triangle represents a simple case of a more complicated problem of many markets and raw materials. However, despite the fact that there were potentially more markets and specific materials, flows or interactions between the factory and its needed materials as well as the factory and multiple markets were still fixed in quantity.
Figure 1. Location Triangle of Weber
Location-allocation problems differ from pure location problems in that flows of products and raw materials or the assignments of services are not known or fixed in advance and need to be determined as a part of the problem of location. Such cases arise when more than one facility is being located. Within the Weber paradigm, when multiple facilities are being located, then the value or cost of the service or transport is based upon which facility serves which market, that is, both facility placement and the allocation of markets to specific facilities must be determined in an optimal way.
There are a number of different types of location-allocation problems that have been developed in the last 50 years (Church and Murray, 2009). It is not possible to cover the wide range of location-allocation modeling in this introduction, but it is possible to cover two important and commonly used location-allocation models: the p-median problem (Hakimi, 1964, 1965) and the classic warehouse location problem (Geoffrion and McBride, 1978; Beasley 1988). Numerous location problems that are solved by companies and public sector agencies are related to one of these two problems. We begin in the next section with a description of the p-median problem.
3. The p-median problem
One of the classic location-allocation problems is the p-median problem, which was originally defined by Hakimi (1964, 1965). This particular problem has the distinction of being one of the first to be incorporated into commercial GIS software. This problem is defined on a network of nodes and arcs, where nodes are defined as places of demand. This problem entails the location of p-facilities while minimizing the total weighted distance of servicing all demands. It is assumed that each demand will assign and be served by its closest located facility. Each node has an associated weight that represents the amount of demand at that node. The weighted distance in serving a given demand node is the weight of that node multiplied by the distance of the shortest path from that node to its closest facility. The implicit assumption in this problem is that each facility has the capacity to handle whatever amounts of demand that are assigned to it. Figure 2 depicts a 6 facility p-median solution for Santa Barbara County. This solution was generated by the Locate-Allocate heuristic provided in Network Analyst of ArcGIS Pro. This figure depicts a solution using a subset of census blocks for demands. Distances are measured using drive times on the road network. Each point has been given a demand that is weighted by the population of the block. This spider plot shows which demands are to be served by each facility.
Figure 2. A 6-median solution for Santa Barbara County depicted as a spider plot.
It has been shown that minimizing total weighted distance is equivalent to minimizing the average distance of service. Minimizing the average distance of service is a form of maximizing access. This is the main reason why the p-median problem is so popular in public facility location. Solving the p-median problem to optimality is computationally challenging and has been shown to be NP-hard.
4. Solving the p-median problem
Originally, Hakimi (1964) assumed that facilities could be placed anywhere on a network, at nodes or along arcs. Notable is the fact the he demonstrated that even though places on the arcs were allowed, there would always be one node of the network that was an optimal placement and was associated with the smallest total weighted distance of service in siting one facility. Hakimi (1965) extended this concept for multiple facilities, proving that at least one configuration of p-nodes will always be optimal for the p-facility problem. This property is known as a finite optimal set. Because of this property, virtually all p-median research since then has been based upon the assumption that facility sites will be restricted to nodes of the network.
The first step in solving a location-allocation problem to optimality is to formulate the problem as a mathematical programming problem. The first integer-linear programming formulation for the p-median problem was developed by ReVelle and Swain (1970). Consider the following notation:
j = an index used to refer to a specific facility site or node of a set of sites J
dij = the shortest distance between demand i and facility site j
ai = the weight associated with the demand at i
and decision variables (one representing location decisions and the other allocation decisions):
With this notation we can define the following p-median model:
(1) pMed: Minimize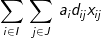
Subject to:
(2)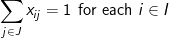
(3)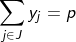
(4)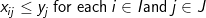
(5)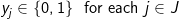
(6)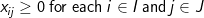
The objective involves minimizing the total weighted distance in serving all demands by their closest located facility. The location component of the model is represented by the yi variables and the allocation component of the model is represented by the assignment variables, xij. When a given demand i assigns to a given facility site j, then the assignment/allocation variable, xij, will equal 1 in value. Constraints (2) force each demand to assign once, to some facility. Constraints (4) ensure that a demand i does not assign to a site j unless that site has been selected for a facility (i.e. yj = 1), for if a site j has not been selected for a facility then its corresponding yj value will equal zero and the constraint will prevent any demand assigning to it. Constraint (3) specifies that exactly p-sites will be selected for facility placement. Finally, constraints (5) and (6) specify the restrictions on the variables. There are two important properties to note here. The first is that each demand will assign to their closest located facility. Since the objective involves minimizing the weighted distance of assignment, the assignment that will minimize weighted distance will always be to the closest facility. Thus, the objective in concert with constraints (4) will ensure that assignments of a given demand will be made to the closest located facility. The second property is that there are no integer restrictions on the assignment variables, xij, even though it was defined as a binary integer variable. We know from the first property that a demand will assign to its closest facility. If there was a demand that assigned to two facilities (say .5 to one facility and .5 to the other), then these facilities must be equidistant from that demand, and a full assignment can be made to any one of the two facilities without changing the value of the objective. Consequently, it is not necessary to enforce binary values of the assignment variables.
The above model is an integer-linear programming (ILP) problem that can be solved using general purpose software, including commercial products such as IBM-Cplex, Gurobi, and FICO Xpress and free packages such as GLPK and COIN-OR. There are computational limits as to the size of a p-median problem that can be solved optimally; however, ongoing research has extended what can be solved optimally by new model formulations (e.g. Garcia et al. (2011) and Church (2008)) as well as specialized codes using an approach called Lagrangian Relaxation (Daskin and Maass, 2015). It is common to export data from a GIS, set up a model, like pMed, using a modeling language (e.g. Mosel or AMPL), solve the model using one of the commercial solvers, and then parse the solution and add it as a data layer in a GIS (a loosely coupled approach) so that the solution can be mapped.
There has been considerable research in developing quality heuristics for solving the p-median. This is typical in the field of Location Science (i.e. searching for good optimal approaches as well as heuristics), where problem size often dictates the need for a competitive heuristics. Teitz and Bart (1968) were the first to suggest a relatively robust heuristic solution approach for the p-median problem. Their process is quite simple, but also very effective. The basic steps are as follows:
Any given solution generated by the Teitz and Bart Heuristic is often quite good if not optimal. Most applications restart the Teitz and Bart heuristic 100’s or 1000’s of times to ensure that the best solution found is either optimal or very close to optimal. The final solution generated executing the Teitz and Bart heuristic is considered to be 1-opt. That is there are no 1-for-1 swaps of a facility site with an unused site that will result in an improvement in weighted distance. A 2-opt approach would find a solution which can’t be improved with any two facility sites being swapped with any two candidate sites. Thus, 2-opt is better than 1-opt, 3-opt is better than 2-opt, etc. and p-opt will result in finding a guaranteed optimal solution. Unfortunately, a p-opt search is combinatoric in nature and will result in exceedingly long computation times (years if not decades) for even small problems. Consequently, the Teitz and Bart heuristic is only used in a 1-opt mode.
Since the 1970s a number of heuristic search strategies have been developed, and many of these have been applied to solving the p-median problem. These include simulated annealing, genetic algorithms, variable neighborhood search, GRASP (Greedy Randomized Adaptive Search Procedure), and Tabu search, to name a few (see Mladenović, et al. 2007 for a review). A good example of this development is the use of GRASP with path-relinking that is deployed by Esri in the Location-Allocation function that can be found in the Network Analyst toolbox. The details of GRASP with path-relinking can be found in Resende and Werneck (2002) and involve using the GRASP approach to generate starting solutions, Teitz and Bart to generate improved solutions, and the path-relinking meta-heuristic to search for solutions that combine features of different solutions found by the Teitz and Bart process and stored in what is called an “Elite Pool.”
5. Using the p-median model in solving other location problems
The p-median model is a rather malleable platform for solving location-allocation problems. For example, Church (1976) demonstrated that the maximal covering location problem could be solved as a p-median problem. The maximal covering problem involves the placement of p-facilities in such a way that as many of the demands are covered (served) within a maximal coverage standard (either a distance or time) of S (Church and ReVelle, 1974). To do this requires a specially defined distance matrix. Consider:
The above formulation of the p-median problem can be solved using the modified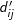 values instead of the actual distance values. This modified objective minimizes the total demand that is served beyond the distance of S, which is equivalent to maximizing the demand that is covered within S. Thus, a given maximal covering problem is convertible to an equivalent p-median problem. Hillsman (1984) demonstrated that other models could be formulated as equivalent p-median problems with “distance editing.” This is the approach taken in Esri software, where “distance editing” is used so that the location-allocation function that solves the p-median problem can also solve other related problems including the maximal covering location problem and the location set covering problem. Even though p-median equivalence via distance editing appears to be widespread in use, few if any tests have been performed to analyze whether this is a good approach for solving such problems when using heuristics (Murray, et al. 2018).
values instead of the actual distance values. This modified objective minimizes the total demand that is served beyond the distance of S, which is equivalent to maximizing the demand that is covered within S. Thus, a given maximal covering problem is convertible to an equivalent p-median problem. Hillsman (1984) demonstrated that other models could be formulated as equivalent p-median problems with “distance editing.” This is the approach taken in Esri software, where “distance editing” is used so that the location-allocation function that solves the p-median problem can also solve other related problems including the maximal covering location problem and the location set covering problem. Even though p-median equivalence via distance editing appears to be widespread in use, few if any tests have been performed to analyze whether this is a good approach for solving such problems when using heuristics (Murray, et al. 2018).
6. The Classic Warehouse Location Problem
The classical warehouse location-allocation problem, simply called the warehouse location problem, involves locating a set of warehouses such that the transportation costs and facility costs in serving customers are minimized. The two main features where the warehouse location model differs from the p-median problem are: 1) warehouses can be capacitated and the allocation component is equivalent to the classical transportation problem (see The Classic Transportation Problem); and 2) the number of warehouses is not fixed in advanced but is endogenously determined. We can formulate this problem as an integer-linear programming problem, but first we should describe a switch of notation. Virtually all of the p-median literature formulates problems where index i is used to represent demands and index j is used to represent facilities, a historic use of notation that has persisted to this day. The warehouse location literature (which is sizable as well) has traditionally used notation that reverses the use of indices i and j. We follow that tradition here in formulating the warehouse location-allocation problem, so as to conform to the literature (Geoffrion and McBride, 1978). Consider the following notation:
i = an index used to refer to a specific warehouse location, in a set of sites I
j = an index used to refer to a specific customer location, in a set of customers J
ai = the potential capacity of warehouse site i, in units of product per time period
bj = the demand of customer j, in units of product per time period
cij = the per-unit cost of storing and transporting one unit of product from warehouse i to customer j
fi = the amortized fixed costs of establishing a warehouse at site i, per time period
(7) WHLP:
Subject to:
(8)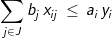
(9)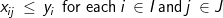
(10)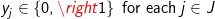
The objective involves minimizing the costs of transportation and costs of warehouse development. The constraints allocate product from the set of located warehouses among the demands so that all demands are met (constraint 8) and all warehouses work within their stated capacities (constraint 9). Note: conditions (10) are not necessary but are helpful in reducing the computation times when solving this problem with commercial ILP software. There are several other ways in which to formulate this problem, however the above formulation requires less computational effort than other forms in resolving fractional values of integer restricted variables in a branch-and-bound process used in ILP software. While the p-median model can be heuristically solved directly in GIS software like Esri’s Location-Allocation functionality, the WHLP is quite often solved outside of a GIS using commercial ILP software. Appropriate data is often exported from a GIS or other databases and incorporated into a model using a modeling language such as AMPL, Mosel, or APIs for common programming languages. After a problem instance is built, it is then solved using ILP software, and the resulting solution may then be imported back into a GIS for the purposes of mapping.
The two location-allocation problems presented here are representative of a large and diverse set of location problems that have been developed in the last 50 years. It would be impossible to review all of the related literature here, however, a greater understanding of the developments of this field can be found in Location Science (Laporte, et al. 2015).
7. Looking to the Future
In the past twenty years, little has changed with respect to how a location-allocation problem can be set up and solved using GIS functionality, like Esri’s locate-allocate command that can be found in the Network Analyst Toolbox. Such functionality is not unique and other systems like TransCAD are capable of solving such problems as well. But, the number of different models that can be solved is limited and there is an almost complete reliance on heuristics, when in some cases heuristics can be simply outclassed by state-of-the-art commercial optimization packages (Murray, et al. 2018). The demand for Location Analytics and more specific Business Analytics has spawned a whole new set of modeling and decision support tools. These include, for example, Microsoft’s Power BI, Carto, and Alteryx. Setting up and solving a location-allocation problem using many GIS packages requires a significant amount of user expertise. Companies such as Carto describe their products as a way to “escape the GIS handcuffs” with the capability of being able to “free yourself from reliance on legacy GIS products.”
As these products evolve, many analysts will no longer rely on using GIS to provide the location-allocation and location analytics capabilities, nor will they rely on GIS technicians to assist them in their analysis. A good example of this is the software developed by Alteryx. Alteryx provides many modeling capabilities for spatial and non-spatial problems. For spatial problems, one can process spatial data, produce a map, and solve relatively sophisticated location-allocation problems, using preprogrammed functions. There is also the capability to set up a model and use a commercial solver. This software provides drag and drop functionality where an analyst can drag and drop functions onto a modeling frame, connect such functions together, and specify options within each function to create visually a workflow that reads data, analyzes that data, solves a problem and produces a map. New functions and capabilities can be programmed in R or in other languages (e.g. Python) and integrated using COM model features. Without a doubt many analysts and companies will turn to such location-allocation modeling and mapping capabilities and rely less on traditional GIS systems. Unfortunately, this is not a panacea as there is often a lack of understanding the impacts of the Modifiable Area Unit Problem, the general propagation of error, the lack of capabilities to perform sensitivity analysis and search for robust solutions. There is an important role in which traditional GIS systems can play in this emerging market, but many new companies are emerging to capture that market of spatial analytics, including location-allocation modeling, without needing a costly legacy GIS system.
Beasley, J. E. (1988). An algorithm for solving large capacitated warehouse location problems. European Journal of Operational Research, 33(3), 314-325.DOI: 10.1016/0377-2217(88)90175-0
Church, R. L. (2008). BEAMR: An exact and approximate model for the p-median problem. Computers & Operations Research, 35(2), 417-426. DOI: 10.1016/j.cor.2006.03.006
Church, R. L., & Murray, A. T. (2009). Business site selection, location analysis, and GIS. Hoboken, NJ: John Wiley & Sons.
Church, R., & ReVelle, C. (1974). The maximal covering location problem. Papers of the Regional Science Association 32(1), 101-118).
Church, R. L., & ReVelle, C. S. (1976). Theoretical and computational links between the p‐median, location set‐covering, and the maximal covering location problem. Geographical Analysis, 8(4), 406-415.
Daskin, M. S., & Maass, K. L. (2015). The p-median problem. In Location science (pp. 21-45). Springer International Publishing.
García, S., Labbé, M., & Marín, A. (2011). Solving large p-median problems with a radius formulation. INFORMS Journal on Computing, 23(4), 546-556. DOI: 10.1287/ijoc.1100.0418
Geoffrion, A., & McBride, R. M. (1978). Lagrangean relaxation applied to capacitated facility location problems. AIIE transactions, 10(1), 40-47.
Hakimi, S. L. (1964). Optimum locations of switching centers and the absolute centers and medians of a graph. Operations research, 12(3), 450-459.
Hakimi, S. L. (1965). Optimum distribution of switching centers in a communication network and some related graph theoretic problems. Operations research, 13(3), 462-475.
Hillsman, E. L. (1984). The p-median structure as a unified linear model for location—allocation analysis. Environment and Planning A, 16(3), 305-318.
Laporte, G., Nickel, S., & Saldanha da Gama, F. eds. (2015). Location Science (Vol. 528). Berlin: Springer
Launhardt, W. (1872). Kommercielle Tracirung der Verkehrswege. Architekten-und Ingenieurverein.
Mladenović, N., Brimberg, J., Hansen, P., & Moreno-Pérez, J. A. (2007). The p-median problem: A survey of metaheuristic approaches. European Journal of Operational Research, 179(3), 927-939. DOI: 10.1016/j.ejor.2005.05.034
Murray, A., Xu, J., Wang, Z. & Church, R.L. (2018). Commercial GIS Location Analytics: Capabilities and Performance. in review International Journal of Geographical Information Science.
Resende, M. G., & Werneck, R. F. (2002). A GRASP with path-relinking for the p-median problem. Journal of Heuristics.
ReVelle, C. S., & Swain, R. W. (1970). Central facilities location. Geographical analysis, 2(1), 30-42.
Teitz, M. B., & Bart, P. (1968). Heuristic methods for estimating the generalized vertex median of a weighted graph. Operations research, 16(5), 955-961.
von Thünen, J. H. (1826). Der isolierte Staat. Beziehung auf Landwirtschaft und Nationalökonomie.
Weber, A. (1909) Theory of the location of industries, translated by C.J. Friedrich (1929). University of Chicago Press.
1. Describe why a 1-median problem is a location problem and a p-median problem where is a location-allocation problem
2. Describe a public service in which you think the p-median is the ideal model for siting services.
3. If Esri’s ArcGIS is available with Network Analyst, use the Location-Allocation function to solve a p-median problem using a selected set of network nodes for demands and facility sites. Try selecting several different location models (e.g. maximal covering) and observe their differences using a spider plot.
4. If using a different GIS product, such as MapInfo Pro by Pitney Bowes or open-source QGIS, identify if location-allocation functionality is available and describe what techniques the software uses to solve such problems.
5. Identify software products (either open-source or commercial) that are available that can be used to create an ILP model using a modeling language where the resulting model can be solved by one or more commercial ILP software packages.
Keywords: