Analytics and Modeling

This knowledge area embodies a variety of data driven analytics, geocomputational methods, simulation and model driven approaches designed to study complex spatial-temporal problems, develop insights into characteristics of geospatial data sets, create and test geospatial process models, and construct knowledge of the behavior of geographically-explicit and dynamic processes and their patterns.

Topics in this Knowledge Area are listed thematically below. Existing topics are in regular font and linked directly to their original entries (published in 2006; these contain only Learning Objectives). Entries that have been updated and expanded are in bold. Forthcoming, future topics are italicized. 

 

Methodological Context Surface & Field Analyses Space-Time Analysis & Modeling
Geospatial Analysis & Model Building Modeling Surfaces Time Geography
Changing Context of GIScience Gridding, Interpolation, and Contouring Capturing Spatio-Temporal Dynamics in Computational Modeling 
Building Blocks Inverse Distance Weighting GIS-Based Computational Modeling
Overlay & Combination Operations Radial Basis & Spline Functions Computational Movement Analysis
Areal Interpolation Polynomial Functions Volumes and Space-Time Volumes
Aggregation of Spatial Entities Kriging Interpolation  
Classification & Clustering LiDAR Point Cloud Analysis Geocomputational Methods & Models
Boundaries & Zone Membership Intervisibility, Line-of-Sight, and Viewsheds Cellular Automata
Spatial Queries Digital Elevation Models & Terrain Metrics Agent-based Modeling
Buffers TIN-based Models and Terrain Metrics Simulation Modeling
Grid Operations & Map Algebra Watersheds & Drainage Networks Artificial Neural Networks
Data Exploration & Spatial Statistics 3D Parametric Surfaces Genetic Algorithms & Evolutionary Computing 
Spatial Statistics Network & Location Analysis Big Data & Geospatial Analysis
Spatial Sampling for Spatial Analysis Intro to Network & Location Analysis Problems of Large Spatial Databases
Exploratory Spatial Data Analysis (ESDA) Location & Service Area Problems Pattern Recognition & Matching
Point Pattern Analysis Network Route & Tour Problems Artificial Intelligence Approaches
Kernels & Density Estimation Modelling Accessibility Intro to Spatial Data Mining
Spatial Interaction Location-allocation Modeling Rule Learning for Spatial Data Mining
Cartographic Modeling The Classic Transportation Problem Machine Learning Approaches
Multi-criteria Evaluation   CyberGIS and Cyberinfrastructure
Grid-based Statistics and Metrics   Analysis of Errors & Uncertainty
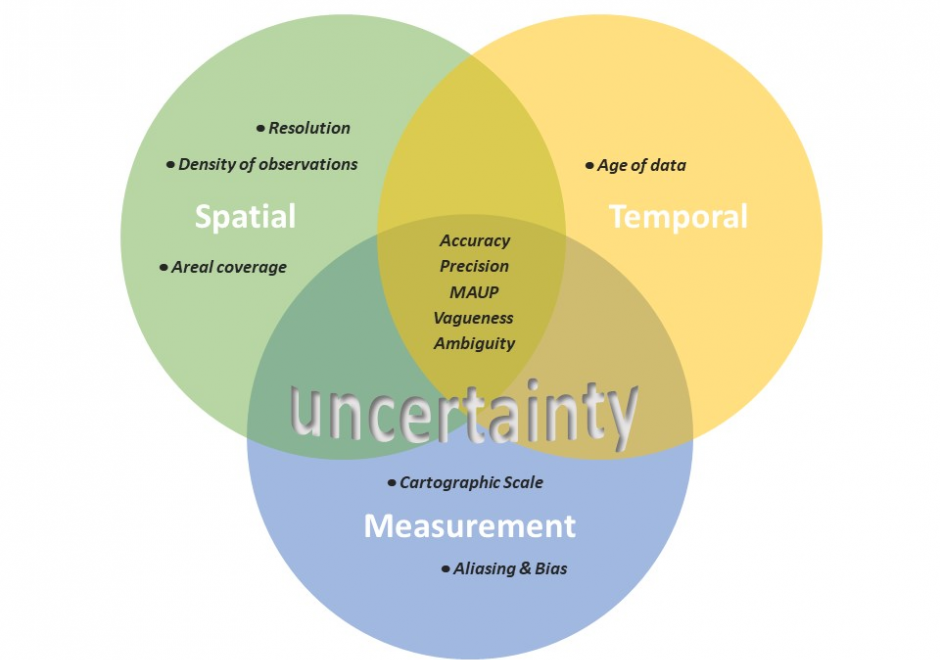
Landscape Metrics   Error-based Uncertainty
Hot-spot and Cluster Analysis   Conceptual Models of Error & Uncertainty
Global Measures of Spatial Association   Spatial Data Uncertainty
Local Indicators of Spatial Autocorrelation   Problems of Scale & Zoning
Simple Regression & Trend Surface Analysis   Thematic Accuracy & Assessment
Geographically Weighted Regression   Stochastic Simulation & Monte Carlo Methods
Spatial Autoregressive Models   Mathematical Models of Uncertainty
Spatial Filtering Models   Fuzzy Aggregation Operators

 

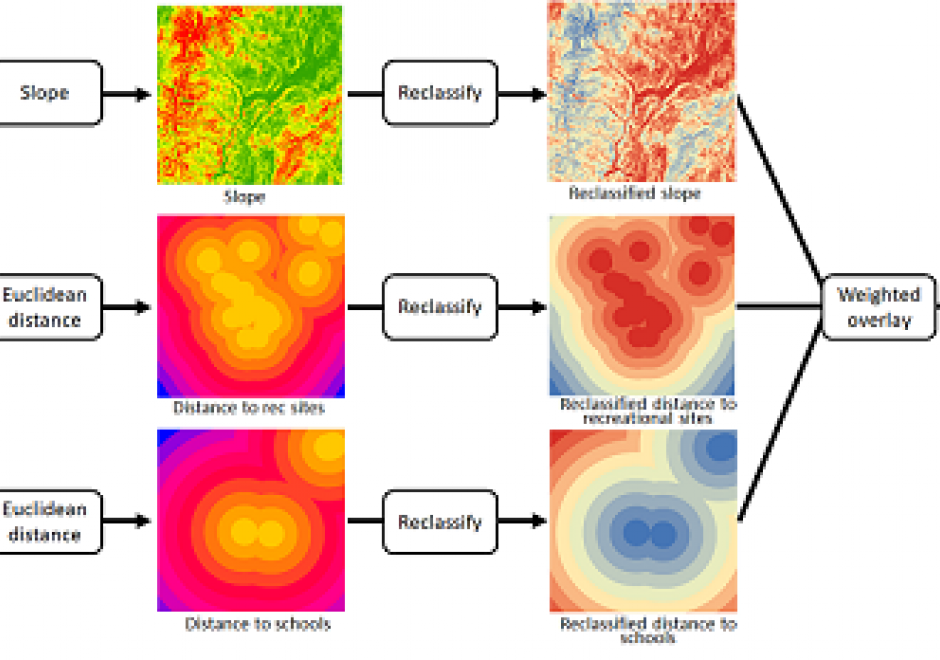
AM-90 - Computational Movement Analysis

Figure 1. Group movement patterns as illustrated in this coordinated escape behavior of a group of mountain goat (Rubicapra rubicapra) evading approaching hikers on the Fuorcla Trupchun near the Italian/Swiss border are at the core of computational movement analysis. Once the trajectories of moving objects are collected and made accessible for computational processing, CMA aims at a better understanding of the characteristics of movement processes of animals, people or things in geographic space.

 

Computational Movement Analysis (CMA) develops and applies analytical computational tools aiming at a better understanding of movement data. CMA copes with the rapidly growing data streams capturing the mobility of people, animals, and things roaming geographic spaces. CMA studies how movement can be represented, modeled, and analyzed in GIS&T. The CMA toolbox includes a wide variety of approaches, ranging from database research, over computational geometry to data mining and visual analytics.

AM-57 - Data conversion
  • Identify the conceptual and practical difficulties associated with data model and format conversion
  • Convert a data set from the native format of one GIS product to another
  • Discuss the role of metadata in facilitating conversation of data models and data structures between systems
  • Describe a workflow for converting and implementing a data model in a GIS involving an Entity-Relationship (E-R) diagram and the Universal Modeling Language (UML)
AM-106 - Error-based Uncertainty

The largest contributing factor to spatial data uncertainty is error. Error is defined as the departure of a measure from its true value. Uncertainty results from: (1) a lack of knowledge of the extent and of the expression of errors and  (2) their propagation through analyses. Understanding error and its sources is key to addressing error-based uncertainty in geospatial practice. This entry presents a sample of issues related to error and error based uncertainty in spatial data. These consist of (1) types of error in spatial data, (2) the special case of scale and its relationship to error and (3) approaches to quantifying error in spatial data.

AM-19 - Exploratory data analysis (EDA)
  • Describe the statistical characteristics of a set of spatial data using a variety of graphs and plots (including scatterplots, histograms, boxplots, q–q plots)
  • Select the appropriate statistical methods for the analysis of given spatial datasets by first exploring them using graphic methods
AM-41 - Flow modeling
  • Describe practical situations in which flow is conserved while splitting or joining at nodes of the network
  • Apply a maximum flow algorithm to calculate the largest flow from a source to a sink, using the edges of the network, subject to capacity constraints on the arcs and the conservation of flow
  • Explain how the concept of capacity represents an upper limit on the amount of flow through the network
  • Demonstrate how capacity is assigned to edges in a network using the appropriate data structure
AM-88 - Fuzzy aggregation operators
  • Compare and contrast Boolean and fuzzy logical operations
  • Compare and contrast several operators for fuzzy aggregation, including those for intersect and union
  • Exemplify one use of fuzzy aggregation operators
  • Describe how an approach to map overlay analysis might be different if region boundaries were fuzzy rather than crisp
  • Describe fuzzy aggregation operators
AM-78 - Genetic Algorithms and Evolutionary Computing

Genetic algorithms (GAs) are a family of search methods that have been shown to be effective in finding optimal or near-optimal solutions to a wide range of optimization problems. A GA maintains a population of solutions to the problem being solved and uses crossover, mutation, and selection operations to iteratively modify them. As the population evolves across generations, better solutions are created and inferior ones are selectively discarded. GAs usually run for a fixed number of iterations (generations) or until further improvements do not obtain. This contribution discusses the fundamental principles of genetic algorithms and uses Python code to illustrate how GAs can be developed for both numerical and spatial optimization problems. Computational experiments are used to demonstrate the effectiveness of GAs and to illustrate some nuances in GA design.

AM-20 - Geospatial Analysis and Model Building

Spatial modeling is an important instrument to conduct geospatial analysis to understand the world and guide decision-making. In GIS, spatial models are formal languages to express mechanisms of geographic processes and design analytical workflows to understand these processes. With the development of GIS and computer science, various types of spatial models and modeling techniques have become available, which endows the term of “spatial model” with different meanings. This entry provides an overview of common types of spatial models, modeling techniques, and related applications.

AM-81 - GIS-Based Computational Modeling

GIS-based computational models are explored. While models vary immensely across disciplines and specialties, the focus is on models that simulate and forecast geographical systems and processes in time and space. The degree and means of integration of the many different models with GIS are covered, and the critical phases of modeling: design, implementation, calibration, sensitivity analysis, validation and error analysis are introduced. The use of models in simulations, an important purpose for implementing models within or outside of GIS, is discussed and the context of scenario-based planning explained. To conclude, a survey of model types is presented, with their application methods and some examples, and the goals of modeling are discussed.

AM-22 - Global Measures of Spatial Association

Spatial association broadly describes how the locations and values of samples or observations vary across space. Similarity in both the attribute values and locations of observations can be assessed using measures of spatial association based upon the first law of geography. In this entry, we focus on the measures of spatial autocorrelation that assess the degree of similarity between attribute values of nearby observations across the entire study region. These global measures assess spatial relationships with the combination of spatial proximity as captured in the spatial weights matrix and the attribute similarity as captured by variable covariance (i.e. Moran’s I) or squared difference (i.e. Geary’s C). For categorical data, the join count statistic provides a global measure of spatial association. Two visualization approaches for spatial autocorrelation measures include Moran scatterplots and variograms (also known as semi-variograms).

Pages