AM-42 - The Classic Transportation Problem
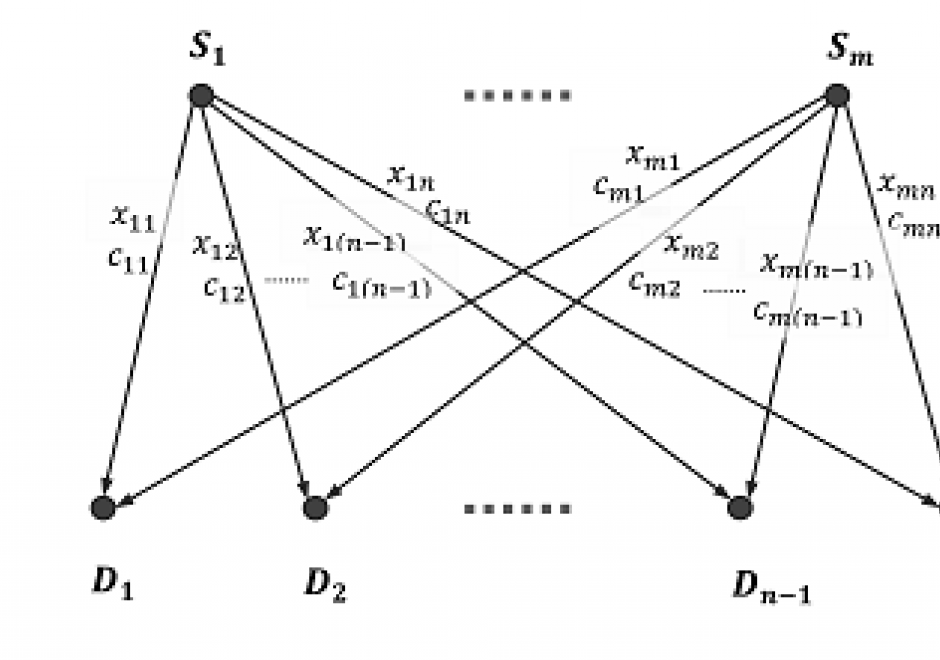
The classic transportation problem concerns minimizing the cost of transporting a product from sources/supplies to destinations/demands. It is a network-flow problem that arises in industrial logistics and is often solved by linear programming (LP). The three inputs of the model are total units produced at each source, total units needed at each destination, and the cost to transport one unit from each source to each destination. And the objective is to minimize the total cost of transporting all units produced at sources to meet the demands at destinations. The problem solution includes three basic steps: 1) finding an initial basic feasible solution, 2) checking if the current solution is optimal (with the lowest costs), and improving the current solution through iteration. Solving such a problem relies strongly on the network data models, least-cost path algorithms, other functionalities in GIS. And an integrated framework is often adopted to utilize both GIS and non-GIS linear programming solvers to search for the optimal solution.

FC-19 - Networks
A network is a widely used term with different definitions and methodologies depending on the applications. In GIS, a network refers to an arrangement of elements (i.e., nodes, links) and information on their connections and interactions. There are two types of networks: physical and logical. While a physical network has tangible objects (e.g., road segments), a logical network represents logical connections among nodes and links. A network can be represented with a mathematical notion called graph theory. Different network components are utilized to describe characteristics of a network including loops, walks, paths, circuits, and parallel edges. Network data are commonly organized in a vector format with network topology, specifically connectivity among nodes and links, whereas raster data can be also utilized for a least-cost problem over continuous space. Network data is utilized in a wide range of network analyses, including the classic shortest path problem.