AM-21 - The Evolution of Geospatial Reasoning, Analytics, and Modeling
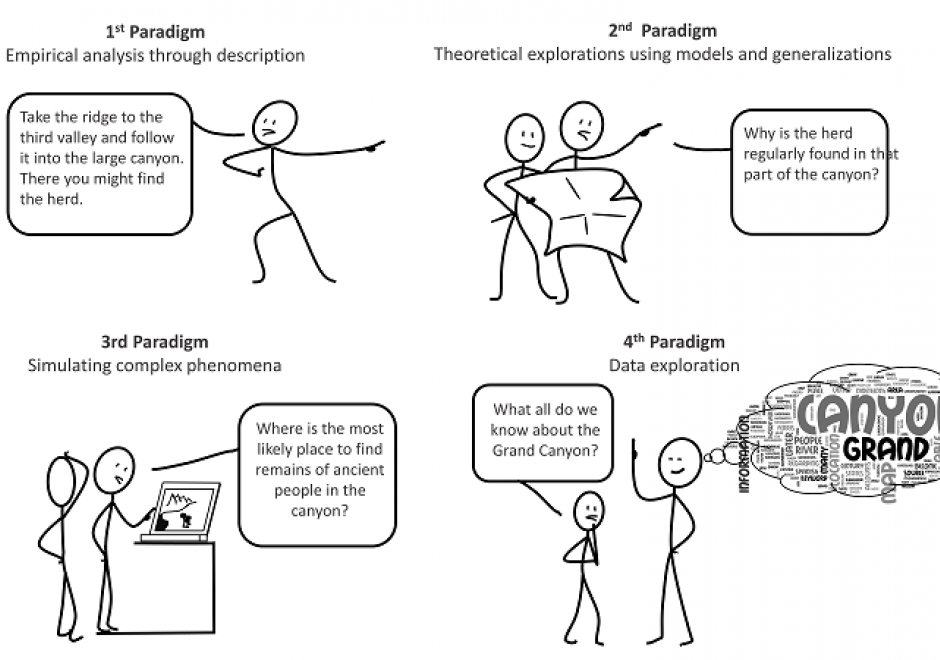
The field of geospatial analytics and modeling has a long history coinciding with the physical and cultural evolution of humans. This history is analyzed relative to the four scientific paradigms: (1) empirical analysis through description, (2) theoretical explorations using models and generalizations, (3) simulating complex phenomena and (4) data exploration. Correlations among developments in general science and those of the geospatial sciences are explored. Trends identify areas ripe for growth and improvement in the fourth and current paradigm that has been spawned by the big data explosion, such as exposing the ‘black box’ of GeoAI training and generating big geospatial training datasets. Future research should focus on integrating both theory- and data-driven knowledge discovery.


AM-42 - The Classic Transportation Problem
The classic transportation problem concerns minimizing the cost of transporting a product from sources/supplies to destinations/demands. It is a network-flow problem that arises in industrial logistics and is often solved by linear programming (LP). The three inputs of the model are total units produced at each source, total units needed at each destination, and the cost to transport one unit from each source to each destination. And the objective is to minimize the total cost of transporting all units produced at sources to meet the demands at destinations. The problem solution includes three basic steps: 1) finding an initial basic feasible solution, 2) checking if the current solution is optimal (with the lowest costs), and improving the current solution through iteration. Solving such a problem relies strongly on the network data models, least-cost path algorithms, other functionalities in GIS. And an integrated framework is often adopted to utilize both GIS and non-GIS linear programming solvers to search for the optimal solution.