KE-01 - The process of GIS&T design

- Describe the major approaches to the design of geospatial systems
- Analyze past cases to identify best practices of design and implementation
- Compare and contrast the relative merits of the use-case driven and architecture-centric design processes


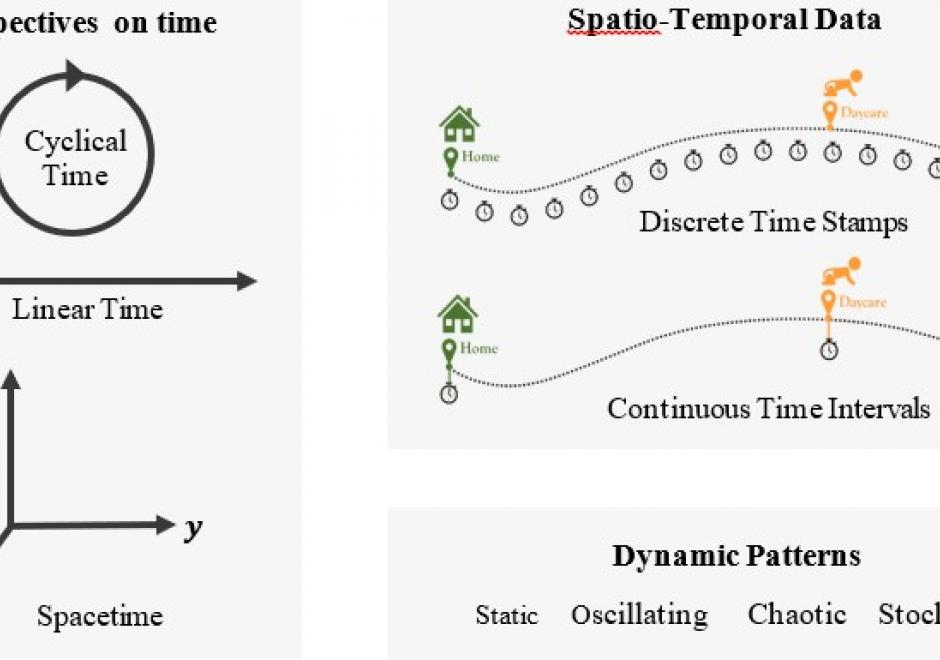
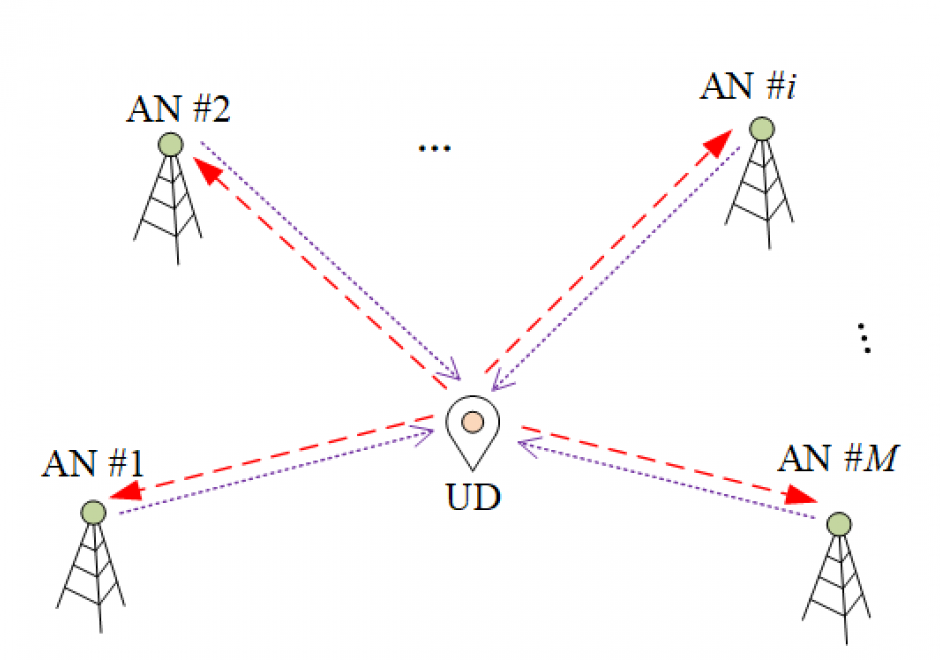

FC-20 - The power of maps