DM-23 - Fields in space and time

- Define a field in terms of properties, space, and time
- Formalize the notion of field using mathematical functions and calculus
- Recognize the influences of scale on the perception and meaning of fields
- Evaluate the field view’s description of “objects” as conceptual discretizations of continuous patterns
- Identify applications and phenomena that are not adequately modeled by the field view
- Identify examples of discrete and continuous change found in spatial, temporal, and spatio-temporal fields
- Relate the notion of field in GIS to the mathematical notions of scalar and vector fields
- Differentiate various sources of fields, such as substance properties (e.g., temperature), artificial constructs (e.g., population density), and fields of potential or influence (e.g., gravity)

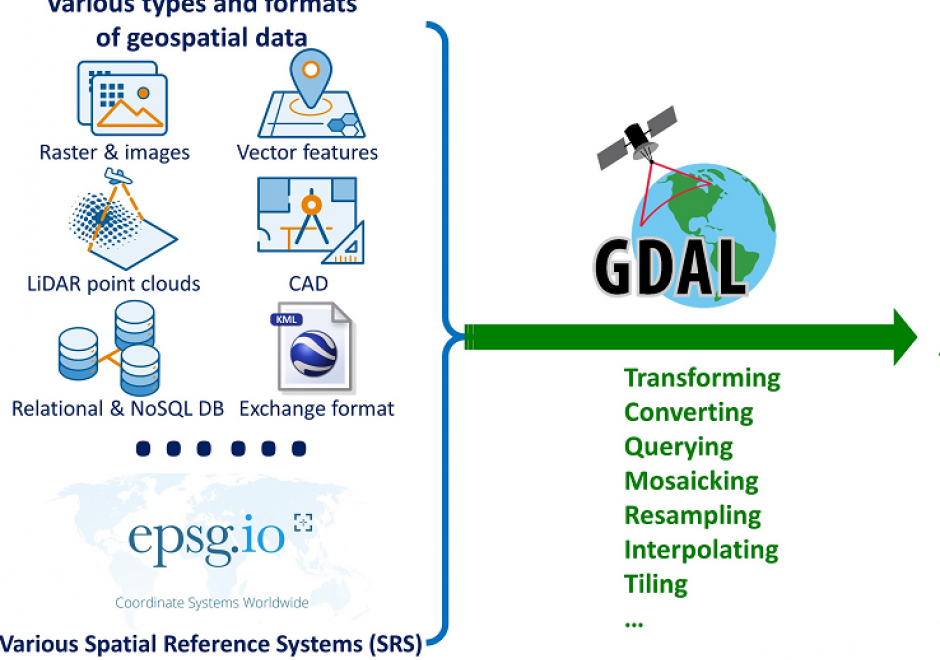
DC-09 - Field data technologies