GS-25 - Spatial Decision Support

It has been estimated that 80% of all datasets include geographic references. Since these data often factor into preparing important decisions, we can assume that a significant proportion of all decisions have a geospatial aspect to them. Therefore, spatial decision support is an intrinsic component of societal decision-making. It is thus necessary for current and aspiring analysts, and for decision-makers and other stakeholders, to understand the fundamental concepts, techniques, and challenges of spatial decision support. This GIS&T topic explores the unique nature and basic concepts of spatial decision support, discusses the relationship between Spatial Decision Support Systems (SDSS) and Geographic Information Systems (GIS), and briefly introduces Multi-Criteria Decision Analysis (MCDA) as a decision support technique. The impact of Web-based and mobile information technology, ever-increasing accessibility of geospatial data, and participatory approaches to decision-making are touched upon and additional resources for further reading provided.


AM-107 - Spatial Data Uncertainty
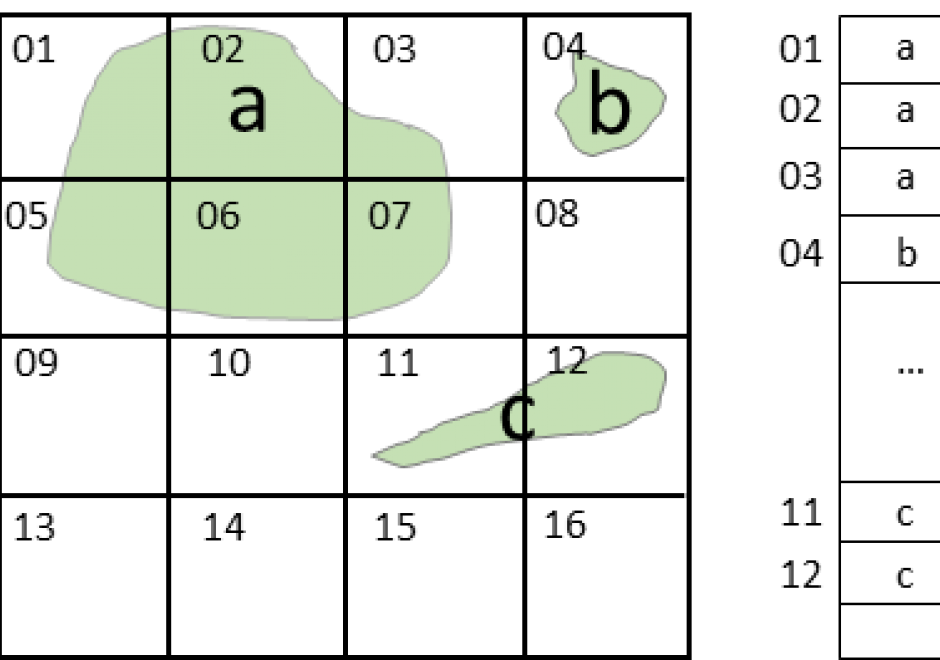
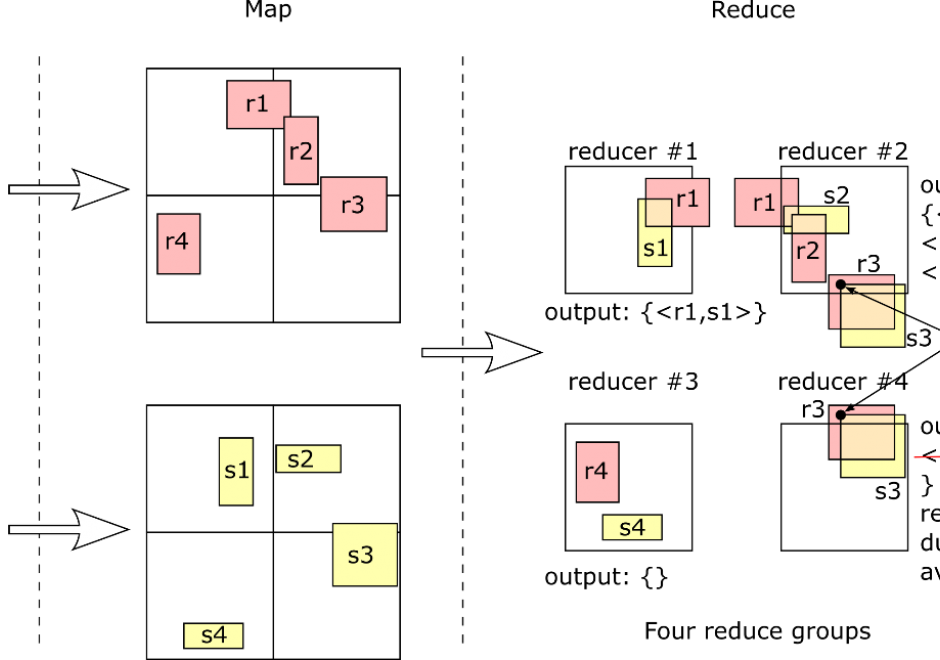
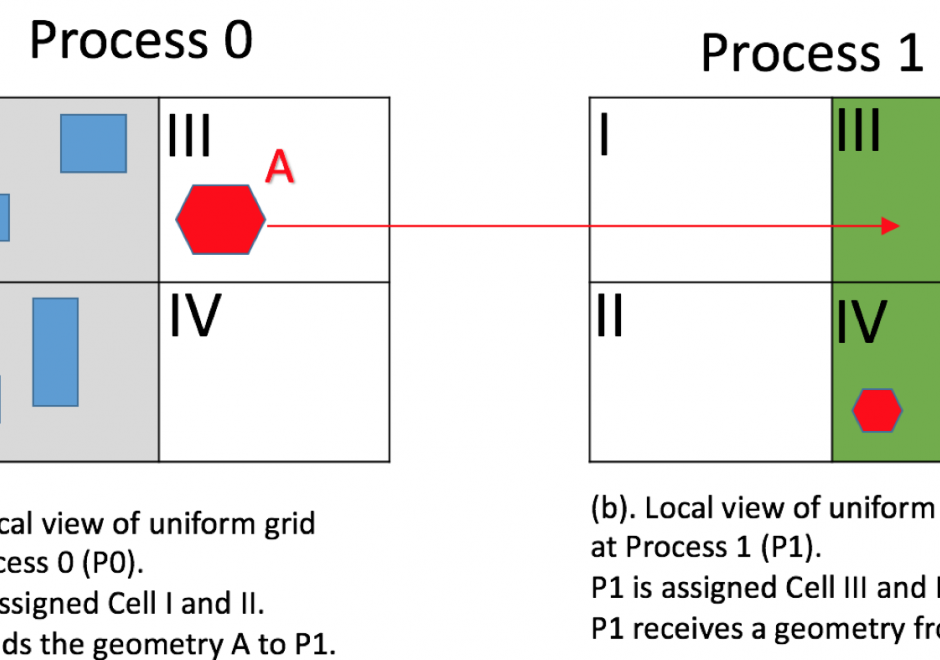
Although spatial data users may not be aware of the inherent uncertainty in all the datasets they use, it is critical to evaluate data quality in order to understand the validity and limitations of any conclusions based on spatial data. Spatial data uncertainty is inevitable as all representations of the real world are imperfect. This topic presents the importance of understanding spatial data uncertainty and discusses major methods and models to communicate, represent, and quantify positional and attribute uncertainty in spatial data, including both analytical and simulation approaches. Geo-semantic uncertainty that involves vague geographic concepts and classes is also addressed from the perspectives of fuzzy-set approaches and cognitive experiments. Potential methods that can be implemented to assess the quality of large volumes of crowd-sourced geographic data are also discussed. Finally, this topic ends with future directions to further research on spatial data quality and uncertainty.