You are currently viewing an archived version of Topic An Introduction to Spatial Data Mining.
If updates or revisions have been published you can find them at An Introduction to Spatial Data Mining.
The goal of spatial data mining is to discover potentially useful, interesting, and non-trivial patterns from spatial data-sets (e.g., GPS trajectory of smartphones). Spatial data mining is societally important having applications in public health, public safety, climate science, etc. For example, in epidemiology, spatial data mining helps to nd areas with a high concentration of disease incidents to manage disease outbreaks. Computational methods are needed to discover spatial patterns since the volume and velocity of spatial data exceed the ability of human experts to analyze it. Spatial data has unique characteristics like spatial autocorrelation and spatial heterogeneity which violate the i.i.d (Independent and Identically Distributed) assumption of traditional statistic and data mining methods. Therefore, using traditional methods may miss patterns or may yield spurious patterns, which are costly in societal applications. Further, there are additional challenges such as MAUP (Modiable Areal Unit Problem) as illustrated by a recent court case debating gerrymandering in elections. In this article, we discuss tools and computational methods of spatial data mining, focusing on the primary spatial pattern families: hotspot detection, collocation detection, spatial prediction, and spatial outlier detection. Hotspot detection methods use domain information to accurately model more active and high-density areas. Collocation detection methods find objects whose instances are in proximity to each other in a location. Spatial prediction approaches explicitly model the neighborhood relationship of locations to predict target variables from input features. Finally, spatial outlier detection methods find data that differ from their neighbors. Lastly, we describe future research and trends in spatial data mining.
Author and Citation Info:
Golmohammadi, J., Xie, Y., Gupta, J., Farhadloo, M., Li, Y., Cai, J., Detor, S., Roh, A., Shekhar, S. (2020). An Introduction to Spatial Data Mining. The Geographic Information Science & Technology Body of Knowledge (4th Quarter 2020 Edition), John P. Wilson (Ed.). DOI:10.22224/gistbok/2020.4.5..
This entry was first published on November 20, 2020. No earlier editions exist.
This article is supported by National Science Foundation under Grant No.1541876, 1029711, 1737633, IIS-1320580 , IIS-0940818, and IIS-1218168 , the USDOD under Grants No.HM1582-08-1-0017 and HM0210-13-1-0005, the Advanced Research Projects Agency-Energy (ARPA-E), U.S. Department of Energy under Award No.DE-AR0000795, the NIH under Grant No. UL1 TR002494, KL2TR002492, and TL1 TR002493, the USDA under Grant No.2017-51181-27222, and the OVPR Infrastructure Investment Initiative, Minnesota Supercomputing Institute (MSI), and Provost’s Grand Challenges Exploratory Research and International Enhancements Grants at the University of Minnesota. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. Also, we appreciate Kim Koffolt’s helpful comments and feedbacks for enhancing readability of the paper.
Spatial data: Any data that includes location information such as street address, or longitude and latitude.
Independent and Identically Distributed (i.i.d) assumption: A classical assumption in statistics that presumes data samples to be independent of each other and are distributed identically.
Spatial autocorrelation: It is defined as a measure of dependency among points in a spatial neighborhood. The dependency of spatial data rejects the independence assumption of classical statistics.
Spatial heterogeneity (or spatial non-stationarity): It refers to the variation in events, features and relationships across a region. It violates the assumption of identical distribution.
Spatial continuity: It refers to the presence of spatial dependency or spatial correlation in input data over space.
Spatial statistics: A generalization of traditional statistics for spatial data that makes it possible to model spatial dependency and heterogeneity.
Spatial data mining: A generalization of traditional data mining that explores the trade-offs between computational scalability and mathematical rigor, for spatial data.
The remarkable growth in location-aware data (e.g., GPS tracks of smart phones, remotely sensed satellite imagery) and recent advances in computer infrastructure highlight the need for automated systems to discover spatial patterns in the data. Spatial data mining (SDM) is the process of discovering non-trivial, interesting and previously unknown, but potentially useful patterns from large spatial and spatio-temporal databases (Han and Miller 2009, Shekhar et al. 2015b; Xie et al. 2017; Shekhar and Vold 2020 ). Given a geospatial dataset, the three key steps for detecting spatial patterns are as follows: 1) pre-processing data to correct noise, error, and missing information along with space-time analysis to identify underlying spatial or spatio-temporal distribution, 2) applying a relevant SDM algorithm to the pre-processed data to produce an output pattern, 3) post-processing the output pattern, and then 4) having domain experts analyze the output to identify novel insights. Further refinement of the SDM algorithm may be needed based on the interpretation of results in the last step.
SDM techniques are crucial to large organizations that make decisions and policies based on large spatial data sets. Table 1 lists some of the domains and relevant SDM applications. For example in ecology and environmental management, scientists classify remote sensing images to classes (e.g., vegetation, wetland, etc.) on a land-cover map. In public safety, the discovery of crime hotspots events may help police departments to allocate resources effectively. Also, in climate science, finding the effects of distant locations on the temperature of a given location can lead to a more accurate temperature estimates.
Table 1: Examples of application domains of spatial data mining
Domain
Spatial data mining application
Public Safety
Discovery of hotspot patterns from crime event maps
Epidemiology
Detection of disease outbreak
Business
Market allocation to maximize stores' profits
Neuroscience
Discovering patterns of human brain activity from neuroimages
Climate Science
Finding positive or negative correlations between temperatures of distance places
The data inputs of SDM include spatial attributes such as latitude, longitude, and elevation, which are used to define the spatial location and extent of spatial objects. Spatial objects include extended objects such as points, lines, and polygons. The spatial relationships among objects are a vital and rich source of information that can enhance feature selection for improving the performance of traditional methods. Further, traditional data mining and machine learning techniques may miss patterns or may yield spurious patterns that have a high-cost (e.g., stigmatization). This is due to the nature of spatial data (e.g., spatial autocorrelation and spatial heterogeneity) that violates classical assumption in statistics, a common problem in data mining and machine learning techniques. The sensitivity of statistical methods to space partitioning and non-stationarity of spatial data along time and space are other key characteristics and challenges of spatial data (Karpatne et al. 2017).
Spatial statistics and spatial data mining are overlapping fields which support each other in many aspects. Spatial statistics have explored many test statistics that can inform the design of spatial data mining approaches. Statistical techniques possess a high mathematical rigor however, computational scalability is not a primary consideration. In contrast, SDM techniques explicitly address a trade-off between mathematical rigor and computational scalability to analysis spatial big data. Figure 1 illustrates the trade-off between spatial statistics, data mining, and spatial data mining. We will detail it further in section 4.
Figure 1. An illustrative example of the trade-off between spatial statistics, spatial data mining, and traditional data mining techniques. Source: authors.
Scope: This article aims to highlight the difference between spatial data mining, traditional data mining, and spatial pattern families. However, we do not discuss spatial statistics and related mathematics in detail. Further, the detailed description of traditional data mining techniques falls outside the scope of this article interested audience can refer to (Tan, Steinbach, and Kumar 2016) as a comprehensive guide in those topics. Another key sub-field in spatial data mining is trajectory data mining, and the detailed description of trajectory data mining techniques falls outside the scope of this article. Interested readers can refer to Zheng (2015) which provides a comprehensive survey on trajectory data mining. Finally, spatial data mining is widely applied to many disciplines (e.g., remote sensing, geography) and related domains (e.g., public health, landscape architecture, urban studies,), the descriptions of which are beyond the scope of this article. Organization: The article is organized as follows. Section 2 provides a brief background on spatial statistics. Section 3 explains four important pattern families, its related applications, and statistical methods. In Section 4, a short highlight of the difference between spatial statistics and spatial data mining followed by future research and trends are provided.
Spatial statistics (Cressie 2015, Gelfand 2010) adheres to the properties spatial auto-correlation and heterogeneity. This differs from traditional statistics which presumes independent and identical distribution (i.i.d) of sample data for their calculations. The i.i.d assumption is the foundation of the majority of data mining methods and statistics theorems. It is the basis for well-known methods such as the maximum likelihood estimation and the central limit theorem. The dependency of spatial data is a well-known fact that is considered as the first law of geography: “Everything is related to everything else, but nearby things are more related than distant things”.
Spatial statistics is sensitive to space partitioning and the values depend on the shape and scale of the partitions. This concept is formally referred to as the modifiable areal unit problem (MAUP). It is also referred to as the multi-scale effect. For example, results can differ when aggregated on states versus household level. Gerrymandering of election districts is another prominent example of MAUP where political parties redraw the boundaries of districts to improve their possibility of winning. Figure 2 shows an example of gerrymandering where a population of 15 that supports candidate A and a population of 10 that supports candidate B are to be partitioned into 5 congressional districts. Only one partition scheme is fair (Figure 2c). In the other schemes gerrymandering gives an unfair advantages to majority of the party (Figure 2b) or the minority party (Figure 2d).
Figure 2. Example of gerrymandering. (a)Base data; (b) Horizontal partitioning, A takes all seats, 5A - 0B; (c) Vertical partitioning, 3A - 2B; (d) Partitioning helping minority B get majority of seats, 2A - 3B. Source: authors.
The following example shows that choosing a proper spatial model is critically important in SDM. In Figure 3a, there are three types of points, squares , circles and triangles . Each point type has two instances. For calculating the spatial correlation between the different points, we partition the space, as shown in Figure 3b and 3c. The spatial distribution of each point type is a feature vector that corresponds to its count in each partition. As shown in Table 2a, based on region partitioning (e.g., Figure 3b and Figure 3c), Pearson’s correlations and support between and are varied. The correlation between triangles and circles in Figure 3b is negative, but the correlation between triangles and circles in Figure 3b is positive. On the other hand, region partitioning in Figure 3c indicates the opposite results in comparison with Figure 3b. Therefore, the results and spatial relationships are varied based on how the study area is partitioned. The spatial relationship between circles and triangles and circles and squares are lost due to different partitioning, as shown in Figure 3b and 3c, respectively. By contrast, Figure 3d shows that a participation index (Table 2b) is able to accurately capture the adjacency.
Figure 3. Examples of spatial statistics. Source: authors.
Table 2. Pearson’s correlation coefficient for region partitioning and a participation index for a neighborhood graph. Results show that the partitioning breaks spatial relationships, whereas the neighborhood graph preserves the relationship.
Methods in spatial statistics (Waller and Gotway 2004) can be categorized based on the type of input data as follows: 1) geostatistics for point referenced data, 2) lattice statistics for areal data, and 3) spatial point processes for spatial point patterns.
Geostatistics. Geostatistics analyzes spatial continuity and weak stationarity (Cressie 2015), which are inherent features of spatial data sets. Geostatistical techniques rely on statistical models that use random variables to model the uncertainty. Geostatistics offers a range of statistical tools, such as kriging, for interpolating the value of a random field at the unsampled locations.
Lattice statistics: A lattice is a model for determining the discrete areas in a spatial distribution. It is a restricted number of grids in a spatial domain. A W-matrix is used to transform the original continuous data into a discretized representation based on spatial neighborhood relationships (Shekhar et al. 2011).
Point process: A point process is a statistical method for generating a point distribution. It determines the probability of a point being located at a location in the study area. A homogeneous Poisson distribution (e.g., Figure 4a) has identical probability across all locations, which is often used as a null hypothesis. Two other assumptions for generating the location of a set of points are, clustered (Figure 4b) and de-clustered (Figure 4c).
Figures 4a-4c. Examples set of points under three different statistical assumptions. Left/a: Complete Spatial Randomness (CSR); Center/b: Clustered; Right/c: De-clustered / uniform. Source: authors.
Spatial data mining methods are designed to detect spatial patterns (Shekhar et al. 2011). We focus on four important pattern families, namely, hotspots, collocations, spatial predictions, and spatial outliers. These pattern families are widely applied in many societally relevant domains such as epidemiology, criminology, traffic safety, ecology, environmental science, climate science, urban planning, etc.
3.1 Hotspot Detection
Given a set of geospatial points which are related to an activity in a spatial domain, hotspots are the regions that are more active and have higher density of points compared to other regions. John Snow’s work in 1854 was an early path breaking example of spatial hotspot detection, where he successfully identified the source of a cholera outbreak. He found that the highest incidence of disease was in proximity to the Broad street water pump (see Figure 5a). This is an illustrative example that shows the importance of hotspot detection in epidemiology domain. However, it must be noted that the notion of a hotspot is domain specific and hotspot detection techniques should consider domain knowledge to model hotspot regions correctly and effectively. For example, hotspots are typically modeled as circular areas in epidemiology or as paths in traffic engineering (Tang, et al. 2017).
Given widespread applications of hotspot detection, software suites have been developed to detect hotspots in spatial and spatio-temporal data sets. SatScan is one of the most prominent free software used for hotspot detection (Kulldorff n.d.). It relies on hypothesis testing for candidate hotspots which are discovered by a cylindrical scanning of the space. The null hypothesis is based on complete spatial randomness (CSR). The alternative hypothesis states that events are more dense inside the cylinder than outside. A candidate is considered statistically significant, if it has the highest log-likelihood ratio amongst all the candidate hotspots (see figure 5b).
Figure 5a-5b. Analysis of water pump site and deaths from cholera in London in 1854. Source: authors.
3.2 Collocation Detection
Spatial collocation patterns (Mohan et al. 2012) represent subsets of features whose instances are located near one another. For example, the symbiotic relationship between the Nile crocodile and Egyptian plover bird exhibits a collocation pattern. Many biological dependencies exhibit collocation patterns. Figure 6a illustrates the spatial distribution detected via a collocation algorithm of instances of five features, namely, plover, crocodile, green trees, dry trees, and wildfire. Similar analysis on crime datasets has shown the collocation of bars with street fights.
Figure 6. Example of detection of collocation patterns. Source: authors.
To measure the degree of clustering in a point distribution, we can use Ripley’s K function (section 4). It is based on an average number of points whose distance is smaller than a predefined threshold from any chosen point. The null hypothesis of Ripley’s K also relies on CSR. The cross-K function extends Ripley’s K function to cases when there are multiple features. It is a spatial statistical method to detect collocation patterns between features of point events. The cross-K function K(h) for binary spatial features is defined as:
[number of j instances within distance h of a randomly-chosen type i instance], (1)
where is the density (number per unit area) of type j instances and h is the distance. Figure 6b shows the cross-K function results for the input represented in Figure 6a. As can be seen, crocodile and plover have high cross-K values which means they are more likely to be located near each other. The low value between green tree and wild fire means that these two are usually located far from each other. Participation index is an upper bound of the cross-K function. It is a popular measure of collocation due to its computational properties (Huang, Shekhar, and Xiong 2004). The index uses a participation ratio, which is another measure for collocation detection. The participation ration of feature in a collocation pattern is the portion of feature engaging in the pattern . Participation index is defined as . In other words, it is the minimum participation ratio of all features engaging in the collocation pattern. Table 2b shows the participation index values for the collocation pattern in Figure 3a. One pattern is which means is 1 because all circles are participating in collocation pattern . Also, two triangles are engaging in collocation pattern which means = . So, , which is the minimum value of the participation ratio of engaged features in the collocation pattern.
3.3 Spatial Prediction
Spatial prediction, also known as spatial classification and regression, is used to identify the relationship between variables in different datasets. These variables are of two types: explanatory variables (i.e., explanatory attributes or features), and a target variable (also known as, dependent variable). If the target variable is discrete, the problem is known as spatial classification. However, when target variables are continuous, the problem is termed as spatial regression. The goal spatial prediction is to predict the value of target variables from explanatory variables using training samples of data and the neighborhood relationships among the locations.
Traditional data mining and machine learning techniques do not generalize well to spatial prediction and often perform poorly (Jiang et al. 2015). For example, in Figure 7b, a decision tree is used to classify wetland and dry land using spectral features from a satellite image shown in Figure 7a. Compared to the ground truth in Figure 7c, the output of the decision tree contains a large amount of “salt-and- pepper” error. Spatial prediction requires the methods that can handle spatial autocorrelation and heterogeneity (Alstadt and Getis 2006; Jiang et al. 2015).
Figure 7a-7c. Example of a spatial classification problem. Left/a: input high-resolution aerial imagery; Center/b: decision tree prediction with salt-and-pepper errors highlighted in white circle; Right/c: map of ground truth: red is dry land, green is wetland. Source: authors.
The spatial auto-regressive (SAR) model is a supervised learning technique that belongs to the family of spatial regression models. It uses the spatial relationship between explanatory features to predict target variables. A neighborhood relationship is necessary for modeling the spatial relationship of explanatory features and it is usually an additional input to SAR. The SAR model is defined as follows:
(2)
where is an adjacency matrix, and models the effect of neighborhood in addition to the effects of selected features and target variable . Parameters and can be learned using Equation 2. Notice that linear regression, which follows the i.i.d assumption, is a special case of the SAR model when is zero. Therefore, the SAR model is more general compared to linear regression model.
For modeling the spatial heterogeneity, we can use a non-parametric technique known as Geographically Weighted Regression (GWR). GWR does not perform regression on all data samples. Instead, it relies on a kernel size configuration where it calculates a local weighted average using neighborhood samples that are within the same bandwidth (e.g., search window) as the current data location (focal point). Samples that are closer to the current location in the search window will get more weight.
To address spatial autocorrelation in aerial imagery, we can use Convolutional Neural Networks (CNN) which perform convolutions using neighborhood data (Cecotti et al. 2020). However, they may not address spatial variability. Thus, spatial variability aware neural networks (SVANN) have been proposed which take distance into account while training neural networks (Gupta, Xie, and Shekhar 2020). In SVANN each parameter is a map, i.e., a function of a location. SVANN has two alternatives for prediction. Zone-based prediction uses the local neural networks for the zone at hand for prediction. The second approach is to combine the predictions from all local neural networks, and favoring the nearby models using distance weighting.
3.4 Spatial Outlier Detection
Outliers may be global or spatial. Global outliers are data samples that are inconsistent with the rest of the data samples, such as credit card fraud. In contrast, spatial outliers differ from other data only in their neighborhood (Shekhar et al. 2011). For example, a new house surrounded by older houses in a developed city can be considered a spatial outlier, but it may not be a global outlier based on the overall age of houses in the city. In another example, Figure 8 shows the 1992 United States presidential election results for all 50 states. Indiana is the spatial outlier in this example. Spatial outlier detection is vital for applications that need to find an unusual or suspicious activity or objects compared to their neighborhoods.
Figure 8. State-level United States presidential election results from 1992. Indiana is a spatial outlier. Source: authors.
There are two classes of statistical tests for detecting spatial outliers, graphical tests, and quantitative tests. Graphical tests detect outliers via analyzing visualized patterns from data. Examples include Variogram clouds and Moran scatter plots. Quantitative tests calculate the difference between non-spatial attributes of inspected points and their spatial neighbors. When the difference is larger than a predefined threshold, an outlier is detected. Neighborhood spatial statistics and scatterplots are quantitative tests.
Spatial statistics and spatial data mining overlap as shown in Figure 9. Spatial statistical techniques (e.g., Spatial Scan Statistic and Ripley’s K function) are mathematically rigorous which can eliminate chance patterns and evaluates the robustness of an output from a spatial pattern mining algorithm. However, a key challenge in such techniques is computational scalability when using spatial big data that contains thousands of point features that grow exponentially. This highlights the limitations of spatial statistics which are potentially addressed in spatial data mining (SDM). For example, in collocation detection, participation index (Huang, Shekhar, and Xiong 2004) is introduced that defines an upper- bound on the cross-K function such that index decreases monotonically as the size of the collocation pattern increases (Xie et al. 2017). The upper bound allows to limit the collocation search space providing a computationally feasible algorithms to detect collocation patterns.
Figure 9. An illustrative Venn diagram to highlight the spatial statistics and spatial data mining concepts described in this article. Source: authors.
Most research in spatial data mining assumes 1) that space is Euclidean and isometric (i.e., it has the same statistical properties along different directions), and 2) that neighborhoods are symmetric. However, in many applications, space is a network space. For example, road networks and river networks can be modeled by network space more effectively. Considering network structure is one of the challenges of using network space, but research in this area promises to provide more accurate insights.
In addition to the space dimension, the temporal dimension is another crucial aspect of spatial data. Useful information and patterns can often be identified by adding a temporal dimension to SDM techniques. Detection of the time point that impacts some phenomenon is a key problem, which is called change detection. For example, change detection helps to detect when climate change has occurred in a region such that appropriate protective action can be taken in that region. In a teleconnection discovery problem, we have collection of spatial time series of different locations. Teleconnection discovery aims to find pairs of positively or negatively correlated points of time series at great distance. Teleconnection discovery is used in climate science to more accurately predict temperatures of different places in the world. Adding the time dimension to SDM problems will likely open new and more complex statistical, mathematical, and computational models that can address grand societal challenges.
Finally, domain experts provide a rich source of information to enhance data-driven spatial models. Simulation models usually integrate physical rules and related domain knowledge into the data mining models to gain new and useful insights (Karpatne et al. 2017). Simulation models are usually complicated from a computational perspective. Consequently, new data science approaches are needed that implement fast approximate solutions of simulation models. Due to potentially high cost of spurious patterns in societal applications (e.g., crime pattern analysis, disease outbreaks), it is important that new techniques are statistically robust.
References:
Aldstadt, J. and Getis, A. (2006). Using AMOEBA to create a spatial weights matrix and identify spatial clusters. Geographical Analysis 38 (4): 327–343.
Cecotti, H., Rivera, A, Farhadloo, M., and Villarreal, M. (2020). Grape detection with Convolutional Neural Networks. Expert Systems with Applications 159 (113588). DOI: 10.1016/j.eswa.2020.113588.
Cressie, N. (2015). Statistics for spatial data. John Wiley & Sons.
Gelfand, A. E., Diggle, P., Guttrop, P., and Fuentes, M. (2010). Handbook of Spatial Statistics. CRC Press.
Gupta, J., Xie, Y., and Shekhar, S. (2020). “Towards Spatial Variability Aware Deep Neural Networks (SVANN): A Summary of Results”. In: DeepSpatial2020, 1st ACM SIGKDD Workshop on Deep Learning for Spatiotemporal Data, Applications, and Systems.
Han, J. and Miller, H. J. (2009). Geographic data mining and knowledge discovery. CRC Press.
Huang, Y., Shekhar, S. and Xiong, H. (2004). Discovering colocation patterns from spatial data sets: a general approach. IEEE Transactions on Knowledge and Data Engineering 16(12):1472–1485.
Jiang, Z., Shekhar, S., Zhou, X., Knight, J., and Corcoran, J. (2015). Focal-test-based spatial decision tree learning. IEEE Transactions on Knowledge and Data Engineering 27(6):1547– 1559.
Karpatne, A., Alturi, G., Faghmous, J. H., Steinbach, M., Banerjee, A., Ganguly, A., Shekhar, S., Samatova, N., and Kumar, V. (2017). Theory-guided data science: A new paradigm for scientific discovery from data. IEEE Transactions on Knowledge and Data Engineering 29(10): 2318–2331.
Kulldorff, M. (n.d.) SaTScanTM user guide, www. satscan. org .
Mohan, P., Shekhar, S., Shine, J. A., and Rogers, J. P. (2012). Cascading spatio-temporal pattern discovery. IEEE Transactions on Knowledge and Data Engineering 24(11):1977–1992.
Shekhar, S., Feiner, S. K., and Aref, W. G. (2015a). Spatial computing. Communications of the ACM. 59(1):72–81.
Shekhar, S., Evans, M. R., Kang, J. M., and Mohan, P. (2011). Identifying patterns in spatial information: A survey of methods. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 1(3):193–214.
Shekhar, S., Jiang, Z., Ali, R., Eftelioglu, E., Tang, X., Gunturi, V. M. V., an Zhou, X. (2015b). Spatiotemporal data mining: a computational perspective. ISPRS International Journal of Geo-Information 4(4): 2306– 2338.
Shekhar, S., and Vold, P. (2020). Spatial Computing. The MIT Press Essential Knowledge series. Cambridge, MA: The MIT Press.
Shekhar, S., Xiong, H., and Zhou, X. (Eds.) (2017). Encyclopedia of GIS, 2nd edition. Springer International Publishing.
Tan, P.-N., Steinbach, M., and Kumar, V. (2006). Introduction to Data Mining, 1st Edition. Pearson.
Tang, X., Eftelioglu, E., Oliver, D., and Shekhar, S. (2017). Significant Linear Hotspot Discovery. IEEE Transactions on Big Data 3(2): 140–153.
Waller, L. A. and Gotway, C. A. (2004). Applied Spatial Statistics for Public Health Data. John Wiley & Sons. DOI: 10.1002/0471662682.
Xie, Y., Eftelioglu, E., Ali, R., Tang, X., Li, Yl, Doshi, R., and Shekhar, S. (2017). Transdisciplinary Foundations of Geospatial Data Science. ISPRS International Journal of Geo-Information 6(12): 395. DOI: 10.3390/ijgi6120395
Zheng, Y. (2015). Trajectory data mining: an overview. ACM Transactions on Intelligent Systems and Technology (TIST). 6(3): 1–41. DOI: 10.1145/2743025
Learning Objectives:
Explain the i.i.d assumption and illustrate why it not valid for spatial data
Describe the following two key concepts in spatial statistics: spatial autocorrelation and spatial heterogeneity
Define MAUP and explain gerrymandering as an example of MAUP
List three areas of spatial statistics and briefly explain them
Name five spatial patterns and illustrate them
Instructional Assessment Questions:
Which statement(s) violate the independence assumption?
Mohamed Lee” is a rare name, even though “Mohamed” is the most frequent first name and “Lee” is the most frequent last name.
Near things are more related than distant things.
Nearby video frames often show common people and objects.
All of the above
Which of the three images in Figure 10 (below) exhibits the highest spatial autocorrelation?
image 10a
image 10b
image 10c
Which statement(s) violate the identical distribution assumption underlying traditional statistical methods?
Cancer cell heterogeneity makes treatment of cancer difficult.
No two places on Earth are exactly alike.
All politics is local.
All of the above
Which of the following are properties of spatial data?
Autocorrelation
Heterogeneity
Implicit relationships (e.g., neighbor)
All of the above
Which of the following is not attributed to spatial auto-correlation?
Nearby cities have similar climate.
Neighboring areas tend to plant similar farm crops.
Near things are more related than distant things.
Spatial data mining results are less reliable near the edges of a study area.
Which of the following is correct about gerrymandering:
It is about redrawing boundaries of districts.
It can help a party or group to take a political advantage.
It can change the result of an election in a way which contradicts the popular vote.
All of the above
Spatial pattern families include hotspots, colocations, location predictions, and spatial outliers. Which pattern does each question below correspond to?
Which countries are very different from their neighbors?
Which highway-segments have abnormally high accident rates ?
Where will a hurricane that’s brewing over the ocean make landfall?
Which retail-store-types often co-locate in shopping malls?
Which does not illustrate a spatial-hotspot pattern family?
Roads with an unusually high rate of traffic accidents.
Areas with an unusually high concentration of museums.
Cities with unusually high numbers of students enrolled in a particular massive open online course (MOOC).
A neighborhood with an unusually high rate of an infectious disease (or crime).
Which does not illustrate colocation?
A loud sound temporally follows a bright flash of lightning.
Nuclear power plants are usually located near water.
Egyptian plover birds live close to Nile crocodiles.
College campuses often have bookstores nearby.
Which of the following is false about spatial outliers?
An oasis (isolated area of vegetation) is a spatial outlier area in a desert.
A spatial outlier may reveal discontinuities and abrupt changes.
A spatial outlier is significantly different from their spatial neighbors.
A spatial outlier is significantly different from the population as a whole.
Additional Resources:
A series of 8 short videos on spatial data mining, shared by Spatial Computing. Collection can be found here online.
You are currently viewing an archived version of Topic An Introduction to Spatial Data Mining. If updates or revisions have been published you can find them at An Introduction to Spatial Data Mining.
The goal of spatial data mining is to discover potentially useful, interesting, and non-trivial patterns from spatial data-sets (e.g., GPS trajectory of smartphones). Spatial data mining is societally important having applications in public health, public safety, climate science, etc. For example, in epidemiology, spatial data mining helps to nd areas with a high concentration of disease incidents to manage disease outbreaks. Computational methods are needed to discover spatial patterns since the volume and velocity of spatial data exceed the ability of human experts to analyze it. Spatial data has unique characteristics like spatial autocorrelation and spatial heterogeneity which violate the i.i.d (Independent and Identically Distributed) assumption of traditional statistic and data mining methods. Therefore, using traditional methods may miss patterns or may yield spurious patterns, which are costly in societal applications. Further, there are additional challenges such as MAUP (Modiable Areal Unit Problem) as illustrated by a recent court case debating gerrymandering in elections. In this article, we discuss tools and computational methods of spatial data mining, focusing on the primary spatial pattern families: hotspot detection, collocation detection, spatial prediction, and spatial outlier detection. Hotspot detection methods use domain information to accurately model more active and high-density areas. Collocation detection methods find objects whose instances are in proximity to each other in a location. Spatial prediction approaches explicitly model the neighborhood relationship of locations to predict target variables from input features. Finally, spatial outlier detection methods find data that differ from their neighbors. Lastly, we describe future research and trends in spatial data mining.
Golmohammadi, J., Xie, Y., Gupta, J., Farhadloo, M., Li, Y., Cai, J., Detor, S., Roh, A., Shekhar, S. (2020). An Introduction to Spatial Data Mining. The Geographic Information Science & Technology Body of Knowledge (4th Quarter 2020 Edition), John P. Wilson (Ed.). DOI:10.22224/gistbok/2020.4.5..
This entry was first published on November 20, 2020. No earlier editions exist.
This article is supported by National Science Foundation under Grant No.1541876, 1029711, 1737633, IIS-1320580 , IIS-0940818, and IIS-1218168 , the USDOD under Grants No.HM1582-08-1-0017 and HM0210-13-1-0005, the Advanced Research Projects Agency-Energy (ARPA-E), U.S. Department of Energy under Award No.DE-AR0000795, the NIH under Grant No. UL1 TR002494, KL2TR002492, and TL1 TR002493, the USDA under Grant No.2017-51181-27222, and the OVPR Infrastructure Investment Initiative, Minnesota Supercomputing Institute (MSI), and Provost’s Grand Challenges Exploratory Research and International Enhancements Grants at the University of Minnesota. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. Also, we appreciate Kim Koffolt’s helpful comments and feedbacks for enhancing readability of the paper.
1. Definitions
Spatial data: Any data that includes location information such as street address, or longitude and latitude.
Independent and Identically Distributed (i.i.d) assumption: A classical assumption in statistics that presumes data samples to be independent of each other and are distributed identically.
Spatial autocorrelation: It is defined as a measure of dependency among points in a spatial neighborhood. The dependency of spatial data rejects the independence assumption of classical statistics.
Spatial heterogeneity (or spatial non-stationarity): It refers to the variation in events, features and relationships across a region. It violates the assumption of identical distribution.
Spatial continuity: It refers to the presence of spatial dependency or spatial correlation in input data over space.
Spatial statistics: A generalization of traditional statistics for spatial data that makes it possible to model spatial dependency and heterogeneity.
Spatial data mining: A generalization of traditional data mining that explores the trade-offs between computational scalability and mathematical rigor, for spatial data.
2. Introduction
The remarkable growth in location-aware data (e.g., GPS tracks of smart phones, remotely sensed satellite imagery) and recent advances in computer infrastructure highlight the need for automated systems to discover spatial patterns in the data. Spatial data mining (SDM) is the process of discovering non-trivial, interesting and previously unknown, but potentially useful patterns from large spatial and spatio-temporal databases (Han and Miller 2009, Shekhar et al. 2015b; Xie et al. 2017; Shekhar and Vold 2020 ). Given a geospatial dataset, the three key steps for detecting spatial patterns are as follows: 1) pre-processing data to correct noise, error, and missing information along with space-time analysis to identify underlying spatial or spatio-temporal distribution, 2) applying a relevant SDM algorithm to the pre-processed data to produce an output pattern, 3) post-processing the output pattern, and then 4) having domain experts analyze the output to identify novel insights. Further refinement of the SDM algorithm may be needed based on the interpretation of results in the last step.
SDM techniques are crucial to large organizations that make decisions and policies based on large spatial data sets. Table 1 lists some of the domains and relevant SDM applications. For example in ecology and environmental management, scientists classify remote sensing images to classes (e.g., vegetation, wetland, etc.) on a land-cover map. In public safety, the discovery of crime hotspots events may help police departments to allocate resources effectively. Also, in climate science, finding the effects of distant locations on the temperature of a given location can lead to a more accurate temperature estimates.
The data inputs of SDM include spatial attributes such as latitude, longitude, and elevation, which are used to define the spatial location and extent of spatial objects. Spatial objects include extended objects such as points, lines, and polygons. The spatial relationships among objects are a vital and rich source of information that can enhance feature selection for improving the performance of traditional methods. Further, traditional data mining and machine learning techniques may miss patterns or may yield spurious patterns that have a high-cost (e.g., stigmatization). This is due to the nature of spatial data (e.g., spatial autocorrelation and spatial heterogeneity) that violates classical assumption in statistics, a common problem in data mining and machine learning techniques. The sensitivity of statistical methods to space partitioning and non-stationarity of spatial data along time and space are other key characteristics and challenges of spatial data (Karpatne et al. 2017).
Spatial statistics and spatial data mining are overlapping fields which support each other in many aspects. Spatial statistics have explored many test statistics that can inform the design of spatial data mining approaches. Statistical techniques possess a high mathematical rigor however, computational scalability is not a primary consideration. In contrast, SDM techniques explicitly address a trade-off between mathematical rigor and computational scalability to analysis spatial big data. Figure 1 illustrates the trade-off between spatial statistics, data mining, and spatial data mining. We will detail it further in section 4.
Figure 1. An illustrative example of the trade-off between spatial statistics, spatial data mining, and traditional data mining techniques. Source: authors.
Scope: This article aims to highlight the difference between spatial data mining, traditional data mining, and spatial pattern families. However, we do not discuss spatial statistics and related mathematics in detail. Further, the detailed description of traditional data mining techniques falls outside the scope of this article interested audience can refer to (Tan, Steinbach, and Kumar 2016) as a comprehensive guide in those topics. Another key sub-field in spatial data mining is trajectory data mining, and the detailed description of trajectory data mining techniques falls outside the scope of this article. Interested readers can refer to Zheng (2015) which provides a comprehensive survey on trajectory data mining. Finally, spatial data mining is widely applied to many disciplines (e.g., remote sensing, geography) and related domains (e.g., public health, landscape architecture, urban studies,), the descriptions of which are beyond the scope of this article.
Organization: The article is organized as follows. Section 2 provides a brief background on spatial statistics. Section 3 explains four important pattern families, its related applications, and statistical methods. In Section 4, a short highlight of the difference between spatial statistics and spatial data mining followed by future research and trends are provided.
2. Spatial Statistics
Spatial statistics (Cressie 2015, Gelfand 2010) adheres to the properties spatial auto-correlation and heterogeneity. This differs from traditional statistics which presumes independent and identical distribution (i.i.d) of sample data for their calculations. The i.i.d assumption is the foundation of the majority of data mining methods and statistics theorems. It is the basis for well-known methods such as the maximum likelihood estimation and the central limit theorem. The dependency of spatial data is a well-known fact that is considered as the first law of geography: “Everything is related to everything else, but nearby things are more related than distant things”.
Spatial statistics is sensitive to space partitioning and the values depend on the shape and scale of the partitions. This concept is formally referred to as the modifiable areal unit problem (MAUP). It is also referred to as the multi-scale effect. For example, results can differ when aggregated on states versus household level. Gerrymandering of election districts is another prominent example of MAUP where political parties redraw the boundaries of districts to improve their possibility of winning. Figure 2 shows an example of gerrymandering where a population of 15 that supports candidate A and a population of 10 that supports candidate B are to be partitioned into 5 congressional districts. Only one partition scheme is fair (Figure 2c). In the other schemes gerrymandering gives an unfair advantages to majority of the party (Figure 2b) or the minority party (Figure 2d).
Figure 2. Example of gerrymandering. (a)Base data; (b) Horizontal partitioning, A takes all seats, 5A - 0B; (c) Vertical partitioning, 3A - 2B; (d) Partitioning helping minority B get majority of seats, 2A - 3B. Source: authors.
The following example shows that choosing a proper spatial model is critically important in SDM. In Figure 3a, there are three types of points, squares , circles
, circles  and triangles
and triangles 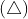 . Each point type has two instances. For calculating the spatial correlation between the different points, we partition the space, as shown in Figure 3b and 3c. The spatial distribution of each point type is a feature vector that corresponds to its count in each partition. As shown in Table 2a, based on region partitioning (e.g., Figure 3b and Figure 3c), Pearson’s correlations and support between
. Each point type has two instances. For calculating the spatial correlation between the different points, we partition the space, as shown in Figure 3b and 3c. The spatial distribution of each point type is a feature vector that corresponds to its count in each partition. As shown in Table 2a, based on region partitioning (e.g., Figure 3b and Figure 3c), Pearson’s correlations and support between 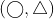 and
and 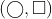 are varied. The correlation between triangles and circles in Figure 3b is negative, but the correlation between triangles and circles in Figure 3b is positive. On the other hand, region partitioning in Figure 3c indicates the opposite results in comparison with Figure 3b. Therefore, the results and spatial relationships are varied based on how the study area is partitioned. The spatial relationship between circles and triangles and circles and squares are lost due to different partitioning, as shown in Figure 3b and 3c, respectively. By contrast, Figure 3d shows that a participation index (Table 2b) is able to accurately capture the adjacency.
are varied. The correlation between triangles and circles in Figure 3b is negative, but the correlation between triangles and circles in Figure 3b is positive. On the other hand, region partitioning in Figure 3c indicates the opposite results in comparison with Figure 3b. Therefore, the results and spatial relationships are varied based on how the study area is partitioned. The spatial relationship between circles and triangles and circles and squares are lost due to different partitioning, as shown in Figure 3b and 3c, respectively. By contrast, Figure 3d shows that a participation index (Table 2b) is able to accurately capture the adjacency.
Figure 3. Examples of spatial statistics. Source: authors.
Table 2. Pearson’s correlation coefficient for region partitioning and a participation index for a neighborhood graph. Results show that the partitioning breaks spatial relationships, whereas the neighborhood graph preserves the relationship.
Methods in spatial statistics (Waller and Gotway 2004) can be categorized based on the type of input data as follows: 1) geostatistics for point referenced data, 2) lattice statistics for areal data, and 3) spatial point processes for spatial point patterns.
Figures 4a-4c. Examples set of points under three different statistical assumptions. Left/a: Complete Spatial Randomness (CSR); Center/b: Clustered; Right/c: De-clustered / uniform. Source: authors.
3. Spatial Pattern Families
Spatial data mining methods are designed to detect spatial patterns (Shekhar et al. 2011). We focus on four important pattern families, namely, hotspots, collocations, spatial predictions, and spatial outliers. These pattern families are widely applied in many societally relevant domains such as epidemiology, criminology, traffic safety, ecology, environmental science, climate science, urban planning, etc.
3.1 Hotspot Detection
Given a set of geospatial points which are related to an activity in a spatial domain, hotspots are the regions that are more active and have higher density of points compared to other regions. John Snow’s work in 1854 was an early path breaking example of spatial hotspot detection, where he successfully identified the source of a cholera outbreak. He found that the highest incidence of disease was in proximity to the Broad street water pump (see Figure 5a). This is an illustrative example that shows the importance of hotspot detection in epidemiology domain. However, it must be noted that the notion of a hotspot is domain specific and hotspot detection techniques should consider domain knowledge to model hotspot regions correctly and effectively. For example, hotspots are typically modeled as circular areas in epidemiology or as paths in traffic engineering (Tang, et al. 2017).
Given widespread applications of hotspot detection, software suites have been developed to detect hotspots in spatial and spatio-temporal data sets. SatScan is one of the most prominent free software used for hotspot detection (Kulldorff n.d.). It relies on hypothesis testing for candidate hotspots which are discovered by a cylindrical scanning of the space. The null hypothesis is based on complete spatial randomness (CSR). The alternative hypothesis states that events are more dense inside the cylinder than outside. A candidate is considered statistically significant, if it has the highest log-likelihood ratio amongst all the candidate hotspots (see figure 5b).
Figure 5a-5b. Analysis of water pump site and deaths from cholera in London in 1854. Source: authors.
3.2 Collocation Detection
Spatial collocation patterns (Mohan et al. 2012) represent subsets of features whose instances are located near one another. For example, the symbiotic relationship between the Nile crocodile and Egyptian plover bird exhibits a collocation pattern. Many biological dependencies exhibit collocation patterns. Figure 6a illustrates the spatial distribution detected via a collocation algorithm of instances of five features, namely, plover, crocodile, green trees, dry trees, and wildfire. Similar analysis on crime datasets has shown the collocation of bars with street fights.
Figure 6. Example of detection of collocation patterns. Source: authors.
To measure the degree of clustering in a point distribution, we can use Ripley’s K function (section 4). It is based on an average number of points whose distance is smaller than a predefined threshold from any chosen point. The null hypothesis of Ripley’s K also relies on CSR. The cross-K function extends Ripley’s K function to cases when there are multiple features. It is a spatial statistical method to detect collocation patterns between features of point events. The cross-K function K(h) for binary spatial features is defined as:
where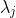 is the density (number per unit area) of type j instances and h is the distance. Figure 6b shows the cross-K function results for the input represented in Figure 6a. As can be seen, crocodile and plover have high cross-K values which means they are more likely to be located near each other. The low value between green tree and wild fire means that these two are usually located far from each other. Participation index is an upper bound of the cross-K function. It is a popular measure of collocation due to its computational properties (Huang, Shekhar, and Xiong 2004). The index uses a participation ratio, which is another measure for collocation detection. The participation ration of feature
is the density (number per unit area) of type j instances and h is the distance. Figure 6b shows the cross-K function results for the input represented in Figure 6a. As can be seen, crocodile and plover have high cross-K values which means they are more likely to be located near each other. The low value between green tree and wild fire means that these two are usually located far from each other. Participation index is an upper bound of the cross-K function. It is a popular measure of collocation due to its computational properties (Huang, Shekhar, and Xiong 2004). The index uses a participation ratio, which is another measure for collocation detection. The participation ration of feature 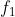 in a collocation pattern
in a collocation pattern 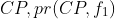 is the portion of feature
is the portion of feature 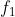 engaging in the pattern
engaging in the pattern 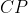 . Participation index is defined as
. Participation index is defined as 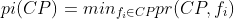 . In other words, it is the minimum participation ratio of all features engaging in the collocation pattern. Table 2b shows the participation index values for the collocation pattern in Figure 3a. One pattern is
. In other words, it is the minimum participation ratio of all features engaging in the collocation pattern. Table 2b shows the participation index values for the collocation pattern in Figure 3a. One pattern is 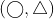 which means
which means 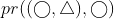 is 1 because all circles are participating in collocation pattern
is 1 because all circles are participating in collocation pattern 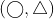 . Also, two triangles are engaging in collocation pattern
. Also, two triangles are engaging in collocation pattern 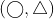 which means
which means 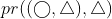 =
= 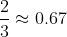 . So,
. So, 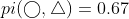 , which is the minimum value of the participation ratio of engaged features in the collocation pattern.
, which is the minimum value of the participation ratio of engaged features in the collocation pattern.
3.3 Spatial Prediction
Spatial prediction, also known as spatial classification and regression, is used to identify the relationship between variables in different datasets. These variables are of two types: explanatory variables (i.e., explanatory attributes or features), and a target variable (also known as, dependent variable). If the target variable is discrete, the problem is known as spatial classification. However, when target variables are continuous, the problem is termed as spatial regression. The goal spatial prediction is to predict the value of target variables from explanatory variables using training samples of data and the neighborhood relationships among the locations.
Traditional data mining and machine learning techniques do not generalize well to spatial prediction and often perform poorly (Jiang et al. 2015). For example, in Figure 7b, a decision tree is used to classify wetland and dry land using spectral features from a satellite image shown in Figure 7a. Compared to the ground truth in Figure 7c, the output of the decision tree contains a large amount of “salt-and- pepper” error. Spatial prediction requires the methods that can handle spatial autocorrelation and heterogeneity (Alstadt and Getis 2006; Jiang et al. 2015).
Figure 7a-7c. Example of a spatial classification problem. Left/a: input high-resolution aerial imagery; Center/b: decision tree prediction with salt-and-pepper errors highlighted in white circle; Right/c: map of ground truth: red is dry land, green is wetland. Source: authors.
The spatial auto-regressive (SAR) model is a supervised learning technique that belongs to the family of spatial regression models. It uses the spatial relationship between explanatory features to predict target variables. A neighborhood relationship is necessary for modeling the spatial relationship of explanatory features and it is usually an additional input to SAR. The SAR model is defined as follows:
where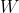 is an adjacency matrix, and
is an adjacency matrix, and 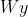 models the effect of neighborhood in addition to the effects of selected features
models the effect of neighborhood in addition to the effects of selected features 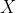 and target variable
and target variable 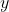 . Parameters
. Parameters  and
and 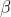 can be learned using Equation 2. Notice that linear regression, which follows the i.i.d assumption, is a special case of the SAR model when
can be learned using Equation 2. Notice that linear regression, which follows the i.i.d assumption, is a special case of the SAR model when  is zero. Therefore, the SAR model is more general compared to linear regression model.
is zero. Therefore, the SAR model is more general compared to linear regression model.
For modeling the spatial heterogeneity, we can use a non-parametric technique known as Geographically Weighted Regression (GWR). GWR does not perform regression on all data samples. Instead, it relies on a kernel size configuration where it calculates a local weighted average using neighborhood samples that are within the same bandwidth (e.g., search window) as the current data location (focal point). Samples that are closer to the current location in the search window will get more weight.
To address spatial autocorrelation in aerial imagery, we can use Convolutional Neural Networks (CNN) which perform convolutions using neighborhood data (Cecotti et al. 2020). However, they may not address spatial variability. Thus, spatial variability aware neural networks (SVANN) have been proposed which take distance into account while training neural networks (Gupta, Xie, and Shekhar 2020). In SVANN each parameter is a map, i.e., a function of a location. SVANN has two alternatives for prediction. Zone-based prediction uses the local neural networks for the zone at hand for prediction. The second approach is to combine the predictions from all local neural networks, and favoring the nearby models using distance weighting.
3.4 Spatial Outlier Detection
Outliers may be global or spatial. Global outliers are data samples that are inconsistent with the rest of the data samples, such as credit card fraud. In contrast, spatial outliers differ from other data only in their neighborhood (Shekhar et al. 2011). For example, a new house surrounded by older houses in a developed city can be considered a spatial outlier, but it may not be a global outlier based on the overall age of houses in the city. In another example, Figure 8 shows the 1992 United States presidential election results for all 50 states. Indiana is the spatial outlier in this example. Spatial outlier detection is vital for applications that need to find an unusual or suspicious activity or objects compared to their neighborhoods.
Figure 8. State-level United States presidential election results from 1992. Indiana is a spatial outlier. Source: authors.
There are two classes of statistical tests for detecting spatial outliers, graphical tests, and quantitative tests. Graphical tests detect outliers via analyzing visualized patterns from data. Examples include Variogram clouds and Moran scatter plots. Quantitative tests calculate the difference between non-spatial attributes of inspected points and their spatial neighbors. When the difference is larger than a predefined threshold, an outlier is detected. Neighborhood spatial statistics and scatterplots are quantitative tests.
4. Discussion and Future Directions
Spatial statistics and spatial data mining overlap as shown in Figure 9. Spatial statistical techniques (e.g., Spatial Scan Statistic and Ripley’s K function) are mathematically rigorous which can eliminate chance patterns and evaluates the robustness of an output from a spatial pattern mining algorithm. However, a key challenge in such techniques is computational scalability when using spatial big data that contains thousands of point features that grow exponentially. This highlights the limitations of spatial statistics which are potentially addressed in spatial data mining (SDM). For example, in collocation detection, participation index (Huang, Shekhar, and Xiong 2004) is introduced that defines an upper- bound on the cross-K function such that index decreases monotonically as the size of the collocation pattern increases (Xie et al. 2017). The upper bound allows to limit the collocation search space providing a computationally feasible algorithms to detect collocation patterns.
Figure 9. An illustrative Venn diagram to highlight the spatial statistics and spatial data mining concepts described in this article. Source: authors.
Most research in spatial data mining assumes 1) that space is Euclidean and isometric (i.e., it has the same statistical properties along different directions), and 2) that neighborhoods are symmetric. However, in many applications, space is a network space. For example, road networks and river networks can be modeled by network space more effectively. Considering network structure is one of the challenges of using network space, but research in this area promises to provide more accurate insights.
In addition to the space dimension, the temporal dimension is another crucial aspect of spatial data. Useful information and patterns can often be identified by adding a temporal dimension to SDM techniques. Detection of the time point that impacts some phenomenon is a key problem, which is called change detection. For example, change detection helps to detect when climate change has occurred in a region such that appropriate protective action can be taken in that region. In a teleconnection discovery problem, we have collection of spatial time series of different locations. Teleconnection discovery aims to find pairs of positively or negatively correlated points of time series at great distance. Teleconnection discovery is used in climate science to more accurately predict temperatures of different places in the world. Adding the time dimension to SDM problems will likely open new and more complex statistical, mathematical, and computational models that can address grand societal challenges.
Finally, domain experts provide a rich source of information to enhance data-driven spatial models. Simulation models usually integrate physical rules and related domain knowledge into the data mining models to gain new and useful insights (Karpatne et al. 2017). Simulation models are usually complicated from a computational perspective. Consequently, new data science approaches are needed that implement fast approximate solutions of simulation models. Due to potentially high cost of spurious patterns in societal applications (e.g., crime pattern analysis, disease outbreaks), it is important that new techniques are statistically robust.
Aldstadt, J. and Getis, A. (2006). Using AMOEBA to create a spatial weights matrix and identify spatial clusters. Geographical Analysis 38 (4): 327–343.
Cecotti, H., Rivera, A, Farhadloo, M., and Villarreal, M. (2020). Grape detection with Convolutional Neural Networks. Expert Systems with Applications 159 (113588). DOI: 10.1016/j.eswa.2020.113588.
Cressie, N. (2015). Statistics for spatial data. John Wiley & Sons.
Gelfand, A. E., Diggle, P., Guttrop, P., and Fuentes, M. (2010). Handbook of Spatial Statistics. CRC Press.
Gupta, J., Xie, Y., and Shekhar, S. (2020). “Towards Spatial Variability Aware Deep Neural Networks (SVANN): A Summary of Results”. In: DeepSpatial2020, 1st ACM SIGKDD Workshop on Deep Learning for Spatiotemporal Data, Applications, and Systems.
Han, J. and Miller, H. J. (2009). Geographic data mining and knowledge discovery. CRC Press.
Huang, Y., Shekhar, S. and Xiong, H. (2004). Discovering colocation patterns from spatial data sets: a general approach. IEEE Transactions on Knowledge and Data Engineering 16(12):1472–1485.
Jiang, Z., Shekhar, S., Zhou, X., Knight, J., and Corcoran, J. (2015). Focal-test-based spatial decision tree learning. IEEE Transactions on Knowledge and Data Engineering 27(6):1547– 1559.
Karpatne, A., Alturi, G., Faghmous, J. H., Steinbach, M., Banerjee, A., Ganguly, A., Shekhar, S., Samatova, N., and Kumar, V. (2017). Theory-guided data science: A new paradigm for scientific discovery from data. IEEE Transactions on Knowledge and Data Engineering 29(10): 2318–2331.
Kulldorff, M. (n.d.) SaTScanTM user guide, www. satscan. org .
Mohan, P., Shekhar, S., Shine, J. A., and Rogers, J. P. (2012). Cascading spatio-temporal pattern discovery. IEEE Transactions on Knowledge and Data Engineering 24(11):1977–1992.
Shekhar, S., Feiner, S. K., and Aref, W. G. (2015a). Spatial computing. Communications of the ACM. 59(1):72–81.
Shekhar, S., Evans, M. R., Kang, J. M., and Mohan, P. (2011). Identifying patterns in spatial information: A survey of methods. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 1(3):193–214.
Shekhar, S., Jiang, Z., Ali, R., Eftelioglu, E., Tang, X., Gunturi, V. M. V., an Zhou, X. (2015b). Spatiotemporal data mining: a computational perspective. ISPRS International Journal of Geo-Information 4(4): 2306– 2338.
Shekhar, S., and Vold, P. (2020). Spatial Computing. The MIT Press Essential Knowledge series. Cambridge, MA: The MIT Press.
Shekhar, S., Xiong, H., and Zhou, X. (Eds.) (2017). Encyclopedia of GIS, 2nd edition. Springer International Publishing.
Tan, P.-N., Steinbach, M., and Kumar, V. (2006). Introduction to Data Mining, 1st Edition. Pearson.
Tang, X., Eftelioglu, E., Oliver, D., and Shekhar, S. (2017). Significant Linear Hotspot Discovery. IEEE Transactions on Big Data 3(2): 140–153.
Waller, L. A. and Gotway, C. A. (2004). Applied Spatial Statistics for Public Health Data. John Wiley & Sons. DOI: 10.1002/0471662682.
Xie, Y., Eftelioglu, E., Ali, R., Tang, X., Li, Yl, Doshi, R., and Shekhar, S. (2017). Transdisciplinary Foundations of Geospatial Data Science. ISPRS International Journal of Geo-Information 6(12): 395. DOI: 10.3390/ijgi6120395
Zheng, Y. (2015). Trajectory data mining: an overview. ACM Transactions on Intelligent Systems and Technology (TIST). 6(3): 1–41. DOI: 10.1145/2743025
Keywords: