In the same manner as distance, direction plays an equally important role in GIS. This article first summarizes different ways of measuring direction, either quantitatively or qualitatively. Formulas and examples are provided. In the following discussion, fundamental differences between distance and direction in describing spatial relations is examined; properties of angles are emphasized in the context of GIS; and the classification of both cardinal and projective direction is illustrated. With a focus on quantitative operations, various directional operations are categorized and elaborated based on factors such as the underlying data model (vector or raster) and whether direction effect is explicitly or implicitly embedded in the data.
Author and Citation Info:
Zhu, R. (2021). Directional Operations. The Geographic Information Science & Technology Body of Knowledge (4th Quarter 2021 Edition), John P. Wilson (ed.). DOI: 10.22224/gistbok/2021.4.2.
This entry is also available in an earlier edition:
DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Distance, Length, and Direction. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital).
Direction: Direction in GIS generally means the position towards which a geographic feature moves or faces. It is usually represented as a vector in Euclidean space.
Angle: It is the quantitative measurement of direction.
Direction effect: Similar to distance effect, direction effect depicts the influence of direction in geospatial process and its generated pattern.
(An)Isotropy: Isotropy means uniformity in all directions while anisotropy indicates the existence of variation in different directions.
Similar to distance, direction is used as a way to describe the relations between geographic features. Specifically, it is often applied to indicate the location and movement of geographic features. Before we had technologies such as GPS, our ancestors had learned to navigate on the sea by checking the relation between a boat’s moving direction and its orientation toward the Polaris. The development of geometry further advanced our understanding of direction and, most importantly, provided us a way to quantitatively measure, and thus compare directions. This article discusses the measurement of direction from both a quantitative and qualitative perspective.
2.1 Quantitative Direction
The concept of angles is used to quantitatively measure direction. To do so, one must define an initial direction and an orientation first, which is depicted in Figure 1. A.
In GIS, direction is primarily studied on a Euclidean plane (or space), whereas direction is commonly represented as a vector using the coordinates of two points (e.g., origin and destination). For example, in the Cartesian coordinate system there are two points P1: (x1, y1) and P2: (x2, y2), and their direction is defined as the vector : (Δx, Δy), where Δx = x2 - x1 and Δy = y2 - y1. If one of the orthogonal axes is considered the initial direction (e.g., axis x) and the orientation towards the other axis (e.g., axis y) is defined as the orientation, then the angle of the vector can be computed as: . This is depicted geometrically in Figure 1.B.
In contrast to the Cartesian coordinate system, the polar coordinate system is a more straightforward way to measure direction angle on a Euclidean plane. In fact, the angle is explicitly used to form the two-dimensional coordinate. As Figure 1.C demonstrates, in the polar coordinate system where L is the polar axis and O is the pole, the location of a point is represented as (θ, r) with θ being the angle of the direction and r the distance from the pole to the target point.
Coordinates can be converted between the Cartesian coordinate system and the polar coordinate system. Specific formulas can be found in almost any geometry textbooks. The Cartesian coordinate system is widely used in GIS, so the following discussions will use it as the default coordinate system to discuss properties and operations of directions. It is also worth noting that these coordinate systems can be extended from a plane to a sphere as well. On a sphere, two angles, e.g., latitude and longitude, are often used to locate a point.
In the Cartesian coordinate system, it is also possible to measure the angle even if the initial direction does not align to the axis. Specifically, the angle can be used to measure the relation between two arbitrary directions, which are represented as two vectors in this system. For example, in Figure 1.D there are two vectors : (Δx12, Δy12) and : (Δx34, Δy34) ; the angle θ between these two directions is computed as cos θ = . Differences between the angles in Figures 1.B and 1.D result from the concepts of stationary and radial isotropy (Zhu et al., 2019).
Figure 1. Measures of direction. Source: authors.
Angles are commonly quantified using the unit of degree (º) or radian (rad). The range of degree is from 0º to 360º, and it can be a decimal or in the format of “degree-minute-second” (1º = 60' = 360"). The range of radian is from 0 to 2π . The relation between degree and radian is: 1º = . There is no restriction on which unit should be used in GIS, but in practice, if the angle is used in mathematical computations, the unit of radian is commonly used, whereas if the goal is to navigate or to visualize angles on maps, the unit of degree is frequently applied. Further, although the definition of angle does not support negative values, a negative sign is commonly used to indicate that the orientation is in the opposite direction. For example, if a direction is measured as −θ in the reference system of Figure 1.A, it means that the direction is θ away from the initial direction in a counter-clockwise orientation. Alternatively, the same angle can be measured as 360 − θ (in degree) or 2π − θ (in radian).
2.2 Qualitative Direction
Contrary to quantitative relation that relies on geometric computations, qualitative direction is based on comparisons without using any numeric values. This section explains two types of classic qualitative direction: cardinal and projective, as well as their vagueness in natural language.
2.2.1 Cardinal Directions
Cardinal directions are categorized into north, south, east, and west (and in a finer granularity, four more directions can be added: northeast, northwest, southeast, and southwest). These are frequently used in navigation and astronomy. Using cardinal directions, the initial direction is defined as the north-south line, which establishes the reference of the “north.” There are multiple widely used “north” references. True north (or geographical north) uses the North Pole as the reference and is along the direction of longitude lines. To determine where the North Pole is, people in ancient times used stars such as Polaris, while more recently the gyrocompass was designed, which would not be influenced by the time of the day or weather conditions. The second commonly applied “north” is measured by a magnetic compass, and is appropriately called magnetic north. In this reference, “north” aligns to earth’s magnetic lines of force rather than the axis of the earth’s rotation. Lastly, for projected maps (e.g., Universal Transverse Mercator), “north” is sometimes referred to as the grid north, which is defined locally for zones or grids and it is aligned with the central meridian. It is worth noting that directions of the north-south lines in these different reference systems do not align with each other in most cases. To visualize cardinal direction, the compass rose is often used.
Cardinal direction can be quantified using the concept of azimuth and bearing. In terms of azimuth, the initial direction can be any of the aforementioned “north” and the orientation is clockwise. The angle of azimuth ranges from 0º (north), through 90º (east), 180º (south) and 270º (west), to 360º (north again and coincides with 0º). The bearing also uses one of the aforementioned north-south line as the reference, but the orientation can be either clockwise or counter-clockwise starting from either the “north” or the “south.” Therefore, the angle for bearing ranges from 0º to 90º. A typical format of bearing is like: North 25º West, meaning the target direction is 25º away from the original direction “north,” and the orientation is toward the west, i.e., counter-clockwise (Figure 2).
Figure 2. Example of bearing. Source: authors.
So far, directions are all discussed in Euclidean space. However, when space is curved (non-Euclidean space), direction over long distances should be operated differently. For instance, the direction for a great circle on the surface of the earth is called true azimuth, with its angle constantly changing across successive meridians; however, in cases when the great circle coincides with the equator or any meridian, it is named constant azimuth (Campbell, 1993).
2.2.2 Projective Directions
In contrast to cardinal directions, which use a global reference system, projective directions adopt a local view. Examples of (ternary) projective directions include between, before, left of, and so forth; these are frequently used in our daily lives and they apply an intrinsic or deictic frame of reference (cardinal directions use an extrinsic frame of reference). Clementini (2013) defined a 5-intersection model to classify ternary projective directions among three geographic features without specifically referring to any frame of reference (see Figure 3). To infer ternary projective relations based on observed ones, Clementini et al. (2019) proposed a reasoning system that applied both permutation and composition rules.
Figure 3. Five-intersection model for ternary projective relations between points. Source: authors.
2.2.3 Vagueness in Qualitative Directions
Many of these aforementioned qualitative directions correspond to some English prepositions, which are frequently used in our daily wayfinding, robotics, and geospatial question answering (Retz-Schmidt, 1988). For example, we use verbal route direction, like turn slightly left at the next crossing, to assist navigation. However, the usage of such qualitative directions in natural language can be ambiguous. For example, when using projective directions, the frame of reference is often ambiguous so a cognitive agent must rely on contexts to interpret them (Bateman, 2010). Specifically focusing on route direction, Richer and Klippel (2007), for instance, developed a computational approach to disambiguate quantitative directional relations between decision point and landmark. This type of computational framework further facilitates the disambiguation, representation, and reasoning over qualitative spatial relations in GIS.
Direction has been applied in a variety of spatial studies and applications. The most typical one is to use direction, particularly qualitative direction, for spatial reasoning (Freksa, 1991, Frank, 1996, Clementini, 2009). Since qualitative spatial reasoning can be a single topic in itself and it is often not implemented as a type of GIS operations, this article does not discuss about it in details. Instead, quantitative operations that leverage direction to understand spatial patterns will be discussed.
3.1 Direction in Spatial Interactions
Spatial interaction is commonly defined as flows between geographic entities, where the flow is often represented as a vector embedding both the distance and direction information (Haynes and Fotheringham, 1984). Since direction is explicitly included in the definition of flows, many operations from this group have taken direction into account. Below are some examples.
3.1.1 Basic Raster Operations
To compute direction for each cell in a raster, the operation of flow direction is commonly used in GIS. This operation computes the direction of cells as the steepest descent of the target attribute in the neighborhood. One example is the computation of aspect in digital elevation model (DEM). Similarly, flow accumulation computes the (weighted) accumulation of flows to the downslope target cell. These flow-based operations are intensively used in hydrological applications (e.g., to determine stream flow). Another basic operation is the Euclidean direction, which identifies the direction to the nearest source for each cell. There are also basic statistical operations to describe the pattern of directions. For example, directional mean statistically represents the general directional trend of flows and angular variance indicates the statistical deviation of flows from directional mean. More advanced statistics about directions of the flow can be found in Mardia and Jupp (2009).
3.1.2 Vector Fields (or Flow Fields)
Vector field visualizes raster data using vector symbols, which captures both the magnitude and direction of the flow. One example is the flow field of the wind, which is depicted in Figure 4. As can be seen, each raster cell is represented as a symbol with the length representing the magnitude of the wind and the arrow indicating its direction. Thanks to the continuity nature of the vector field, techniques have been developed for interpolating vector field, which is similar to the interpolation over general fields but with direction being included. Readers are encouraged to refer to Tobler's work (1975) for details.
Figure 4. Example of a Vector field. Source: Esri.
3.1.3 Vector-based Moran's I
To quantitatively measure spatial autocorrelation of vectors (flows), vector-based Moran’s I is designed, which is a generalization of traditional Moran’s I with direction being added in the formula. Specifically, this operation replaces the original scalar observation in Moran's I with the vector one, which is formulated as:
,
where and , and the vector is defined with the origin () and destination ().
Spatial weight matrix w is determined by considering either the origin neighborhood or destination neighborhood, or even both. Detailed discussions can be found in Liu et al., (2015). In addition to Moran’s I, other spatial autocorrelation measures (i.e., Geary’s C), can also be generalized to a vector version by including direction.
3.1.4 Clustering of Flows
Like spatial point clustering, cluster detection of spatial flows is regarded as an essential technique to understand the pattern of flows. In contrast to spatial point clustering (where only distance is used to model spatial proximity), spatial flow clustering takes the direction of flows into account. There are multiple approaches to cluster flows, with direction being either explicitly (Zhu et al., 2019, Yao et al., 2018) or implicitly included (Tao and Thill, 2016). As long as spatial proximity is measured with the inclusion of direction, a traditional clustering technique (such as Ripley’s K and hot spot analysis) can be adopted.
3.2 Direction in Spatial Structures
In addition to spatial flows, directional information can also be used to help understand the spatial structure of point patterns and geostatistical data. In these cases, directional information is not explicitly embedded in the representation of geographic features (e.g., point or cell) like the vector-based flow, but is computed on the fly to analyze relations between geographic features. As in the case of distance effect, this kind of information is named direction effect.
3.2.1 Direction Effect in Spatial Point Patterns
To quantify directional pattern of spatial points, a standard deviation ellipse can be first applied, in which the orientation of the major axis aligns with the directional trend of the point pattern (see Figure 5). Next, an angle-dependent K function (Ohser and Stoyan, 1981) can be used to detect if any direction-dependent point cluster exists. Finally, anisotropic density-based clustering algorithm (Mai et al., 2018) is optional for clustering these points into groups with the direction of point densities being considered. More advanced directional operations to study the anisotropy of spatial point patterns can be found in Rajala et al., (2018).
Figure 5. Example of Standard Deviation Ellipse for a Spatial Point Pattern. Source: authors.
3.2.2 Direction Effect in Geostatistical Data
Widely applied geostatistical models, such as Kriging, have their anisotropic versions as well, in which spatial dependency and isotropy are jointly modeled through a directional semivariogram. This is a generalization of the traditional semivariogram method but is established along different directions (e.g., north–south, west–east, and so forth). Figure 6 shows an example of using directional semivariogram to investigate the spatial pattern of zinc concentrations in a region. It is observed that in different directions, empirical semivariograms vary, which uncovers the fact that this spatial pattern is anisotropic.
Figure 6. Example of a Directional Semivariogram. Source: Zhu et al. 2019.
The next step in Kriging is to fit these empirical directional semivariograms as a continuous covariance function. Depending on whether it is geometric anisotropy (where ranges of directional semivariogram differ) or zonal anisotropy (where both ranges and sills are different for various directions), multiple anisotropic models can be applied. The key idea underlying these operations is to convert the originally anisotropic geographic field into an isotropic one through a series of transformations, such as rotation and translation. As such, traditional isotropic semivariogram models can be used to fit anisotropic data. For details, readers are encouraged to review Chapter 4 of Goovaerts (1997).
3.3 Other Directional Operations
In addition to the aforementioned directional operations, many other typical GIS operations have their directional versions as well. For instance, the popular buffering operation has an anisotropic version, named shape-based buffering (Mu, 2008), in which the speed of the buffering process in different directions varies depending on the shape of the Voronoi polygons built from a geometry set. Another example is the network weight matrix developed for spatial network analysis (Ermagun and Levinson, 2018). Different from the spatial weight matrix, a network weight matrix encodes topological information, such as edge direction, into the spatial network analysis. Further, to explore the effect of direction, Zhu et al. (2019) proposed an angular variogram, as an analogy to distance-based semivariogram, where relations between geographic features are modeled solely based on the basis of angles rather than distances. However, it is worth noting that despite the success of these methods in academia, they currently are rarely found among GIS vendors.
Both as the most fundamental concept in GIS, distance and direction are closely related. Distance is a scalar quantify that measures how far two locations are while angles measure the direction between the two locations. Describing spatial relation between two objects in either Euclidean or spherical space (e.g., locating an object in reference to the origin) requires both distance and direction, which leads to a vector quantity. For example, if we know the coordinate of Point A and there is another Point B that is 500 meters away from it, the location of Point B is undetermined. Only when the direction between Point A and B is also provided (e.g., B is north of A), we can determine the location of B in reference to A. Likewise, if we only know that B is north of A, its location cannot be fixed either.
Despite their close relatedness, distance and direction play different roles in GIS. For example, distance is often used to describe the static relations between two objects while direction indicates the dynamic trend. Two opposing scenarios can explain it: two objects can be close in distance but based on direction they are moving away from each other; two objects that are far away from each other might be moving toward each other. More fundamentally, distance measures spatial relation between two points while direction depicts the relation between two vectors, each of which is composed of at least two points. This is clearly exemplified by the aforementioned definition of angle, which is the relation between the target direction and an initial direction (these two directions are represented as vectors in Euclidean space). Therefore, distance operations are examples of pairwise spatial interactions while directional operations model higher-order interactions that involve more than two geographic features (Zhu et al., 2017).
References:
Aksoy, S., & Cinbis, R. G. (2009). Image mining using directional spatial constraints. IEEE Geoscience and Remote Sensing Letters, 7(1), 33-37. DOI: 10.1109/LGRS.2009.2014083
Bateman, J. A. (2010). Language and space: a two-level semantic approach based on principles of ontological engineering. International Journal of Speech Technology, 13(1), 29-48. DOI: 10.1007/s10772-010-9069-x
Bateman, J. A., Hois, J., Ross, R., & Tenbrink, T. (2010). A linguistic ontology of space for natural language processing. Artificial Intelligence, 174(14), 1027-1071. DOI: 10.1016/j.artint.2010.05.008
Campbell, J. (1993). Map use and analysis. Dubuque: Wm. C. Brown.
Clementini, E. (2013). Directional relations and frames of reference. GeoInformatica, 17(2), 235-255. DOI: 10.1007/s10707-011-0147-2
Clementini, E., Skiadopoulos, S., Billen, R., & Tarquini, F. (2009). A reasoning system of ternary projective relations. IEEE Transactions on Knowledge and Data Engineering, 22(2), 161-178. DOI: 10.1109/TKDE.2009.79
Ermagun, A., & Levinson, D. (2018). An introduction to the network weight matrix. Geographical Analysis, 50(1), 76-96. DOI: 10.1111/gean.12134
Frank, A. U. (1996). Qualitative spatial reasoning: Cardinal directions as an example. International Journal of Geographical Information Science, 10(3), 269-290. DOI: 10.1080/02693799608902079
Freksa, C. (1991). Qualitative spatial reasoning. In Cognitive and linguistic aspects of geographic space (pp. 361-372). Springer, Dordrecht. DOI: 10.1007/978-94-011-2606-9_20
Goovaerts, P. (1997). Geostatistics for natural resources evaluation. Oxford University Press on Demand.
Haynes, K. E., & Fotheringham, A. S. (1984). Gravity and spatial interaction models (Vol. 2). Beverly Hills, CA: Sage.
Liu, Y., Tong, D., & Liu, X. (2015). Measuring spatial autocorrelation of vectors. Geographical Analysis, 47(3), 300-319. DOI: 0.1111/gean.12069
Mai, G., Janowicz, K., Hu, Y., & Gao, S. (2018). ADCN: An anisotropic density‐based clustering algorithm for discovering spatial point patterns with noise. Transactions in GIS, 22(1), 348-369. DOI: 10.1111/tgis.12313
Mardia, K. V., & Jupp, P. E. (2009). Directional statistics (Vol. 494). John Wiley & Sons.
Mu, L. (2008). A shape-based buffering method. Environment and Planning B: Planning and Design, 35(3), 399-412. DOI: doi.org/10.1068/b33046
Ohser, J., & Stoyan, D. (1981). On the second‐order and orientation analysis of planar stationary point processes. Biometrical Journal, 23(6), 523-533. DOI: 10.1002/bimj.4710230602
Rajala, T., Redenbach, C., Särkkä, A., & Sormani, M. (2018). A review on anisotropy analysis of spatial point patterns. Spatial Statistics, 28, 141-168. DOI: 10.1016/j.spasta.2018.04.005
Retz-Schmidt, G. (1988). Various views on spatial prepositions. AI magazine, 9(2), 95-95. DOI: doi.org/10.1609/aimag.v9i2.678
Richter, K. F., & Klippel, A. (2006, September). Before or after: Prepositions in spatially constrained systems. In International Conference on Spatial Cognition (pp. 453-469). Springer, Berlin, Heidelberg. DOI: 10.1007/978-3-540-75666-8_26
Tao, R., & Thill, J. C. (2016). Spatial cluster detection in spatial flow data. Geographical Analysis, 48(4), 355-372. DOI: 10.1111/gean.12100
Tobler, W. R. (1970). A computer movie simulating urban growth in the Detroit region. Economic geography, 46(sup1), 234-240.
Tobler, W. (1975). Spatial interaction patterns. Journal of Environmental Systems 6, 271–301.
Worboys, M. F., & Duckham, M. (2004). GIS: a computing perspective. CRC press.
Yao, X., Zhu, D., Gao, Y., Wu, L., Zhang, P., & Liu, Y. (2018). A stepwise spatiotemporal flow clustering method for discovering mobility trends. IEEE Access, 6, 44666-44675. DOI: 0.1109/ACCESS.2018.2864662
Zhu, R., Kyriakidis, P. C., & Janowicz, K. (2017, May). Beyond pairs: generalizing the geo-dipole for quantifying spatial patterns in geographic fields. In The Annual International Conference on Geographic Information Science (pp. 331-348). Springer, Cham. DOI: 10.1007/978-3-319-56759-4_19
Zhu, R., Janowicz, K., & Mai, G. (2019). Making direction a first‐class citizen of Tobler's first law of geography. Transactions in GIS, 23(3), 398-416. DOI:10.1111/tgis.12550
Learning Objectives:
Describe different ways to measure direction quantitatively.
Identify the intrinsic properties of angles and illustrate how to connect them with directional operations.
Name five types of qualitative direction and indicate the frames of reference for each.
Evaluate whether directional operations are needed and in what types.
Instructional Assessment Questions:
List the two necessary components to measure direction and explain their importance in terms of directional operations.
Explain direction effect and give an example.
Distinguish fundamentals between distance and direction in terms of describing spatial relations.
Describe scenarios in which directional operation is required.
In the same manner as distance, direction plays an equally important role in GIS. This article first summarizes different ways of measuring direction, either quantitatively or qualitatively. Formulas and examples are provided. In the following discussion, fundamental differences between distance and direction in describing spatial relations is examined; properties of angles are emphasized in the context of GIS; and the classification of both cardinal and projective direction is illustrated. With a focus on quantitative operations, various directional operations are categorized and elaborated based on factors such as the underlying data model (vector or raster) and whether direction effect is explicitly or implicitly embedded in the data.
Zhu, R. (2021). Directional Operations. The Geographic Information Science & Technology Body of Knowledge (4th Quarter 2021 Edition), John P. Wilson (ed.). DOI: 10.22224/gistbok/2021.4.2.
This entry is also available in an earlier edition:
DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Distance, Length, and Direction. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital).
1. Definitions
Direction: Direction in GIS generally means the position towards which a geographic feature moves or faces. It is usually represented as a vector in Euclidean space.
Angle: It is the quantitative measurement of direction.
Direction effect: Similar to distance effect, direction effect depicts the influence of direction in geospatial process and its generated pattern.
(An)Isotropy: Isotropy means uniformity in all directions while anisotropy indicates the existence of variation in different directions.
2. Measuring Direction in GIS
Similar to distance, direction is used as a way to describe the relations between geographic features. Specifically, it is often applied to indicate the location and movement of geographic features. Before we had technologies such as GPS, our ancestors had learned to navigate on the sea by checking the relation between a boat’s moving direction and its orientation toward the Polaris. The development of geometry further advanced our understanding of direction and, most importantly, provided us a way to quantitatively measure, and thus compare directions. This article discusses the measurement of direction from both a quantitative and qualitative perspective.
2.1 Quantitative Direction
The concept of angles is used to quantitatively measure direction. To do so, one must define an initial direction and an orientation first, which is depicted in Figure 1. A.
In GIS, direction is primarily studied on a Euclidean plane (or space), whereas direction is commonly represented as a vector using the coordinates of two points (e.g., origin and destination). For example, in the Cartesian coordinate system there are two points P1: (x1, y1) and P2: (x2, y2), and their direction is defined as the vector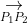 : (Δx, Δy), where Δx = x2 - x1 and Δy = y2 - y1. If one of the orthogonal axes is considered the initial direction (e.g., axis x) and the orientation towards the other axis (e.g., axis y) is defined as the orientation, then the angle of the vector can be computed as:
: (Δx, Δy), where Δx = x2 - x1 and Δy = y2 - y1. If one of the orthogonal axes is considered the initial direction (e.g., axis x) and the orientation towards the other axis (e.g., axis y) is defined as the orientation, then the angle of the vector can be computed as: 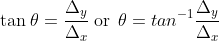 . This is depicted geometrically in Figure 1.B.
. This is depicted geometrically in Figure 1.B.
In contrast to the Cartesian coordinate system, the polar coordinate system is a more straightforward way to measure direction angle on a Euclidean plane. In fact, the angle is explicitly used to form the two-dimensional coordinate. As Figure 1.C demonstrates, in the polar coordinate system where L is the polar axis and O is the pole, the location of a point is represented as (θ, r) with θ being the angle of the direction and r the distance from the pole to the target point.
Coordinates can be converted between the Cartesian coordinate system and the polar coordinate system. Specific formulas can be found in almost any geometry textbooks. The Cartesian coordinate system is widely used in GIS, so the following discussions will use it as the default coordinate system to discuss properties and operations of directions. It is also worth noting that these coordinate systems can be extended from a plane to a sphere as well. On a sphere, two angles, e.g., latitude and longitude, are often used to locate a point.
In the Cartesian coordinate system, it is also possible to measure the angle even if the initial direction does not align to the axis. Specifically, the angle can be used to measure the relation between two arbitrary directions, which are represented as two vectors in this system. For example, in Figure 1.D there are two vectors : (Δx12, Δy12) and
: (Δx12, Δy12) and  : (Δx34, Δy34) ; the angle θ between these two directions is computed as cos θ =
: (Δx34, Δy34) ; the angle θ between these two directions is computed as cos θ = 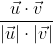 . Differences between the angles in Figures 1.B and 1.D result from the concepts of stationary and radial isotropy (Zhu et al., 2019).
. Differences between the angles in Figures 1.B and 1.D result from the concepts of stationary and radial isotropy (Zhu et al., 2019).
Figure 1. Measures of direction. Source: authors.
Angles are commonly quantified using the unit of degree (º) or radian (rad). The range of degree is from 0º to 360º, and it can be a decimal or in the format of “degree-minute-second” (1º = 60' = 360"). The range of radian is from 0 to 2π . The relation between degree and radian is: 1º =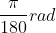 . There is no restriction on which unit should be used in GIS, but in practice, if the angle is used in mathematical computations, the unit of radian is commonly used, whereas if the goal is to navigate or to visualize angles on maps, the unit of degree is frequently applied. Further, although the definition of angle does not support negative values, a negative sign is commonly used to indicate that the orientation is in the opposite direction. For example, if a direction is measured as −θ in the reference system of Figure 1.A, it means that the direction is θ away from the initial direction in a counter-clockwise orientation. Alternatively, the same angle can be measured as 360 − θ (in degree) or 2π − θ (in radian).
. There is no restriction on which unit should be used in GIS, but in practice, if the angle is used in mathematical computations, the unit of radian is commonly used, whereas if the goal is to navigate or to visualize angles on maps, the unit of degree is frequently applied. Further, although the definition of angle does not support negative values, a negative sign is commonly used to indicate that the orientation is in the opposite direction. For example, if a direction is measured as −θ in the reference system of Figure 1.A, it means that the direction is θ away from the initial direction in a counter-clockwise orientation. Alternatively, the same angle can be measured as 360 − θ (in degree) or 2π − θ (in radian).
2.2 Qualitative Direction
Contrary to quantitative relation that relies on geometric computations, qualitative direction is based on comparisons without using any numeric values. This section explains two types of classic qualitative direction: cardinal and projective, as well as their vagueness in natural language.
2.2.1 Cardinal Directions
Cardinal directions are categorized into north, south, east, and west (and in a finer granularity, four more directions can be added: northeast, northwest, southeast, and southwest). These are frequently used in navigation and astronomy. Using cardinal directions, the initial direction is defined as the north-south line, which establishes the reference of the “north.” There are multiple widely used “north” references. True north (or geographical north) uses the North Pole as the reference and is along the direction of longitude lines. To determine where the North Pole is, people in ancient times used stars such as Polaris, while more recently the gyrocompass was designed, which would not be influenced by the time of the day or weather conditions. The second commonly applied “north” is measured by a magnetic compass, and is appropriately called magnetic north. In this reference, “north” aligns to earth’s magnetic lines of force rather than the axis of the earth’s rotation. Lastly, for projected maps (e.g., Universal Transverse Mercator), “north” is sometimes referred to as the grid north, which is defined locally for zones or grids and it is aligned with the central meridian. It is worth noting that directions of the north-south lines in these different reference systems do not align with each other in most cases. To visualize cardinal direction, the compass rose is often used.
Cardinal direction can be quantified using the concept of azimuth and bearing. In terms of azimuth, the initial direction can be any of the aforementioned “north” and the orientation is clockwise. The angle of azimuth ranges from 0º (north), through 90º (east), 180º (south) and 270º (west), to 360º (north again and coincides with 0º). The bearing also uses one of the aforementioned north-south line as the reference, but the orientation can be either clockwise or counter-clockwise starting from either the “north” or the “south.” Therefore, the angle for bearing ranges from 0º to 90º. A typical format of bearing is like: North 25º West, meaning the target direction is 25º away from the original direction “north,” and the orientation is toward the west, i.e., counter-clockwise (Figure 2).
Figure 2. Example of bearing. Source: authors.
So far, directions are all discussed in Euclidean space. However, when space is curved (non-Euclidean space), direction over long distances should be operated differently. For instance, the direction for a great circle on the surface of the earth is called true azimuth, with its angle constantly changing across successive meridians; however, in cases when the great circle coincides with the equator or any meridian, it is named constant azimuth (Campbell, 1993).
2.2.2 Projective Directions
In contrast to cardinal directions, which use a global reference system, projective directions adopt a local view. Examples of (ternary) projective directions include between, before, left of, and so forth; these are frequently used in our daily lives and they apply an intrinsic or deictic frame of reference (cardinal directions use an extrinsic frame of reference). Clementini (2013) defined a 5-intersection model to classify ternary projective directions among three geographic features without specifically referring to any frame of reference (see Figure 3). To infer ternary projective relations based on observed ones, Clementini et al. (2019) proposed a reasoning system that applied both permutation and composition rules.
Figure 3. Five-intersection model for ternary projective relations between points. Source: authors.
2.2.3 Vagueness in Qualitative Directions
Many of these aforementioned qualitative directions correspond to some English prepositions, which are frequently used in our daily wayfinding, robotics, and geospatial question answering (Retz-Schmidt, 1988). For example, we use verbal route direction, like turn slightly left at the next crossing, to assist navigation. However, the usage of such qualitative directions in natural language can be ambiguous. For example, when using projective directions, the frame of reference is often ambiguous so a cognitive agent must rely on contexts to interpret them (Bateman, 2010). Specifically focusing on route direction, Richer and Klippel (2007), for instance, developed a computational approach to disambiguate quantitative directional relations between decision point and landmark. This type of computational framework further facilitates the disambiguation, representation, and reasoning over qualitative spatial relations in GIS.
3. Directional Operations in GIS
Direction has been applied in a variety of spatial studies and applications. The most typical one is to use direction, particularly qualitative direction, for spatial reasoning (Freksa, 1991, Frank, 1996, Clementini, 2009). Since qualitative spatial reasoning can be a single topic in itself and it is often not implemented as a type of GIS operations, this article does not discuss about it in details. Instead, quantitative operations that leverage direction to understand spatial patterns will be discussed.
3.1 Direction in Spatial Interactions
Spatial interaction is commonly defined as flows between geographic entities, where the flow is often represented as a vector embedding both the distance and direction information (Haynes and Fotheringham, 1984). Since direction is explicitly included in the definition of flows, many operations from this group have taken direction into account. Below are some examples.
3.1.1 Basic Raster Operations
To compute direction for each cell in a raster, the operation of flow direction is commonly used in GIS. This operation computes the direction of cells as the steepest descent of the target attribute in the neighborhood. One example is the computation of aspect in digital elevation model (DEM). Similarly, flow accumulation computes the (weighted) accumulation of flows to the downslope target cell. These flow-based operations are intensively used in hydrological applications (e.g., to determine stream flow). Another basic operation is the Euclidean direction, which identifies the direction to the nearest source for each cell. There are also basic statistical operations to describe the pattern of directions. For example, directional mean statistically represents the general directional trend of flows and angular variance indicates the statistical deviation of flows from directional mean. More advanced statistics about directions of the flow can be found in Mardia and Jupp (2009).
3.1.2 Vector Fields (or Flow Fields)
Vector field visualizes raster data using vector symbols, which captures both the magnitude and direction of the flow. One example is the flow field of the wind, which is depicted in Figure 4. As can be seen, each raster cell is represented as a symbol with the length representing the magnitude of the wind and the arrow indicating its direction. Thanks to the continuity nature of the vector field, techniques have been developed for interpolating vector field, which is similar to the interpolation over general fields but with direction being included. Readers are encouraged to refer to Tobler's work (1975) for details.
Figure 4. Example of a Vector field. Source: Esri.
3.1.3 Vector-based Moran's I
To quantitatively measure spatial autocorrelation of vectors (flows), vector-based Moran’s I is designed, which is a generalization of traditional Moran’s I with direction being added in the formula. Specifically, this operation replaces the original scalar observation in Moran's I with the vector one, which is formulated as:
where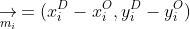 and
and 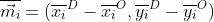 , and the vector is defined with the origin (
, and the vector is defined with the origin (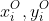 ) and destination (
) and destination (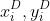 ).
).
Spatial weight matrix w is determined by considering either the origin neighborhood or destination neighborhood, or even both. Detailed discussions can be found in Liu et al., (2015). In addition to Moran’s I, other spatial autocorrelation measures (i.e., Geary’s C), can also be generalized to a vector version by including direction.
3.1.4 Clustering of Flows
Like spatial point clustering, cluster detection of spatial flows is regarded as an essential technique to understand the pattern of flows. In contrast to spatial point clustering (where only distance is used to model spatial proximity), spatial flow clustering takes the direction of flows into account. There are multiple approaches to cluster flows, with direction being either explicitly (Zhu et al., 2019, Yao et al., 2018) or implicitly included (Tao and Thill, 2016). As long as spatial proximity is measured with the inclusion of direction, a traditional clustering technique (such as Ripley’s K and hot spot analysis) can be adopted.
3.2 Direction in Spatial Structures
In addition to spatial flows, directional information can also be used to help understand the spatial structure of point patterns and geostatistical data. In these cases, directional information is not explicitly embedded in the representation of geographic features (e.g., point or cell) like the vector-based flow, but is computed on the fly to analyze relations between geographic features. As in the case of distance effect, this kind of information is named direction effect.
3.2.1 Direction Effect in Spatial Point Patterns
To quantify directional pattern of spatial points, a standard deviation ellipse can be first applied, in which the orientation of the major axis aligns with the directional trend of the point pattern (see Figure 5). Next, an angle-dependent K function (Ohser and Stoyan, 1981) can be used to detect if any direction-dependent point cluster exists. Finally, anisotropic density-based clustering algorithm (Mai et al., 2018) is optional for clustering these points into groups with the direction of point densities being considered. More advanced directional operations to study the anisotropy of spatial point patterns can be found in Rajala et al., (2018).
Figure 5. Example of Standard Deviation Ellipse for a Spatial Point Pattern. Source: authors.
3.2.2 Direction Effect in Geostatistical Data
Widely applied geostatistical models, such as Kriging, have their anisotropic versions as well, in which spatial dependency and isotropy are jointly modeled through a directional semivariogram. This is a generalization of the traditional semivariogram method but is established along different directions (e.g., north–south, west–east, and so forth). Figure 6 shows an example of using directional semivariogram to investigate the spatial pattern of zinc concentrations in a region. It is observed that in different directions, empirical semivariograms vary, which uncovers the fact that this spatial pattern is anisotropic.
Figure 6. Example of a Directional Semivariogram. Source: Zhu et al. 2019.
The next step in Kriging is to fit these empirical directional semivariograms as a continuous covariance function. Depending on whether it is geometric anisotropy (where ranges of directional semivariogram differ) or zonal anisotropy (where both ranges and sills are different for various directions), multiple anisotropic models can be applied. The key idea underlying these operations is to convert the originally anisotropic geographic field into an isotropic one through a series of transformations, such as rotation and translation. As such, traditional isotropic semivariogram models can be used to fit anisotropic data. For details, readers are encouraged to review Chapter 4 of Goovaerts (1997).
3.3 Other Directional Operations
In addition to the aforementioned directional operations, many other typical GIS operations have their directional versions as well. For instance, the popular buffering operation has an anisotropic version, named shape-based buffering (Mu, 2008), in which the speed of the buffering process in different directions varies depending on the shape of the Voronoi polygons built from a geometry set. Another example is the network weight matrix developed for spatial network analysis (Ermagun and Levinson, 2018). Different from the spatial weight matrix, a network weight matrix encodes topological information, such as edge direction, into the spatial network analysis. Further, to explore the effect of direction, Zhu et al. (2019) proposed an angular variogram, as an analogy to distance-based semivariogram, where relations between geographic features are modeled solely based on the basis of angles rather than distances. However, it is worth noting that despite the success of these methods in academia, they currently are rarely found among GIS vendors.
4. Distance vs. Direction
Both as the most fundamental concept in GIS, distance and direction are closely related. Distance is a scalar quantify that measures how far two locations are while angles measure the direction between the two locations. Describing spatial relation between two objects in either Euclidean or spherical space (e.g., locating an object in reference to the origin) requires both distance and direction, which leads to a vector quantity. For example, if we know the coordinate of Point A and there is another Point B that is 500 meters away from it, the location of Point B is undetermined. Only when the direction between Point A and B is also provided (e.g., B is north of A), we can determine the location of B in reference to A. Likewise, if we only know that B is north of A, its location cannot be fixed either.
Despite their close relatedness, distance and direction play different roles in GIS. For example, distance is often used to describe the static relations between two objects while direction indicates the dynamic trend. Two opposing scenarios can explain it: two objects can be close in distance but based on direction they are moving away from each other; two objects that are far away from each other might be moving toward each other. More fundamentally, distance measures spatial relation between two points while direction depicts the relation between two vectors, each of which is composed of at least two points. This is clearly exemplified by the aforementioned definition of angle, which is the relation between the target direction and an initial direction (these two directions are represented as vectors in Euclidean space). Therefore, distance operations are examples of pairwise spatial interactions while directional operations model higher-order interactions that involve more than two geographic features (Zhu et al., 2017).
Aksoy, S., & Cinbis, R. G. (2009). Image mining using directional spatial constraints. IEEE Geoscience and Remote Sensing Letters, 7(1), 33-37. DOI: 10.1109/LGRS.2009.2014083
Bateman, J. A. (2010). Language and space: a two-level semantic approach based on principles of ontological engineering. International Journal of Speech Technology, 13(1), 29-48. DOI: 10.1007/s10772-010-9069-x
Bateman, J. A., Hois, J., Ross, R., & Tenbrink, T. (2010). A linguistic ontology of space for natural language processing. Artificial Intelligence, 174(14), 1027-1071. DOI: 10.1016/j.artint.2010.05.008
Campbell, J. (1993). Map use and analysis. Dubuque: Wm. C. Brown.
Clementini, E. (2013). Directional relations and frames of reference. GeoInformatica, 17(2), 235-255. DOI: 10.1007/s10707-011-0147-2
Clementini, E., Skiadopoulos, S., Billen, R., & Tarquini, F. (2009). A reasoning system of ternary projective relations. IEEE Transactions on Knowledge and Data Engineering, 22(2), 161-178. DOI: 10.1109/TKDE.2009.79
Ermagun, A., & Levinson, D. (2018). An introduction to the network weight matrix. Geographical Analysis, 50(1), 76-96. DOI: 10.1111/gean.12134
Frank, A. U. (1996). Qualitative spatial reasoning: Cardinal directions as an example. International Journal of Geographical Information Science, 10(3), 269-290. DOI: 10.1080/02693799608902079
Freksa, C. (1991). Qualitative spatial reasoning. In Cognitive and linguistic aspects of geographic space (pp. 361-372). Springer, Dordrecht. DOI: 10.1007/978-94-011-2606-9_20
Goovaerts, P. (1997). Geostatistics for natural resources evaluation. Oxford University Press on Demand.
Haynes, K. E., & Fotheringham, A. S. (1984). Gravity and spatial interaction models (Vol. 2). Beverly Hills, CA: Sage.
Liu, Y., Tong, D., & Liu, X. (2015). Measuring spatial autocorrelation of vectors. Geographical Analysis, 47(3), 300-319. DOI: 0.1111/gean.12069
Mai, G., Janowicz, K., Hu, Y., & Gao, S. (2018). ADCN: An anisotropic density‐based clustering algorithm for discovering spatial point patterns with noise. Transactions in GIS, 22(1), 348-369. DOI: 10.1111/tgis.12313
Mardia, K. V., & Jupp, P. E. (2009). Directional statistics (Vol. 494). John Wiley & Sons.
Mu, L. (2008). A shape-based buffering method. Environment and Planning B: Planning and Design, 35(3), 399-412. DOI: doi.org/10.1068/b33046
Ohser, J., & Stoyan, D. (1981). On the second‐order and orientation analysis of planar stationary point processes. Biometrical Journal, 23(6), 523-533. DOI: 10.1002/bimj.4710230602
Rajala, T., Redenbach, C., Särkkä, A., & Sormani, M. (2018). A review on anisotropy analysis of spatial point patterns. Spatial Statistics, 28, 141-168. DOI: 10.1016/j.spasta.2018.04.005
Retz-Schmidt, G. (1988). Various views on spatial prepositions. AI magazine, 9(2), 95-95. DOI: doi.org/10.1609/aimag.v9i2.678
Richter, K. F., & Klippel, A. (2006, September). Before or after: Prepositions in spatially constrained systems. In International Conference on Spatial Cognition (pp. 453-469). Springer, Berlin, Heidelberg. DOI: 10.1007/978-3-540-75666-8_26
Tao, R., & Thill, J. C. (2016). Spatial cluster detection in spatial flow data. Geographical Analysis, 48(4), 355-372. DOI: 10.1111/gean.12100
Tobler, W. R. (1970). A computer movie simulating urban growth in the Detroit region. Economic geography, 46(sup1), 234-240.
Tobler, W. (1975). Spatial interaction patterns. Journal of Environmental Systems 6, 271–301.
Worboys, M. F., & Duckham, M. (2004). GIS: a computing perspective. CRC press.
Yao, X., Zhu, D., Gao, Y., Wu, L., Zhang, P., & Liu, Y. (2018). A stepwise spatiotemporal flow clustering method for discovering mobility trends. IEEE Access, 6, 44666-44675. DOI: 0.1109/ACCESS.2018.2864662
Zhu, R., Kyriakidis, P. C., & Janowicz, K. (2017, May). Beyond pairs: generalizing the geo-dipole for quantifying spatial patterns in geographic fields. In The Annual International Conference on Geographic Information Science (pp. 331-348). Springer, Cham. DOI: 10.1007/978-3-319-56759-4_19
Zhu, R., Janowicz, K., & Mai, G. (2019). Making direction a first‐class citizen of Tobler's first law of geography. Transactions in GIS, 23(3), 398-416. DOI:10.1111/tgis.12550
Keywords: