Spatial data conflation is the process of combining overlapping spatial datasets to produce a better dataset with higher accuracy or more information. Conflation is needed in many fields, ranging from transportation planning to the analysis of historical datasets, which require the use of multiple data sources. Geospatial data conflation becomes increasingly important with the advancement of GIS and the emergence of new sources of spatial data such as Volunteered Geographic Information.
Conceptually, conflation is a two-step process involving identifying counterpart features that correspond to the same object in reality, and merging the geometry and attributes of counterpart features. In practice, conflation can be performed either manually or with the aid of GIS with varying degrees of automation. Manual conflation is labor-intensive, time consuming and expensive. It is often adopted in practice, nonetheless, due to the lack of reliable automatic conflation methods.
A main challenge of automatic conflation lies in the automatic matching of corresponding features, due to the varying quality and different representations of map data. Many (semi-)automatic feature methods exist. They typically involve measuring the distance between each feature pair and trying to match feature pairs with smaller dissimilarity using a specially designed algorithm or model. Fully automated conflation is still an active research field.
Author and Citation Info:
Lei, T. L. (2019). Geospatial Data Conflation. The Geographic Information Science & Technology Body of Knowledge (3rd Quarter 2019 Edition), John P. Wilson (ed.). DOI: 10.22224/gistbok/2019.3.5
An important operation in spatial analysis is to effectively combine data from different sources. Conflation is the process of combining “two digital map files to produce a third map file which is better than each of the component source maps” (Ruiz et al., 2011). The datasets in conflation typically share certain common features representing the same objects in reality, which need to be matched and merged.
Conflation is important in spatial analyses because different agencies and vendors, each with a different role and scope, often produce spatial data for the same type of objects. A typical conflation problem is the conflation of transportation networks. Due to the importance of roads as corridors of movement and a common reference system, many agencies and organizations provide transportation network data. Public agencies (such as US Census and USGS) maintain well-known road databases such as the TIGER/Line. Private vendors (such as TeleAtlas and Navteq) produce high quality network datasets for navigation purposes. Advancement of sensor technology and the open data movement have made more and more street network data (among other types of data) available to the public as Volunteered Geographic Information (VGI) (Goodchild, 2007). A transportation planner often needs to combine all sorts of information about transportation infrastructure and social-economic characteristics of the population from these data sources in their analyses.
Just like digitization and other data preparation processes, conflation can be a labor-intensive procedure. Due to the volume and the complexity of features in the datasets, conflation can be expensive and time consuming. By comparison, automated conflation methods try to match corresponding features and merge them automatically. Systematic conflation methods range from simple ones using standard GIS operations such as buffer and overlay analysis to more complex ones that measure the similarity between pairs of features and match features in light of spatial context and relations. However, fully automated feature matching and conflation is still difficult at present. For example, basic GIS operations such as buffer and overlay analysis do not work well with the presence of spatial displacement of features common in heterogeneous data. Figure 1 (Lei & Lei, 2019) demonstrates an example of spatial displacement using different road datasets covering Santa Barbara, CA (from Open Street Map, TIGER/Line and TeleAtlas, respectively).
Figure 1. Spatial displacement between different road datasets (Santa Barbara, CA).
Other than manual conflation, computerized conflation methods typically use certain relations between candidate features from two datasets to find potential matches. An important characterization of the match relation between features is the “cardinality” of relations between entities from relational database theory. The cardinality of relation is the number of times of entities from one dataset can be linked to the entities in the other dataset. There are three cases of cardinality of relations. The first (and the simplest) case is the one-to-one matching relation in Figure 2a. This cardinality represents cases in which two corresponding features correspond to the same object in reality.
Figure 2. Cardinality of match for dataset 1 (green) and dataset 2 (red).
The second case is the one-to-many (1:m) matching relation. This case indicates the fact that a group of features in one dataset, when combined, represents the same object as one feature in the other dataset. This can happen, e.g., when a set of shorter road segments corresponds to a road that is represented as a single line in the other dataset (Figure 2b) or when a road is represented as one line in one dataset but two parallel lines (for the two directions of the road) in the other. The third case of cardinality is the many-to-many matching. This includes two-way one-to-many relations in which one-to-many correspondence exists both from dataset 1 to dataset 2 and, in the opposite direction, from dataset 2 to dataset 1. In addition, the many-to-many case also includes more complicated matchings (Figure 2d) in which no feature individually corresponds to a group of features in the other dataset. Features from the two datasets can only represent the same object in reality after grouping individual features in each dataset, respectively. Some conflation algorithms can handle only the simplest one-to-one conflation problems, while others can handle the more complex one-to-many and many-to-many problems.
Depending on the geometric type of datasets, different methods have been developed for matching point features (e.g. gazettes and points of interests [7]), lines (e.g. transportation networks [8]) and polygons (e.g. building footprints, parcels, census tracts [6]), respectively.
To determine the relations between features, conflation methods typically compute certain metrics of similarity or dissimilarity (distance) between potentially related features. The metrics can be based on the geometry, the attributes (e.g. [7]), and topological relationships of the features involved. Similarity in geometry is a widely used metric, which compares the lengths, shapes and orientations of two features. A general method for computing the geometric difference between two features is the Hausdorff distance. Figure 3 demonstrates the computation of Hausdorff distance. For features A and B, the directed Hausdorff distance from A to B is defined as:
where is the distance from a point pA to the point set B. The directed Hausdorff distance equals the maximum deviation of the points of feature A from feature B. Note that, in practice, the approximate Hausdorff distance is often computed using only the vertices of feature A (instead of all points of A) to save computational time (Figure 3b). In Figure 3, the directed Hausdorff distances from A to B (Figure 3b), and from B to A (Figure 3c) are 40 and 57, respectively. The Hausdorff distance between A and B is 57, the larger of the two directed Hausdorff distances. If A coincides with B or a part of B, obviously . The Hausdorff distance is defined to be the maximum of and . It is zero only when features A and B equal each other in geometry. Other distance metrics for measuring geometric differences exist.
Figure 3. Directed Hausdorff distances between a pair of features from two datasets.
Attribute-based metrics compare two features on common attributes such as street names. This can be accomplished, e.g., using string distances such as the Hamming distance or the Levenshtein distance. Topological metrics compare two features based on properties such as the number of edges that enter a node.
The conflation process typically consists of two main steps: 1) feature matching, and 2) feature merging. In addition, some conflation procedures require a preprocessing step e.g., to adjust the location of features and a post-processing step, e.g. to verify and rectify computer generated match results (and re-run conflation if necessary).
4.1. Feature matching
Given a metric of distance (or dissimilarity) between features (Section 3), a simple strategy of conflation is to match features that are the closest. The k-Closest Pairs Queries (KCPQ) seeks to find k pairs of features whose distances are the smallest [1]. However, such a strategy can be easily disrupted by the spatial displacement of features. In the examples in Figure 1. and the cover image, it can be seen that KCPQ can match some corresponding features correctly, while matching other features incorrectly when these features happen to be close to each other but do not represent the same object in reality.
Another commonly-used conflation method is based on buffer analysis and overlay analysis. For example, the simple buffer method [3] measures the similarity of two features as the percentage of one feature that falls in the buffer of the other. Similar to the distance based KCPQ, the buffer methods require the data to be well aligned before conflation.
The well-known “rubber-sheeting” method was designed in 1980s to deal with unevenly distributed location errors. It was one of the earliest systematic conflation method developed by US Census [9, 11] to conflate USGS data. The method selects a set of counterpart points as “anchors” to link two datasets, in such a way that each triangular region between the anchor points should have similar spatial displacement. The rubber-sheeting method then applies an affine transformation in each region to remove the spatial displacement so that a simpler method such as the buffer method can be applied. The rubber-sheeting method has been extended by researchers and is still in use in many GIS conflation tools nowadays. In general, the method is semi-automatic that can still require significant human intervention in choosing anchor points in the area.
4.2. Feature merging
Once the match relation between features is established properly, the information from corresponding features can be merged following predefined rules. This includes the merging of attribute information and geometry. If the match relation is one-to-one, one can combine attribute information by copying the attributes of one feature to its corresponding feature. If the match relation is one-to-many or many-to-many, an attribute needs to be divided and/or combined and then transferred to the corresponding feature. The rule for the transfer depends on the nature of the attribute. Intensive attributes such as population density may be transferred directly, while extensive attributes such as population count need to be divided before the transfer.
There are also different ways of merging geometries. If one dataset has consistently higher spatial accuracy, one may use its geometries and discard the geometries of the other dataset. If two datasets have similar accuracy, one may compute an “average” geometry between two geometries of a pair of corresponding features. After feature matching and feature merging, one may need to evaluate the accuracy and quality of conflated product by comparing with a small set of conflation results performed by human experts (i.e. ground truth).
Conflation is closely related to database operations such as spatial join. Both involve combining information in input datasets. However, there are differences between the two processes. First of all, spatial join is a “local” operation based on selecting individual pairs of features satisfying a spatial condition. It is often performed in two stages [4]: 1) a filter stage in which potentially related objects are selected based on indices and bounding rectangles, and 2) a refinement stage that verifies candidate pairs using the full join condition. By comparison, conflation can consider a larger and more complex spatial context and can consider neighboring features, e.g. when using topology based criteria. Secondly, conflation can involve transforming and merging the geometries of the input feature, which typically is not performed during a spatial join.
Geospatial data conflation is also related to the concept of data fusion. In a broader sense, the two terms are sometimes used interchangeably, but data fusion is traditionally more commonly seen in Remote Sensing [10].
References:
Ahmadi, E., & Nascimento, M. A. (2016). K-closest pairs queries in road networks. 17th IEEE International Conference on Mobile Data Management (MDM). DOI: 10.1109/MDM.2016.44
Goodchild, M. F. (2007). Citizens as Sensors: The World of Volunteered Geography. GeoJournal, 69(4), 211-221. DOI: 10.1007/s10708-007-9111-y
Goodchild, M. F., & Hunter, G. J. (1997). A simple positional accuracy measure for linear features. International Journal of Geographical information science, 11(3), 299-306. DOI: 10.1080/136588197242419
Jacox, E. H., & Samet, H. (2007). Spatial join techniques. ACM Transactions on Database Systems (TODS), 32(1), 7. DOI: 10.1145/1206049.1206056
Lei, T. L., & Lei, Z. (2019). Optimal spatial data matching for conflation: A network flow based approach. Transactions in GIS. In press.
Masuyama, A. (2006). Methods for detecting apparent differences between spatial tessellations at different time points.International Journal of Geographical Information Science, 20(6), 633-648. DOI: 10.1080/13658810600661300
McKenzie, G., Janowicz, K., & Adams, B. (2014). A weighted multi-attribute method for matching user-generated Points of Interest. Cartography and Geographic Information Science, 41(2), 125-137. DOI: 10.1080/15230406.2014.880327
Pendyala, R. M. (2002). Development of GIS-based conflation tools for data integration and matching.
Rosen, B., & Saalfeld, A. (1985). Match criteria for automatic alignment. Proceedings of 7th International Symposium on Computer-assisted Cartography (Auto-Carto 7).
Ruiz, J. J., Ariza, F. J., Urena, M. A., & Blázquez, E. B. (2011). Digital map conflation: a review of the process and a proposal for classification.International Journal of Geographical Information Science, 25(9), 1439-1466. DOI: 10.1080/13658816.2010.519707
Saalfeld, A. (1988). Conflation automated map compilation.International Journal of Geographical Information System, 2(3), 217-228.
Learning Objectives:
Define the concept of conflation and what kind of context it is used.
Describe the basic types of conflation problems.
Understand the cardinality of match relation.
Understand the different criteria used for conflating geospatial features.
Implement basic conflation operator using buffer analysis and overlay operation.
Explain the difference between manual and automatic conflation.
Compare conflation with spatial join, image fusion and other related operations for data integration.
Instructional Assessment Questions:
What is conflation? Give an example of GIS application that would require conflation.
What are the advantages and disadvantages of automated conflation compared with manual conflation?
Obtain two road network datasets from different sources, and try to write a SQL statement to join corresponding streets using street names.
Write a SQL statement (or a GUI interface of a GIS package) to match corresponding road features based on buffer and overlay analysis.
List the different criteria that can be used to match corresponding features.
What are corresponding features? What is the cardinality of match relation?
What are the differences between conflation and spatial join?
Additional Resources:
Obe, R. O., & Hsu, L. S. (2015). PostGIS in action (2nd ed.). Manning Publications Co.
Spatial data conflation is the process of combining overlapping spatial datasets to produce a better dataset with higher accuracy or more information. Conflation is needed in many fields, ranging from transportation planning to the analysis of historical datasets, which require the use of multiple data sources. Geospatial data conflation becomes increasingly important with the advancement of GIS and the emergence of new sources of spatial data such as Volunteered Geographic Information.
Conceptually, conflation is a two-step process involving identifying counterpart features that correspond to the same object in reality, and merging the geometry and attributes of counterpart features. In practice, conflation can be performed either manually or with the aid of GIS with varying degrees of automation. Manual conflation is labor-intensive, time consuming and expensive. It is often adopted in practice, nonetheless, due to the lack of reliable automatic conflation methods.
A main challenge of automatic conflation lies in the automatic matching of corresponding features, due to the varying quality and different representations of map data. Many (semi-)automatic feature methods exist. They typically involve measuring the distance between each feature pair and trying to match feature pairs with smaller dissimilarity using a specially designed algorithm or model. Fully automated conflation is still an active research field.
Lei, T. L. (2019). Geospatial Data Conflation. The Geographic Information Science & Technology Body of Knowledge (3rd Quarter 2019 Edition), John P. Wilson (ed.). DOI: 10.22224/gistbok/2019.3.5
1. Overview
An important operation in spatial analysis is to effectively combine data from different sources. Conflation is the process of combining “two digital map files to produce a third map file which is better than each of the component source maps” (Ruiz et al., 2011). The datasets in conflation typically share certain common features representing the same objects in reality, which need to be matched and merged.
Conflation is important in spatial analyses because different agencies and vendors, each with a different role and scope, often produce spatial data for the same type of objects. A typical conflation problem is the conflation of transportation networks. Due to the importance of roads as corridors of movement and a common reference system, many agencies and organizations provide transportation network data. Public agencies (such as US Census and USGS) maintain well-known road databases such as the TIGER/Line. Private vendors (such as TeleAtlas and Navteq) produce high quality network datasets for navigation purposes. Advancement of sensor technology and the open data movement have made more and more street network data (among other types of data) available to the public as Volunteered Geographic Information (VGI) (Goodchild, 2007). A transportation planner often needs to combine all sorts of information about transportation infrastructure and social-economic characteristics of the population from these data sources in their analyses.
Just like digitization and other data preparation processes, conflation can be a labor-intensive procedure. Due to the volume and the complexity of features in the datasets, conflation can be expensive and time consuming. By comparison, automated conflation methods try to match corresponding features and merge them automatically. Systematic conflation methods range from simple ones using standard GIS operations such as buffer and overlay analysis to more complex ones that measure the similarity between pairs of features and match features in light of spatial context and relations. However, fully automated feature matching and conflation is still difficult at present. For example, basic GIS operations such as buffer and overlay analysis do not work well with the presence of spatial displacement of features common in heterogeneous data. Figure 1 (Lei & Lei, 2019) demonstrates an example of spatial displacement using different road datasets covering Santa Barbara, CA (from Open Street Map, TIGER/Line and TeleAtlas, respectively).
Figure 1. Spatial displacement between different road datasets (Santa Barbara, CA).
2. Types of Conflation Problems
Other than manual conflation, computerized conflation methods typically use certain relations between candidate features from two datasets to find potential matches. An important characterization of the match relation between features is the “cardinality” of relations between entities from relational database theory. The cardinality of relation is the number of times of entities from one dataset can be linked to the entities in the other dataset. There are three cases of cardinality of relations. The first (and the simplest) case is the one-to-one matching relation in Figure 2a. This cardinality represents cases in which two corresponding features correspond to the same object in reality.
Figure 2. Cardinality of match for dataset 1 (green) and dataset 2 (red).
The second case is the one-to-many (1:m) matching relation. This case indicates the fact that a group of features in one dataset, when combined, represents the same object as one feature in the other dataset. This can happen, e.g., when a set of shorter road segments corresponds to a road that is represented as a single line in the other dataset (Figure 2b) or when a road is represented as one line in one dataset but two parallel lines (for the two directions of the road) in the other. The third case of cardinality is the many-to-many matching. This includes two-way one-to-many relations in which one-to-many correspondence exists both from dataset 1 to dataset 2 and, in the opposite direction, from dataset 2 to dataset 1. In addition, the many-to-many case also includes more complicated matchings (Figure 2d) in which no feature individually corresponds to a group of features in the other dataset. Features from the two datasets can only represent the same object in reality after grouping individual features in each dataset, respectively. Some conflation algorithms can handle only the simplest one-to-one conflation problems, while others can handle the more complex one-to-many and many-to-many problems.
Depending on the geometric type of datasets, different methods have been developed for matching point features (e.g. gazettes and points of interests [7]), lines (e.g. transportation networks [8]) and polygons (e.g. building footprints, parcels, census tracts [6]), respectively.
3. Metrics for Conflation
To determine the relations between features, conflation methods typically compute certain metrics of similarity or dissimilarity (distance) between potentially related features. The metrics can be based on the geometry, the attributes (e.g. [7]), and topological relationships of the features involved. Similarity in geometry is a widely used metric, which compares the lengths, shapes and orientations of two features. A general method for computing the geometric difference between two features is the Hausdorff distance. Figure 3 demonstrates the computation of Hausdorff distance. For features A and B, the directed Hausdorff distance from A to B is defined as:
where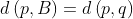 is the distance from a point p
is the distance from a point p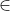 A to the point set B. The directed Hausdorff distance
A to the point set B. The directed Hausdorff distance 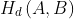 equals the maximum deviation of the points of feature A from feature B. Note that, in practice, the approximate Hausdorff distance is often computed using only the vertices of feature A (instead of all points of A) to save computational time (Figure 3b). In Figure 3, the directed Hausdorff distances from A to B (Figure 3b), and from B to A (Figure 3c) are 40 and 57, respectively. The Hausdorff distance between A and B is 57, the larger of the two directed Hausdorff distances. If A coincides with B or a part of B, obviously
equals the maximum deviation of the points of feature A from feature B. Note that, in practice, the approximate Hausdorff distance is often computed using only the vertices of feature A (instead of all points of A) to save computational time (Figure 3b). In Figure 3, the directed Hausdorff distances from A to B (Figure 3b), and from B to A (Figure 3c) are 40 and 57, respectively. The Hausdorff distance between A and B is 57, the larger of the two directed Hausdorff distances. If A coincides with B or a part of B, obviously 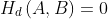 . The Hausdorff distance
. The Hausdorff distance 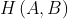 is defined to be the maximum of
is defined to be the maximum of 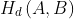 and
and 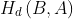 . It is zero only when features A and B equal each other in geometry. Other distance metrics for measuring geometric differences exist.
. It is zero only when features A and B equal each other in geometry. Other distance metrics for measuring geometric differences exist.
Figure 3. Directed Hausdorff distances between a pair of features from two datasets.
Attribute-based metrics compare two features on common attributes such as street names. This can be accomplished, e.g., using string distances such as the Hamming distance or the Levenshtein distance. Topological metrics compare two features based on properties such as the number of edges that enter a node.
4. The Conflation Process
The conflation process typically consists of two main steps: 1) feature matching, and 2) feature merging. In addition, some conflation procedures require a preprocessing step e.g., to adjust the location of features and a post-processing step, e.g. to verify and rectify computer generated match results (and re-run conflation if necessary).
4.1. Feature matching
Given a metric of distance (or dissimilarity) between features (Section 3), a simple strategy of conflation is to match features that are the closest. The k-Closest Pairs Queries (KCPQ) seeks to find k pairs of features whose distances are the smallest [1]. However, such a strategy can be easily disrupted by the spatial displacement of features. In the examples in Figure 1. and the cover image, it can be seen that KCPQ can match some corresponding features correctly, while matching other features incorrectly when these features happen to be close to each other but do not represent the same object in reality.
Another commonly-used conflation method is based on buffer analysis and overlay analysis. For example, the simple buffer method [3] measures the similarity of two features as the percentage of one feature that falls in the buffer of the other. Similar to the distance based KCPQ, the buffer methods require the data to be well aligned before conflation.
The well-known “rubber-sheeting” method was designed in 1980s to deal with unevenly distributed location errors. It was one of the earliest systematic conflation method developed by US Census [9, 11] to conflate USGS data. The method selects a set of counterpart points as “anchors” to link two datasets, in such a way that each triangular region between the anchor points should have similar spatial displacement. The rubber-sheeting method then applies an affine transformation in each region to remove the spatial displacement so that a simpler method such as the buffer method can be applied. The rubber-sheeting method has been extended by researchers and is still in use in many GIS conflation tools nowadays. In general, the method is semi-automatic that can still require significant human intervention in choosing anchor points in the area.
4.2. Feature merging
Once the match relation between features is established properly, the information from corresponding features can be merged following predefined rules. This includes the merging of attribute information and geometry. If the match relation is one-to-one, one can combine attribute information by copying the attributes of one feature to its corresponding feature. If the match relation is one-to-many or many-to-many, an attribute needs to be divided and/or combined and then transferred to the corresponding feature. The rule for the transfer depends on the nature of the attribute. Intensive attributes such as population density may be transferred directly, while extensive attributes such as population count need to be divided before the transfer.
There are also different ways of merging geometries. If one dataset has consistently higher spatial accuracy, one may use its geometries and discard the geometries of the other dataset. If two datasets have similar accuracy, one may compute an “average” geometry between two geometries of a pair of corresponding features. After feature matching and feature merging, one may need to evaluate the accuracy and quality of conflated product by comparing with a small set of conflation results performed by human experts (i.e. ground truth).
5. Discussion
Conflation is closely related to database operations such as spatial join. Both involve combining information in input datasets. However, there are differences between the two processes. First of all, spatial join is a “local” operation based on selecting individual pairs of features satisfying a spatial condition. It is often performed in two stages [4]: 1) a filter stage in which potentially related objects are selected based on indices and bounding rectangles, and 2) a refinement stage that verifies candidate pairs using the full join condition. By comparison, conflation can consider a larger and more complex spatial context and can consider neighboring features, e.g. when using topology based criteria. Secondly, conflation can involve transforming and merging the geometries of the input feature, which typically is not performed during a spatial join.
Geospatial data conflation is also related to the concept of data fusion. In a broader sense, the two terms are sometimes used interchangeably, but data fusion is traditionally more commonly seen in Remote Sensing [10].
Ahmadi, E., & Nascimento, M. A. (2016). K-closest pairs queries in road networks. 17th IEEE International Conference on Mobile Data Management (MDM). DOI: 10.1109/MDM.2016.44
Goodchild, M. F. (2007). Citizens as Sensors: The World of Volunteered Geography. GeoJournal, 69(4), 211-221. DOI: 10.1007/s10708-007-9111-y
Goodchild, M. F., & Hunter, G. J. (1997). A simple positional accuracy measure for linear features. International Journal of Geographical information science, 11(3), 299-306. DOI: 10.1080/136588197242419
Jacox, E. H., & Samet, H. (2007). Spatial join techniques. ACM Transactions on Database Systems (TODS), 32(1), 7. DOI: 10.1145/1206049.1206056
Lei, T. L., & Lei, Z. (2019). Optimal spatial data matching for conflation: A network flow based approach. Transactions in GIS. In press.
Masuyama, A. (2006). Methods for detecting apparent differences between spatial tessellations at different time points. International Journal of Geographical Information Science, 20(6), 633-648. DOI: 10.1080/13658810600661300
McKenzie, G., Janowicz, K., & Adams, B. (2014). A weighted multi-attribute method for matching user-generated Points of Interest. Cartography and Geographic Information Science, 41(2), 125-137. DOI: 10.1080/15230406.2014.880327
Pendyala, R. M. (2002). Development of GIS-based conflation tools for data integration and matching.
Rosen, B., & Saalfeld, A. (1985). Match criteria for automatic alignment. Proceedings of 7th International Symposium on Computer-assisted Cartography (Auto-Carto 7).
Ruiz, J. J., Ariza, F. J., Urena, M. A., & Blázquez, E. B. (2011). Digital map conflation: a review of the process and a proposal for classification. International Journal of Geographical Information Science, 25(9), 1439-1466. DOI: 10.1080/13658816.2010.519707
Saalfeld, A. (1988). Conflation automated map compilation. International Journal of Geographical Information System, 2(3), 217-228.
Obe, R. O., & Hsu, L. S. (2015). PostGIS in action (2nd ed.). Manning Publications Co.
Keywords: