Kriging is an interpolation method that makes predictions at unsampled locations using a linear combination of observations at nearby sampled locations. The influence of each observation on the kriging prediction is based on several factors: 1) its geographical proximity to the unsampled location, 2) the spatial arrangement of all observations (i.e., data configuration, such as clustering of observations in oversampled areas), and 3) the pattern of spatial correlation of the data. The development of kriging models is meaningful only when data are spatially correlated.. Kriging has several advantages over traditional interpolation techniques, such as inverse distance weighting or nearest neighbor: 1) it provides a measure of uncertainty attached to the results (i.e., kriging variance); 2) it accounts for direction-dependent relationships (i.e., spatial anisotropy); 3) weights are assigned to observations based on the spatial correlation of data instead of assumptions made by the analyst for IDW; 4) kriging predictions are not constrained to the range of observations used for interpolation, and 5) data measured over different spatial supports can be combined and change of support, such as downscaling or upscaling, can be conducted.
Author and Citation Info:
Goovaerts, P. (2019). Kriging Interpolation. The Geographic Information Science & Technology Body of Knowledge (4th Quarter 2019 Edition), John P. Wilson (ed.). DOI: 10.22224/gistbok/2019.4.4.
This entry was first published on October 24, 2019.
This Topic is also available in the following editions:
DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Principles of Kriging. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital).
and
DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Kriging Variants. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital).
The kriging method originates from the field of geostatistics. Etymologically, the term “geostatistics” designates the statistical study of natural phenomena. The early developments of geostatistics in the 1950s and 1960s aimed to improve the evaluation of recoverable reserves in mining deposits (Krige, 1951; Journel and Huibregts, 1978). Its field of application expanded considerably to encompass nowadays most fields of geoscience (e.g. geology, geochemistry, geohydrology, soil science) and a vast array of disciplines that deal with the analysis of space-time data, such as oceanography, hydrogeology, remote sensing, agriculture, geography, GIS and environmental sciences.
Most applications of geostatistics are concerned with the prediction of measured attributes at unsampled locations. Consider, for example, the prediction of the value of an attribute z at location u0 using data at five locations, u1 to u5 (Fig. 1).
Figure 1. Two two-dimensional data configurations with different positions for the location u3. In both cases, the prediction at location u0 is accomplished using ordinary kriging and five data at locations u1 to u5. The radius of the dashed circle centered on u0 corresponds to the correlation range. Source: author.
The kriging estimate, denoted z*(u0), is a straightforward linear combination of the five observations:
Equation (1)
The weight assigned to each observation is computed as the solution of the following system of six linear equations that guarantees that the variance of prediction errors is minimum and the estimator is unbiased:
Equation (2)
The 6×6 matrix includes the covariance between any two pairs of data (data-to-data covariance, ), while the right-hand-side (RHS) vector includes the covariance between each observation and the location being predicted (data-to-unknown covariance ). The last equation imposes the unbiasedness constraint that all five weights sum to one, where is a Lagrange parameter. Under the stationarity assumption, the covariance between any two locations and only depends on the distance (and direction if the variability is anisotropic) between these two locations, , a relationship captured by a covariance function, C(h). In practice the spatial dependence of the data is modeled using the semivariogram , and the covariance function is then derived as = C(0)-C(h), where C(0) is the sill of the semivariogram. Let the covariance model be an isotropic spherical model with zero nugget effect, unit sill and a unit range, a, that corresponds to the radius of the dashed circle in Fig. 1:
The kriging system (2) for the data configuration shown in Fig. 1 (left graph) is as follows:
Equation (3)
This system is created by computing the value of the spherical covariance model for the following data-to-data distance matrix and data-to-unknown distance vector:
The large off-diagonal element (C23=0.85, Eq. 3) informs the system of the redundancy of the two data at clustered locations u2 and u3. The RHS vector captures the fact that the first three data are at about the same distance from u0 (i.e., similar covariance), while u4 and u5 are beyond the range of autocorrelation (i.e., C40=C50=0). The solution of system (3) is:
As expected, less weight is assigned to data that are farther away; e.g., u4 and u5. Although u1 and u2 are at the same distance from u0, the latter receives less weight because of its redundancy with the observation u3 (clustering effect). This is an important property not shared by other interpolation methods, such as inverse distance weighting (IDW), as these simpler methods ignore the geometric relationship among observations (e.g., clustering) and only account for the distance between each observation and the unsampled location. In other words, IDW only incorporates the spatial information provided by the RHS vector in Eq. (3), while overlooking the data configuration captured by the left-hand-side matrix. IDW is then particularly ill-suited when observations are spatially clustered.
Another feature of kriging weights is that they can take negative values. For example, simply moving u3 so that it falls between u0 and u2 (Fig. 1, right graph) will lead to the following solution:
Negative weights typically occur when the influence of an observation (i.e., u2 here) is screened by that of a closer one (u3). Negative weights allow the kriging estimate to take values outside the range of the data, which is realistic because there is no reason for the minimum and maximum value in the study area to have been sampled. On the other hand, IDW weights are always positive, resulting in the data being local minimums or local maximums in the interpolated surface (bull’s eye effect). The screening effect also entails that only the closest observations should be used in the prediction because those farther away receive little weight while increasing the size of the kriging system and computational requirements for its solving.
Two extreme situations are: 1) there is no spatial autocorrelation in the dataset, and 2) the location being estimated, u0,coincides with a sampled location . In the first case, all the weights are equal because closer observations do not provide more information; hence, the kriging estimate is the arithmetical average of the observations. In the second case, all weights are zero except for the sampled location, which receives a weight of 1, resulting in a kriging estimate equal to the co-located observation (exactitude property).
For a particular data configuration, kriging weights may drastically change depending on the semivariogram model, which stresses the importance of this preliminary step on the prediction. For the two data configurations of Fig. 1, Fig. 2 shows how the kriging weights change as the nugget effect (NE) represents a larger fraction of the sill (relative NE). In both cases, a larger NE reduces the impact of the data locations (proximity to u0 and screening effect) on the results; the extreme case is a pure NE (i.e., absence of spatial correlation) when all kriging weights are the same, and the kriging estimate is the arithmetical average of the data. For a more thorough discussion of the impact of semivariogram parameters (shape, nugget effect, anisotropy), please refer to Isaaks and Srivastava (1989, p. 296-313).
Figure 2:Impact of the relative nugget effect of the semivariogram model on the kriging weights assigned to each of the five observations in the two data configurations of Fig. 1. Differences between weights decrease as the spatial correlation weakens (i.e., larger nugget effect). Source: author.
In many applications, there is little interest in predicting z at a specific location; instead, the focus is on the value over a bigger spatial support, such as exposure units for soil pollution, management units in agriculture, or blocks for mining. Consider now the problem of estimating the average value of the attribute z over a block V centered at u0 (Fig. 3), an operation referred to as upscaling or aggregation.
Figure 3. Illustration of the problem of kriging a block V centered on location u0 for the first data configuration of Fig. 1. Source: author.
The block value, denoted z(v0), is still estimated as a linear combination of five observations:
Equation (4)
However, the kriging weights are the solution of the following system of equations:
Equation (5)
The only difference between the point-kriging system (Eq. 2) and the block kriging system (Eq. 5) is the RHS vector where the point-to-point covariance is replaced by the point-to-block covariance . In practice, this covariance is estimated by: 1) discretizing the block by using K points uk (e.g., K=4 in the example of Fig. 4A), 2) computing the covariance between and each discretizing point as , where is the distance between and uk, and 3) computing the arithmetical average of these point-to-point covariances. Because point-to-block covariances are estimated by the linear average of point-to-point covariances, the block kriging estimate is equivalent to the average of kriging estimates at K discretizing points (Eq. 1):
Equation (6)
Figure 4. Computation of covariance values for kriging systems that perform change of spatial support. The point-to-block covariance (A) and the block-to-block covariance (B) are approximated by the average of point-to-point covariances computed between points discretizing each block. Source: author.
However, block kriging is computationally more efficient because it requires solving a single block kriging system instead of K point kriging systems.
Point and block kriging can be generalized to the case where all or a fraction of observations are areal data, denoted :
Equations (7) and (8)
Kriging weights are obtained by solving a system of linear equations similar to the one introduced for block kriging, except that block-to-block covariances need to be estimated whenever the two geographical units (i.e., two observations or observation and unsampled location) are blocks. By analogy, with the computation of the point-to-block covariances, such estimation amounts to averaging point-to-point covariances between any two points discretizing the two blocks (Fig. 4B).
Table 1 summarizes all possible combinations in terms of spatial supports for the data and predicted values. Recent methods adopted the more general term “area” instead of “block” to acknowledge the fact that spatial supports can be of any shape and size; e.g., soil units or administrative areas.
Table 1: Terminology of kriging techniques available for all possible combinations of spatial supports for the data (source geography) and the prediction (destination geography).
Data Support
Prediction Support
Point
Areal
Point & Areal
Point
Kriging
Area-to-Point (ATP) kriging
Area-and-Point (AAP) kriging
Area
Block kriging
Area-to-Area (ATA) kriging
Area-and-Point (AAP) kriging
Area-to-Point (ATP) kriging is concerned with the prediction of point values from areal observations and can be viewed as the reverse of block kriging. It performs the operation of downscaling or disaggregation under the constraint that the linear average of all kriging estimates within an area returns the areal value (pycnophylactic interpolation). Examples include the disaggregation of soil units or remote sensing data to create a continuous representation from a choropleth or raster map, respectively.
Area-to-Area (ATA) kriging is concerned with the prediction of areal values from areal observations. It is similar to areal interpolation in the sense that data collected at one set of polygons (the source polygons) are used to predict the data values for a new set of polygons (the target polygons). However, the weight assigned to each source polygon in ATA kriging accounts for the pattern of spatial dependence (i.e., solution of a kriging system) instead of being proportional to the area of each polygon or secondary information, such as population size. Depending on the size of each set of polygons and their geometric relationship (i.e., nested, overlapping), ATA kriging performs the operation of downscaling, upscaling, or side-scaling.
Area-and-Point (AAP) kriging (Goovaerts, 2011) was developed for the situation where observations include both areal and point data, while the prediction is for either a point or a block. Examples include mapping continuous soil attributes using point field data (i.e., carbon measurements) and choropleth maps (e.g., soil or geological maps).
In addition to a predicted value, kriging also provides the attached prediction error variance. For the ordinary kriging estimate (Eq. 1), the kriging variance is computed as:
Equation (9)
As for kriging estimates, two extreme situations are: 1) there is no spatial autocorrelation in the dataset, and 2) the location being estimated, u0,coincides with a sampled location . In the first case, all the data-to-unknown covariances are zero, and the kriging variance is maximum. In the second case, all weights are zero except for the sampled location which receives a weight of 1 and with = = C(0), resulting in a zero kriging variance. In other situations, the kriging variance increases for predictions away from the data and/or as the spatial correlation weakens. It is worth noting that the data values do not appear in Eq. (9), hence two identical data configurations will yield the same kriging variance no matter what the surrounding data are (homoscedasticity). This is a limitation as intuitively the prediction should be much more unreliable if, for example, the five observations range from 1 to 1,000 instead of 1 to 10.
The equations introduced so far relate to the most common type of kriging method, known as “ordinary kriging”. There exists dozens of kriging methods, depending on: 1) the assumption regarding the spatial trend model (constant, unknown, or locally variable), 2) the transformation of data (i.e., lognormal, indicator, or normal score transform), and 3) the use of auxiliary variables in the prediction (e.g., the covariates are sampled at the same locations as the variable of interest, or the covariates are sampled more densely, or they are known everywhere). Interested readers should refer to the following textbooks (Chiles and Delfiner, 1999; Deutsch and Journel, 1998; Goovaerts, 1997; Wackernagel, 1998) for an overview of all these methods.
The application of kriging requires the user to make a series of decisions regarding: 1) the type of kriging method (Section 7), 2) the parameters of the semivariogram model (Section 3), and 3) the way observations are selected (search strategy). The latter is particularly important because using too few observations can create unreliable estimates and artefacts in maps, while using too many observations increases the smoothing of the map. There is no a priori recommended number of data to be used in kriging, and the best way to select this parameter and others is to investigate its impact on prediction accuracy. Such sensitivity analysis can be accomplished by setting some data aside and using the remaining data to make predictions at these test locations while varying the kriging parameters. Prediction errors can then be quantified by comparing predicted and observed values for each combination of parameters, and the combination that minimizes prediction errors should be favored. Note that results can depend on the specific set of test locations, even if they were selected randomly. Thus, ideally the procedure should be repeated for multiple test datasets. For small datasets where discarding data for validation is not an option, one could adopt a leave-one-out approach, whereby one observation is removed at a time and re-estimated from the remaining observations.
References:
Armstrong, M. (1999). Basic Linear Geostatistics, Springer-Verlag, New York.
Chiles, J.P., and Delfiner, P. (1999). Geostatistics: Modeling Spatial Uncertainty, Wiley, New York.
Deutsch, C.V., and Journel, A.G. (1998). GSLIB: Geostatistical Software Library and User's Guide. 2nd edn. New York, Oxford University Press.
Goovaerts, P. (1997). Geostatistics for Natural Resources Evaluation. New York, Oxford University Press.
Goovaerts, P. (2011). A coherent geostatistical approach for combining choropleth map and field data in the spatial interpolation of soil properties. European Journal of Soil Sciences, vol. 62, no.3, pp. 371-380.
Gotway, C.A., and Young, L.J. (2007). A geostatistical approach to linking geographically-aggregated data from different sources. Journal of Computational and Graphical Statistics, vol. 16, no. 1, pp.115-135
Isaaks, E.H., and Srivastava, R.M. (1989). An Introduction to Applied Geostatistics, Oxford University Press, New York.
Journel, A.G., and Huijbregts, C.J. (1978). Mining Geostatistics. New York, Academic Press.
Krige, D.G. (1951). A statistical approach to some basic mine valuation problems on the Witwatersrand. Journal of Chemical, Metallurgical, and Mining Society of South Africa, 52, 119–139.
Kerry, R., Goovaerts, P., Rawlins, B.G. and B.P. Marchant. (2012). Disaggregation of legacy soil data using area to point kriging for mapping soil organic carbon at the regional scale. Geoderma, 170, 347-358.
Kyriakidis, P. (2004). A geostatistical framework for area-to-point spatial interpolation. Geographical Analysis, 36, 259–289.
Montero, J.M., Fernandez-Aviles, G. and J. Mateu. (2015). Spatial and Spatio-Temporal Geostatistical Modeling and Kriging. John Wiley and Sons, NY.
Kriging is an interpolation method that makes predictions at unsampled locations using a linear combination of observations at nearby sampled locations. The influence of each observation on the kriging prediction is based on several factors: 1) its geographical proximity to the unsampled location, 2) the spatial arrangement of all observations (i.e., data configuration, such as clustering of observations in oversampled areas), and 3) the pattern of spatial correlation of the data. The development of kriging models is meaningful only when data are spatially correlated.. Kriging has several advantages over traditional interpolation techniques, such as inverse distance weighting or nearest neighbor: 1) it provides a measure of uncertainty attached to the results (i.e., kriging variance); 2) it accounts for direction-dependent relationships (i.e., spatial anisotropy); 3) weights are assigned to observations based on the spatial correlation of data instead of assumptions made by the analyst for IDW; 4) kriging predictions are not constrained to the range of observations used for interpolation, and 5) data measured over different spatial supports can be combined and change of support, such as downscaling or upscaling, can be conducted.
Goovaerts, P. (2019). Kriging Interpolation. The Geographic Information Science & Technology Body of Knowledge (4th Quarter 2019 Edition), John P. Wilson (ed.). DOI: 10.22224/gistbok/2019.4.4.
This entry was first published on October 24, 2019.
This Topic is also available in the following editions:
DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Principles of Kriging. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital).
and
DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Kriging Variants. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital).
1. Origins of Kriging
The kriging method originates from the field of geostatistics. Etymologically, the term “geostatistics” designates the statistical study of natural phenomena. The early developments of geostatistics in the 1950s and 1960s aimed to improve the evaluation of recoverable reserves in mining deposits (Krige, 1951; Journel and Huibregts, 1978). Its field of application expanded considerably to encompass nowadays most fields of geoscience (e.g. geology, geochemistry, geohydrology, soil science) and a vast array of disciplines that deal with the analysis of space-time data, such as oceanography, hydrogeology, remote sensing, agriculture, geography, GIS and environmental sciences.
2. A Simple Example
Most applications of geostatistics are concerned with the prediction of measured attributes at unsampled locations. Consider, for example, the prediction of the value of an attribute z at location u0 using data at five locations, u1 to u5 (Fig. 1).
Figure 1. Two two-dimensional data configurations with different positions for the location u3. In both cases, the prediction at location u0 is accomplished using ordinary kriging and five data at locations u1 to u5. The radius of the dashed circle centered on u0 corresponds to the correlation range. Source: author.
The kriging estimate, denoted z*(u0), is a straightforward linear combination of the five observations:
The weight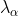 assigned to each observation is computed as the solution of the following system of six linear equations that guarantees that the variance of prediction errors is minimum and the estimator is unbiased:
assigned to each observation is computed as the solution of the following system of six linear equations that guarantees that the variance of prediction errors is minimum and the estimator is unbiased:
The 6×6 matrix includes the covariance between any two pairs of data (data-to-data covariance, ), while the right-hand-side (RHS) vector includes the covariance between each observation and the location being predicted (data-to-unknown covariance
), while the right-hand-side (RHS) vector includes the covariance between each observation and the location being predicted (data-to-unknown covariance  ). The last equation imposes the unbiasedness constraint that all five weights sum to one, where
). The last equation imposes the unbiasedness constraint that all five weights sum to one, where  is a Lagrange parameter. Under the stationarity assumption, the covariance between any two locations
is a Lagrange parameter. Under the stationarity assumption, the covariance between any two locations 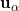 and
and 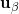 only depends on the distance (and direction if the variability is anisotropic) between these two locations,
only depends on the distance (and direction if the variability is anisotropic) between these two locations,  , a relationship captured by a covariance function, C(h). In practice the spatial dependence of the data is modeled using the semivariogram
, a relationship captured by a covariance function, C(h). In practice the spatial dependence of the data is modeled using the semivariogram 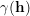 , and the covariance function is then derived as
, and the covariance function is then derived as 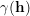 = C(0)-C(h), where C(0) is the sill of the semivariogram. Let the covariance model be an isotropic spherical model with zero nugget effect, unit sill and a unit range, a, that corresponds to the radius of the dashed circle in Fig. 1:
= C(0)-C(h), where C(0) is the sill of the semivariogram. Let the covariance model be an isotropic spherical model with zero nugget effect, unit sill and a unit range, a, that corresponds to the radius of the dashed circle in Fig. 1:
The kriging system (2) for the data configuration shown in Fig. 1 (left graph) is as follows:
This system is created by computing the value of the spherical covariance model for the following data-to-data distance matrix and data-to-unknown distance vector:
The large off-diagonal element (C23=0.85, Eq. 3) informs the system of the redundancy of the two data at clustered locations u2 and u3. The RHS vector captures the fact that the first three data are at about the same distance from u0 (i.e., similar covariance), while u4 and u5 are beyond the range of autocorrelation (i.e., C40=C50=0). The solution of system (3) is:
As expected, less weight is assigned to data that are farther away; e.g., u4 and u5. Although u1 and u2 are at the same distance from u0, the latter receives less weight because of its redundancy with the observation u3 (clustering effect). This is an important property not shared by other interpolation methods, such as inverse distance weighting (IDW), as these simpler methods ignore the geometric relationship among observations (e.g., clustering) and only account for the distance between each observation and the unsampled location. In other words, IDW only incorporates the spatial information provided by the RHS vector in Eq. (3), while overlooking the data configuration captured by the left-hand-side matrix. IDW is then particularly ill-suited when observations are spatially clustered.
Another feature of kriging weights is that they can take negative values. For example, simply moving u3 so that it falls between u0 and u2 (Fig. 1, right graph) will lead to the following solution:
Negative weights typically occur when the influence of an observation (i.e., u2 here) is screened by that of a closer one (u3). Negative weights allow the kriging estimate to take values outside the range of the data, which is realistic because there is no reason for the minimum and maximum value in the study area to have been sampled. On the other hand, IDW weights are always positive, resulting in the data being local minimums or local maximums in the interpolated surface (bull’s eye effect). The screening effect also entails that only the closest observations should be used in the prediction because those farther away receive little weight while increasing the size of the kriging system and computational requirements for its solving.
Two extreme situations are: 1) there is no spatial autocorrelation in the dataset, and 2) the location being estimated, u0, coincides with a sampled location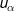 . In the first case, all the weights are equal because closer observations do not provide more information; hence, the kriging estimate is the arithmetical average of the observations. In the second case, all weights are zero except for the sampled location, which receives a weight of 1, resulting in a kriging estimate equal to the co-located observation (exactitude property).
. In the first case, all the weights are equal because closer observations do not provide more information; hence, the kriging estimate is the arithmetical average of the observations. In the second case, all weights are zero except for the sampled location, which receives a weight of 1, resulting in a kriging estimate equal to the co-located observation (exactitude property).
3. Impacts of a Semivariogram Model Specification
For a particular data configuration, kriging weights may drastically change depending on the semivariogram model, which stresses the importance of this preliminary step on the prediction. For the two data configurations of Fig. 1, Fig. 2 shows how the kriging weights change as the nugget effect (NE) represents a larger fraction of the sill (relative NE). In both cases, a larger NE reduces the impact of the data locations (proximity to u0 and screening effect) on the results; the extreme case is a pure NE (i.e., absence of spatial correlation) when all kriging weights are the same, and the kriging estimate is the arithmetical average of the data. For a more thorough discussion of the impact of semivariogram parameters (shape, nugget effect, anisotropy), please refer to Isaaks and Srivastava (1989, p. 296-313).
Figure 2: Impact of the relative nugget effect of the semivariogram model on the kriging weights assigned to each of the five observations in the two data configurations of Fig. 1. Differences between weights decrease as the spatial correlation weakens (i.e., larger nugget effect). Source: author.
4. Block Kriging vs. Point Kriging
In many applications, there is little interest in predicting z at a specific location; instead, the focus is on the value over a bigger spatial support, such as exposure units for soil pollution, management units in agriculture, or blocks for mining. Consider now the problem of estimating the average value of the attribute z over a block V centered at u0 (Fig. 3), an operation referred to as upscaling or aggregation.
Figure 3. Illustration of the problem of kriging a block V centered on location u0 for the first data configuration of Fig. 1. Source: author.
The block value, denoted z(v0), is still estimated as a linear combination of five observations:
However, the kriging weights are the solution of the following system of equations:
The only difference between the point-kriging system (Eq. 2) and the block kriging system (Eq. 5) is the RHS vector where the point-to-point covariance is replaced by the point-to-block covariance
is replaced by the point-to-block covariance  . In practice, this covariance is estimated by: 1) discretizing the block by using K points uk (e.g., K=4 in the example of Fig. 4A), 2) computing the covariance between
. In practice, this covariance is estimated by: 1) discretizing the block by using K points uk (e.g., K=4 in the example of Fig. 4A), 2) computing the covariance between 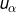 and each discretizing point as
and each discretizing point as  , where
, where  is the distance between
is the distance between 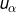 and uk, and 3) computing the arithmetical average of these point-to-point covariances. Because point-to-block covariances are estimated by the linear average of point-to-point covariances, the block kriging estimate
and uk, and 3) computing the arithmetical average of these point-to-point covariances. Because point-to-block covariances are estimated by the linear average of point-to-point covariances, the block kriging estimate 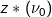 is equivalent to the average of kriging estimates at K discretizing points (Eq. 1):
is equivalent to the average of kriging estimates at K discretizing points (Eq. 1):
Figure 4. Computation of covariance values for kriging systems that perform change of spatial support. The point-to-block covariance (A) and the block-to-block covariance (B) are approximated by the average of point-to-point covariances computed between points discretizing each block. Source: author.
However, block kriging is computationally more efficient because it requires solving a single block kriging system instead of K point kriging systems.
5. Change of Spatial Support
Point and block kriging can be generalized to the case where all or a fraction of observations are areal data, denoted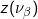 :
:
Kriging weights are obtained by solving a system of linear equations similar to the one introduced for block kriging, except that block-to-block covariances need to be estimated whenever the two geographical units (i.e., two observations or observation and unsampled location) are blocks. By analogy, with the computation of the point-to-block covariances, such estimation amounts to averaging point-to-point covariances between any two points discretizing the two blocks (Fig. 4B).
Table 1 summarizes all possible combinations in terms of spatial supports for the data and predicted values. Recent methods adopted the more general term “area” instead of “block” to acknowledge the fact that spatial supports can be of any shape and size; e.g., soil units or administrative areas.
Area-to-Point (ATP) kriging is concerned with the prediction of point values from areal observations and can be viewed as the reverse of block kriging. It performs the operation of downscaling or disaggregation under the constraint that the linear average of all kriging estimates within an area returns the areal value (pycnophylactic interpolation). Examples include the disaggregation of soil units or remote sensing data to create a continuous representation from a choropleth or raster map, respectively.
Area-to-Area (ATA) kriging is concerned with the prediction of areal values from areal observations. It is similar to areal interpolation in the sense that data collected at one set of polygons (the source polygons) are used to predict the data values for a new set of polygons (the target polygons). However, the weight assigned to each source polygon in ATA kriging accounts for the pattern of spatial dependence (i.e., solution of a kriging system) instead of being proportional to the area of each polygon or secondary information, such as population size. Depending on the size of each set of polygons and their geometric relationship (i.e., nested, overlapping), ATA kriging performs the operation of downscaling, upscaling, or side-scaling.
Area-and-Point (AAP) kriging (Goovaerts, 2011) was developed for the situation where observations include both areal and point data, while the prediction is for either a point or a block. Examples include mapping continuous soil attributes using point field data (i.e., carbon measurements) and choropleth maps (e.g., soil or geological maps).
6. Kriging Variance
In addition to a predicted value, kriging also provides the attached prediction error variance. For the ordinary kriging estimate (Eq. 1), the kriging variance is computed as:
As for kriging estimates, two extreme situations are: 1) there is no spatial autocorrelation in the dataset, and 2) the location being estimated, u0, coincides with a sampled location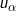 . In the first case, all the data-to-unknown covariances
. In the first case, all the data-to-unknown covariances  are zero, and the kriging variance is maximum. In the second case, all weights are zero except for the sampled location which receives a weight of 1 and with
are zero, and the kriging variance is maximum. In the second case, all weights are zero except for the sampled location which receives a weight of 1 and with  =
=  = C(0), resulting in a zero kriging variance. In other situations, the kriging variance increases for predictions away from the data and/or as the spatial correlation weakens. It is worth noting that the data values do not appear in Eq. (9), hence two identical data configurations will yield the same kriging variance no matter what the surrounding data are (homoscedasticity). This is a limitation as intuitively the prediction should be much more unreliable if, for example, the five observations range from 1 to 1,000 instead of 1 to 10.
= C(0), resulting in a zero kriging variance. In other situations, the kriging variance increases for predictions away from the data and/or as the spatial correlation weakens. It is worth noting that the data values do not appear in Eq. (9), hence two identical data configurations will yield the same kriging variance no matter what the surrounding data are (homoscedasticity). This is a limitation as intuitively the prediction should be much more unreliable if, for example, the five observations range from 1 to 1,000 instead of 1 to 10.
7. Kriging Variants
The equations introduced so far relate to the most common type of kriging method, known as “ordinary kriging”. There exists dozens of kriging methods, depending on: 1) the assumption regarding the spatial trend model (constant, unknown, or locally variable), 2) the transformation of data (i.e., lognormal, indicator, or normal score transform), and 3) the use of auxiliary variables in the prediction (e.g., the covariates are sampled at the same locations as the variable of interest, or the covariates are sampled more densely, or they are known everywhere). Interested readers should refer to the following textbooks (Chiles and Delfiner, 1999; Deutsch and Journel, 1998; Goovaerts, 1997; Wackernagel, 1998) for an overview of all these methods.
8. Validating a Kriging Model
The application of kriging requires the user to make a series of decisions regarding: 1) the type of kriging method (Section 7), 2) the parameters of the semivariogram model (Section 3), and 3) the way observations are selected (search strategy). The latter is particularly important because using too few observations can create unreliable estimates and artefacts in maps, while using too many observations increases the smoothing of the map. There is no a priori recommended number of data to be used in kriging, and the best way to select this parameter and others is to investigate its impact on prediction accuracy. Such sensitivity analysis can be accomplished by setting some data aside and using the remaining data to make predictions at these test locations while varying the kriging parameters. Prediction errors can then be quantified by comparing predicted and observed values for each combination of parameters, and the combination that minimizes prediction errors should be favored. Note that results can depend on the specific set of test locations, even if they were selected randomly. Thus, ideally the procedure should be repeated for multiple test datasets. For small datasets where discarding data for validation is not an option, one could adopt a leave-one-out approach, whereby one observation is removed at a time and re-estimated from the remaining observations.
Armstrong, M. (1999). Basic Linear Geostatistics, Springer-Verlag, New York.
Chiles, J.P., and Delfiner, P. (1999). Geostatistics: Modeling Spatial Uncertainty, Wiley, New York.
Deutsch, C.V., and Journel, A.G. (1998). GSLIB: Geostatistical Software Library and User's Guide. 2nd edn. New York, Oxford University Press.
Goovaerts, P. (1997). Geostatistics for Natural Resources Evaluation. New York, Oxford University Press.
Goovaerts, P. (2011). A coherent geostatistical approach for combining choropleth map and field data in the spatial interpolation of soil properties. European Journal of Soil Sciences, vol. 62, no. 3, pp. 371-380.
Gotway, C.A., and Young, L.J. (2007). A geostatistical approach to linking geographically-aggregated data from different sources. Journal of Computational and Graphical Statistics, vol. 16, no. 1, pp.115-135
Isaaks, E.H., and Srivastava, R.M. (1989). An Introduction to Applied Geostatistics, Oxford University Press, New York.
Journel, A.G., and Huijbregts, C.J. (1978). Mining Geostatistics. New York, Academic Press.
Krige, D.G. (1951). A statistical approach to some basic mine valuation problems on the Witwatersrand. Journal of Chemical, Metallurgical, and Mining Society of South Africa, 52, 119–139.
Kerry, R., Goovaerts, P., Rawlins, B.G. and B.P. Marchant. (2012). Disaggregation of legacy soil data using area to point kriging for mapping soil organic carbon at the regional scale. Geoderma, 170, 347-358.
Kyriakidis, P. (2004). A geostatistical framework for area-to-point spatial interpolation. Geographical Analysis, 36, 259–289.
Montero, J.M., Fernandez-Aviles, G. and J. Mateu. (2015). Spatial and Spatio-Temporal Geostatistical Modeling and Kriging. John Wiley and Sons, NY.
Wackernagel, H. (1998). Multivariate Geostatistics, 2nd Completely Revised Edition. Springer, Berlin.
Webster R., and Oliver M.A. (2001). Geostatistics for Environmental Scientists. John Wiley and Sons, West Sussex, England.
Keywords: