Distance decay is an essential concept in geography. At its core, distance decay describes how the relationship between two entities generally gets weaker as the separation between them increases. Inspired by long-standing ideas in physics, the concept of distance decay is used by geographers to analyze two kinds of relationships. First, the term expresses how measured interactions (such as trade volume or migration flow) generally decrease as the separation between entities increases, as is analyzed by spatial interaction models. Second, the term is used to describe how the implicit similarity between observations changes with separation, as measured by variograms. For either type of relationship, we discuss how "separation" must be clearly articulated according to the mechanism of the relationship under study. In doing this, we suggest that separation need not refer to positions in space or time, but can involve social or behavioral perceptions of separation, too. To close, we present how the "death of distance" is transforming distance decay in uneven ways.
Author and Citation Info:
Hasova, L. and Wolf, L. J. (2022). Proximity and Distance Decay. The Geographic Information Science & Technology Body of Knowledge (2nd Quarter 2022 Edition). John P. Wilson (Ed.). DOI: 10.22224/gistbok/2022.2.3.
This topic is also available in an earlier edition:
DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Proximity and distance decay. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital).
distance decay: the relationship between two entities decreases as the separation between them increases. gravity model: a long-standing theoretical model that predicts an explicitly measured interaction, such as trade or migration, as a function of separation. variogram: an empirical construct used to measure distance decay in similarity among measurements in geographical data. travel cost: a method of defining separation that emphasizes how separation is often measured in terms of what is spent to move between destinations.
Distance decay is a common phenomenon in social, economic, and natural systems. It is also a fundamental concept in geography. Distance decay describes how the strength of a relationship between people, places, or systems decreases as the separation between them increases. The strength of relationship is usually some kind of measured interaction or implicit similarity between entities in a spatial process. For interaction, we often think of trade between countries or social networks between friends in a city. For similarity, we might think of how the temperature in your front yard is nearly identical to that of your next-door neighbor's. Separation, then, is usually defined according to the relationship being studied. For example, if the relationship being studied is trade between countries, a relevant separation could reflect the total cost of sending a shipping container between countries. But, to understand the similarity of temperature between parts of a city, straight-line/Euclidean distance may suffice. Our definition of "distance decay" uses these abstract concepts of relation and separation, though, to allow for the many alternative definitions that emerge in geography. Even though the rise and intensification of information technology has radically transformed how distance is experienced in social systems, distance decay still emerges in useful ways for both theories of interaction and empirical measures of similarity.
In the following sections, we discuss theses two senses of distance decay. We present a theoretical model of distance decay in interaction, the gravity model, and an empirical measure of distance decay in similarity, the variogram. We close by discussing how alternative notions of separation can be useful in more general contexts, too.
Distance decay is one of the oldest concepts in geography. The effect of distance on social interaction phenomena was recognized in late 19th century, when Ravenstein (1885) examined migration in the British Isles. Although Ravenstein only used "the simplest form of arithmetic" (Tobler, 1995), his observations that emigrants from Ireland largely moved to the closest county in Great Britain (p.177) inspired future researchers to investigate this relationship between interaction (as migration) and distance. Debate continues about Ravenstein's "proper" role in this, however. Grigg (1977) notes Ravenstein's interest in distance decay, but also claims "[Ravenstein] made no explicit discussion of the influence of distance." (p.46), and indeed Ravenstein only refers to "border effects" and "nearest neighbors" in his discussion while also emphasizing the decidedly non-local appeal of "London, Lancashire, and the West Riding."
An example of this is in Figure 1, which shows migration out of the London ward of Islington. In this image, darker colors indicate a greater number of migrants from Islington. Thus, the map shows that people who leave Islington tend to move to places near Islington, rather than to more distant locales. This principle was later explored by Reilly (1931), who developed an explicit specification of distance decay for migration models, and was then applied to trade flows by Isard (1954), flows of information by Gould and White (1985), and now sees extensive application for many different kinds of interaction (Oshan, 2021).
Figure 1. Out-migration from the central London borough of Islington. Darker colors indicate more families have moved from Islington to other boroughs in and around London, showing that people in Islington are more likely to move to closer boroughs than more distant boroughs. Map tiles by Stamen Design, under CC BY 3.0. Data by OpenStreetMap, under ODbL. Source: authors.
In this sense, distance decay refers to interactions that we directly measure and predict to decrease as distance increases. Separation is one predictor of interaction, possibly among many others. Together, this means that distance decay, the existence and strength of a negative relationship between separation and interaction, is a core question in this literature.
As a reflection of this, most studies in this literature all share the same basic traits that stem from their adaptation of (or reaction to) properties of distance decay in physics, which will be discussed in Section 3.1. Specifically, distance decay is usually expected to"exist;" in some sense. If it does not, then the model is assumed to be incorrectly specified, distance in-artfully measured, or parameters incorrectly estimated. Thus, in this spatial interaction modelling perspective, distance decay is a theoretical construct embedded in models that may "hold" to varying degrees.
While spatial interaction models were being formalized, empirical interest in distance decay in similarity was also growing. For example, Stephan (1934), was concerned that most statistical analyses ignored how nearby census tracts tended to have similar sociodemographic characteristics. The chief concern was not about explicit interaction between census tracts, but rather an implicit similarity between tracts that decayed with distance. To measure this, Matheron (1963) developed the variogram, which describes the distance decay in covariation for geographic measurements. In most geographic analyses, co-variation does tend to decrease as separation between measurements increases. However, this is not always the case, and there is often something useful revealed about the process generating the data when distance decay in similarity does not hold (Griffith, 2019). Thus, work using the variogram has become widespread in both social and physical sciences, driven by how useful the variogram (and related tools and concepts) are in describing and controlling for the statistical effects of distance decay in the similarity of measurements.
Thus, "distance decay" as used by geographers refers to one of these two relationships: either similarity implicit in the structure of geographic data (i.e. measured by a variogram) or interactions explicit between geographic entities (i.e. modeled by a spatial interaction model). Thus, these two senses of "distance decay" reflect separate perspectives for how distance decay emerges in geography (Wolf et al., 2020). The following sections discuss these two perspectives in detail, illustrating their fundamental similarities and showing how separation or relation may change, but distance decay will likely remain.
3.1 Distance Decay in Interaction: the Gravity Model
At its core, spatial interaction models seek to predict the interaction between two entities, like trade between countries, migration between regions, or instant messages between friends. The interaction (sometimes also called a "flow" in trade or migration studies) originates somewhere (we'll call this site the origin, i) and ends up somewhere else (the destination, j). This flow is is denoted fij.
Then, interaction models predict the size of each flow using three factors. First, "pull" factors (sometimes called "attractiveness," Aj) encourages agents to interact with a destination j. As a complement, the "push" factors (known also as "propulsiveness," spelled Pj) encourage interaction from an origin. These are generally different for different places, and will be defined differently problem-to-problem depending on the interaction being studied. For example, in studies of migration, a push factor might be an economic collapse or invasion in possible origin countries, while pull factors might be low unemployment or high standards of living in possible destination countries.
Figure 2. Distance decay functions for a gravity model of spatial interaction from Equation 1. Four different values of ß are shown to indicate different "speeds" of distance decay. For a small value of ß = - 0.1, interaction between an origin and a destination decays very slowly they get further apart. For a larger value of ß = -1, interaction decays very quickly. Source: authors.
The next part of the classic interaction model is a measure of distance between i and j, generally spelled dij. Again, this may be a physical distance, or may be measured using a more abstract notion of "separation." We will discuss this in more detail later.
Finally, to assemble the model, we need to weight each of these factors according to how important they are in generating interaction. Unfortunately, the proper values of these weights are unknown, so they have to be estimated from interaction data. Here, we use Greek symbols to stand-in for these unknown values: reflects an unknown "baseline" level of interaction, adjusts the importance of attractiveness Ak, adjusts propulsiveness, and reflects the importance of distance to flow. The gravity model of spatial interaction brings these factors together to predict interaction:
(Equation 1)
All of the unknown values () have to be estimated from the data, and the values of will depend on the structure of the push and pull factors. However, a negative estimate of ß is usually obtained from the data, suggesting that interaction between i and j decreases as distance increases. Indeed, a large literature focuses on understanding and adjusting for things that might "confound" distance decay, causing ß estimates to be positive and implying interaction increases with distance. See Oshan (2021) for a detailed discussion. As a result, contemporary analyses of interaction may use more sophisticated models that control for confounding effects (such as accessibility (Fotheringham, 1983)) and yield ß estimates that represent distance decay.
The structure of this decay is quite flexible in practice. Figure 2 shows three values of ß where the expected interaction strength (on the vertical axis) is plotted against the distance between origins and destinations (on the horizontal axis). All interaction fades as separation increases, but interaction decays more quickly as gets more negative. Alternatively, Figure 3 shows how different shapes of distance decay functions will "spread" interaction differently. The standard "power" decay function (used in Eq. 1, for example) will tend to predict that interactions between observations are highly concentrated among the closest pairs, while a linear decay will spread interactions out over more distant pairs.
Figure 3. Three distance decay functions that "spread" interaction differently among observations. The "power" decay function is generally the most concentrated, while linear (or logarithmic forms, not pictured) are the least concentrated. Source: authors.
Unfortunately, deciding how to measure "distance" or what form of "decay" to use can be quite difficult. Theoretical arguments about the form of decay suggest that the importance of distance decreases with the size of the trip (Haggett, 1979). For example, a walk that takes ten minutes will be fairly disrupted by a detour that takes ten extra minutes, but the same detour will matter much less in a three-hour trek. But, this might not be the same in all processes. Therefore, choosing between forms of distance decay is often a data-intensive process where many models are fit with different distance decay functions, and then compared based on their predictive ability.
In addition to the strength and the form of decay, the measurement of separation is also quite important. We have avoided this topic so far because it can be very complex. Note that the detour example above expressed distance in terms of time, not space. Other kinds of distance may not refer to space-time locations at all! Therefore, given its theoretical importance, we dedicate an entire section later to thinking about how to measure "distance" in distance decay, and discuss the social and material forces that are re-shaping distance itself.
3.2 Distance Decay in Similarity: the Variogram
Distance decay is also used in geography to refer to how nearby things tend to be more similar than distant things. This distance decay in similarity is intimately related to the idea of spatial autocorrelation, which applies in a much more general sense than the distance decay we see in interaction. This is because distance decay in similarity is not limited to studies of interaction (like trade, social networks, or migration), and so is frequently used to describe any set of geographic measurements. So, let us consider one of the most common ways of thinking about distance decay in similarity: the variogram.
At its most basic, the variogram measures the similarity between pairs of observations separated by a given distance. Variograms define similarity as the variance of the differences between measurements. It calculates this variance for sets of sites separated by some distance, h. For now, let us assume that we have some number of sites Nh that are separated exactly by h, meaning dij = h. Then, the value of the variogram for distance h, spelled , is defined as the sum of squared differences between pairs of sites i, j that are separated by exactly h:
(Equation 2)
In this instance, we can compute for any separation h, and plot the value of this function as h goes from describing very close measurements to very distant measurements. In practice, we usually compute ) for pairs of observations separated by approximately h. For example, if h = 2 kilometers, we might use pairs of observations separated by between 1.8 and 2.2 kilometers. This is because there are only a xed number of observation pairs, but infinitely many values of h for which the variogram has to be evaluated. A "best fit" curve is usually estimated to describe the shape of computed values of . As in spatial interaction models, the form of this curve is flexible. Regardless of this form, large values of indicate that observations separated by distance h are very different, and small values of indicate that they are very similar. So, the faster the variogram increases, the stronger the distance decay in similarity. Figure 4 shows this for many different "ranges," or separations at which the variogram attains its "stable" long-run value (called the "sill").
Figure 4.Three variograms plotted from simulated data. Three different "ranges" are shown that influence the speed of distance decay. The variogram with fastest distance decay reaches its stable long-run value (the "sill") first. Source: authors.
For variograms (and other related methods), distance decay means that similarity between measurements decreases as separation increases. Because variograms are not limited to studying distance decay in geographic data about interactions, they are widely used and heavily customized. As a consequence, many methods build upon the basic premise of the variogram. For example, spatial correlograms measure similarity using the correlation between pairs of values separated by a given distance. Alternatively, some scholars build variograms for distances in an ordinal sense, computing similarity among some number of nearest neighbors to each measurement. As is the case with gravity models in spatial interaction, variograms are only one part of a broad and flexible framework used throughout geographical analysis.
In previous sections, we have examined how distance decay is used and analyzed in two different senses. In both cases, distance decay describes how a kind of relationship gets smaller as the separation between things gets larger. However, spatial interaction models think of "relationship" as some kind of interaction that we directly measure, while variograms think of "relationship" as an implicit similarity between measurements. We also discussed how different mathematical forms can change how decay is distributed among pairs of observations.
This leaves one last term undefined: how should we measure "separation"? The previous sections simply referred to a "distance" or "separation," and did not specify how this was to be measured. This section will provide more detail on how separation may (or may not) be usefully defined and measured, as well as discuss how new technological and social developments affect how we conceptualize distance. Most of this discussion refers explicitly to ideas of distance decay in interaction, since these are questions where the presence (or absence) of distance decay is directly under study in a measurement of interaction. However, more abstract notions of distance and the \death of distance" affect studies of distance decay in separation, too.
4.1 Measuring Distance in Space and Time
Our initial definition of distance decay used the term "separation" to indicate that "distance" may need to be defined in very abstract ways for social or economic processes. Put simply, distance decay in a process might not be apparent if you use straight-line (a.k.a. "Euclidean") distance. In a very basic sense, humans live on a curved Earth; straight-line distance distorts this, and it is more accurate to measure distances using paths along the surface of a curved and bumpy planet. But, this is only one way that simple physical ideas of distance fail to capture our complex socially mediated reality. Paths that interactions take from their origins to their destinations are rarely straight, and often involve changes in the mode of travel. For example, a migrant might take a train to an airport, fly north to a layover, and then east to their final destination. Together, this implies a more abstract socially-mediated notion of distance, called travel cost, that reflects how expensive interaction is using some common resource like time or money. Travel cost definitions of separation have long been used to study distance decay (e.g. Harris, 1954), but can be very hard to measure or represent. In urban contexts (for example), some individuals prefer to chose paths that take less time (time costs), are straighter (turn costs), less expensive (monetary costs), more environmentally friendly (climate costs), or involve fewer changes between modes of transit (transfer costs). The considerations that any agent might make is too nebulous to be useful, so travel costs are usually measured using a weighted combination of a limited set of costs.
This method of analysis only gets us so far, however. Travel cost can vary from person to person, and individuals might strongly disagree about the "cost" of a route because they weight costs differently from one another. Costs may depend on the context in which actors make decisions (Eldridge and Jones III, 1991; Fotheringham, 1983). This means that the structure of travel costs can change within a system, or distance decay itself can behave differently depending on where in the system it is studied. Travel costs can also change over time, as individuals' judgments evolve or systems of transport are transformed. Thus, while a physical distance between two places may be fairly consistent, the relevant socially-mediated travel costs can and do vary widely between people, places, and times.
4.2 Beyond Space and Time Distance Decay
Going further, distance decay can even apply in situations where neither physical nor travel distance matters. Instead, behavioral or social measures of relation may be important when understanding how people move through their city or select where they want to live. Foundational work in geography shows that individuals perceive space in ways that may not map very well to physical or travel definitions of separation (Gould and White, 1985; Golledge and Hubert, 1982). For example, people may think of familiar or more desirable destinations as "closer," regardless of travel cost or distance. This more subjective notion of separation undoubtedly affects the way individuals reason about interaction, and thus affects how distance decay works in practice.
Alternatively, social or economic similarity itself can act as a separation over which distance decay acts (Gatrell, 1983). As an example, the idea of homophily in sociology describes how contact between similar people is more common than contact between dissimilar people (McPherson et al., 2001). Here, distance is defined as a social separation reflecting the demographic or psychological dissimilarity between people. In this case, as social separation between people increases, their interactions decrease - a social distance decay.
This removes the idea of distance decay from space and time entirely. As in our discussion of the two most common definitions of "relation," decisions about how to define "distance" or "relation" will determine how distance decay is made meaningful in a given study. This, in turn, structures any inquiry into distance decay itself. Therefore, it is important to critically articulate and defend the mechanism (or mechanisms) by which separation affects the relationships under study, and then measure separation and relation as accurately as possible.
4.3 The Present and Future Transformations of Distance Decay
As a consequence of the socially-mediated (and at times deeply personal) nature of separation, the way that distance "works" has changed substantially over time. This has been well-studied in historical work on economic geography and the urban system (Borchert, 1967). The continued relevance of distance (and, as a consequence, the existence of distance decay) is seriously debated today.
Some have speculated that physical distance is becoming less important because of the rise of online interaction (Cairncross, 2001). An instant message is approximately instant, whether you talk to your next-door neighbor or someone on the other side of the world. As a behavioral example, Lendle et al. (2016) shows that the internet supplants consumers' local knowledge networks. This decreases the importance of nearby people and/or marketplaces in learning about products and thus weakens distance decay in consumer interactions with sellers. Thus, the power of distance decay may weaken in consumer decision-making.
Ultimately, however, distance decay remains strong in many social processes. The death of distance (decay) in studies of urban transit systems may be less radical than anticipated (Rietveld and Vickerman, 2004). For studies in trade, Buch et al. (2004) discusses the "distance puzzle": even as transportation costs have been slashed dramatically (in part due to digital technologies), estimates of the strength of distance decay in trade remain stable. Buch et al. (2004) finds that this is because spatial interaction models estimate distance decay as a relative propensity for "near" things to interact more than "distant" things, not as an absolute determinant of interaction. Distant trade partners still pay more transit costs than near trade partners even though everyone pays less overall. Thus, despite the "death of distance," distance decay still exists.
Another contemporary debate about distance decay focuses on the COVID-19 pandemic. Because of "stay at home" orders and the attendant rise in remote working, some believe we are seeing structural changes in workforce composition may accelerate the "death of distance." However, there are good conceptual reasons to believe that distance decay will remain important in peoples' location and consumption decisions (Reades and Crookston, 2021). Indeed, as the internet increasingly mediates human interaction, distance decay is still quite strong according to digitally-relevant notions of separation (Couclelis, 1996; Tranos and Nijkamp, 2013). Distance decay may increase in relevance for human geography, but with digitally- or socially-mediated distances playing an increasingly important role. However, these structural changes in the geographic patterns of work and residence are still evolving rapidly as the COVID-19 pandemic evolves, so the ultimate effect of these changes remain unclear (Rose-Redwood et al., 2020).
Distance decay is a fundamental concept in geography. At its core, distance decay describes how the relationships between entities get weaker as separation increases; nearer things will tend to be more related than distant things. In practice, this applies both to cases where we see the relationships directly (like trade or migration), and cases where the relationships are only indirectly measured. We discuss how the gravity model of spatial interaction and the variogram represent these two cases, respectively. Both senses of distance decay are important to understand, as either (or both) are present in many processes. We discuss how the idea of "distance" may be more than physical, reflecting socially-mediated travel costs, individual perceptions of distance, or socioeconomic similarity. In addition to being one of the oldest concepts in geographic analysis, distance decay will remain relevant even as new technologies and world events transform how distance is experienced.
References:
Borchert, J. R. (1967). American Metropolitan Evolution. Geographical Review, 57(3):301. doi: 10.2307/212637.
Buch, C. M., JKleinert, J., and Toubal, F. (2004). The distance puzzle: on the interpretation of the distance coefficient in gravity equations. Economics Letters, 83(3):293-298. doi: 10.1016/j.econlet.2003.10.022.
Cairncross, F. (2001). The Death of Distance: How the Communications Revolution Is Changing Our Lives. Harvard Business School Press, Boston.
Couclelis, H. (1996). The Death of Distance. Environment and Planning B: Planning and Design, 23(4):387-389, August 1996. doi: 10.1068/b230387.
Eldridge, J. D. and Jones III, J. P. (1991). Warped Space: A Geography of Distance Decay. The Professional Geographer, 43(4):500-511. doi: 10.1111/j.0033-0124.1991.00500.x.
Fotheringham, A. S. (1983). A New Set of Spatial-Interaction Models: The Theory of Competing Destinations. Environment and Planning A: Economy and Space, 15:15-36.
Gatrell, A. C. (1983). Distance and space: a geographical perspective. Oxford University Press, USA.
Golledge, R. G., and L J Hubert, L. J. (1982). Some Comments on Non-Euclidean Mental Maps. Environment and Planning A: Economy and Space, 14(1):107-118. doi:10.1068/a140107.
Gould, P. and White, R. (1985). Mental Maps. Penguin Books, Hoboken.
Griffith, D. A. (2019). Negative Spatial Autocorrelation: One of the Most Neglected Concepts in Spatial Statistics. Stats, 2(3):388-415. doi: 10.3390/stats2030027. https://www.mdpi.com/2571-905X/2/3/27.
Grigg, D. B. (1977). E.G. Ravenstein and the "laws" of migration. Journal of Historical Geography, 3:41-54,1977.
Haggett, P. (1979). Geography: a modern synthesis. Harper & Row series in geography. Harper and Row, New York ; London, 3rd ed. edition.
Harris, C. D. (1954). The Market as a Factor in the Localization of Industry in the United States. Annals of the Association of American Geographers, 44(4):315-348. doi: 10.2307/2561395.
Isard, W.. Location theory and trade theory: Short-run analysis. Quarterly Journal of Economics, 68:305-320, 1954.
Lendle, A., Olarreaga, M., Schropp, S., and Vezina, P-L. (2016). There Goes Gravity: eBay and the Death of Distance. The Economic Journal, 126(591):406-441. doi: 10.1111/ecoj.12286.
Matheron, G. (1963). Principles of geostatistics. Economic Geology, 58:1246-1266.
McPherson, M., Smith-Lovin, L., and Cook, J. M. (2001). Birds of a Feather: Homophily in Social Networks. Annual Review of Sociology, 27(1):415-444.
Oshan, T. M. (2021). The spatial structure debate in spatial interaction modeling: 50 years on. Progress in Human Geography, 45(5):925-950. doi: 10.1177/0309132520968134.
Ravenstein, E. G. (1885). The laws of migration. Journal of the Statistical Society of London, 48:167-235.
Reades, J. and Crookston, M. (2021). Why Face-to-Face Still Matters: The Persistent Power of Cities in the Post-Pandemic Era. Policy Press. Google-Books-ID: YI8kEAAAQBAJ.
Reilly, W. J. (1931). The law of retail gravitation. Knickerbocker Press.
Rietveld, P. and Roger Vickerman. (2004). Transport in regional science: The "death of distance" is premature*. Papers in Regional Science, 83(1):229-248, 2004. doi: 10.1007/s10110-003-0184-9.
Rose-Redwood, R., Rob Kitchin, Elia Apostolopoulou, Lauren Rickards, Tyler Blackman, Jeremy Crampton, Ugo Rossi, and Michelle Buckley. (2020). Geographies of the COVID-19 pandemic. Dialogues in Human Geography, 10(2):97-106.. doi: 10.1177/2043820620936050.
Stephan, F. F. (1934). Sampling Errors and Interpretations of Social Data Ordered in Time and Space. Journal of the American Statistical Association, 29(185A):165-166. doi: 10.1080/01621459.1934.10506245.
Tobler, W. R. (1995). Migration: Ravenstein, Thornthwaite, and beyond. Urban Geography, 16:327-343. doi: 10.2747/0272-3638.16.4.327.
Tranos. E. and Nijkamp. P. (2013). The Death of Distance Revisited: Cyber-Place, Physical and Relational Proximities. Journal of Regional Science, 53(5):855-873. doi: 10.1111/jors.12021.
Wolf, L. J., Sean Fox, Rich Harris, Ron Johnston, Kelvyn Jones, David Manley, Emmanouil Tranos, and Wenfei Winnie Wang. (2020). Quantitative geography III: Future challenges and challenging futures. Progress in Human Geography, page 0309132520924722 . doi: 10.1177/0309132520924722.
Learning Objectives:
Explain the history of distance decay as a concept in geography
Distinguish the kind of relationship being measured (such as interaction or similarity) in analyses of distance decay
Interpret estimates of the strength of distance decay in spatial interaction models
Compare the properties of variograms graphically
Explain how distance decay may use more notions of \separation" that are relevant in geographic analysis, including travel costs, perceived distance, or socio-economic distance.
Instructional Assessment Questions:
What physical (or social) processes were influential in geographers' thinking about distance decay?
What kinds of processes might exhibit very dramatic (that is, \fast") distance decay? What processes might not exhibit distance decay at all?
What kinds of social processes might be well represented by the gravity model of spatial interaction? Which may not?
Distance is important when measuring or modelling distance decay. What kinds of interaction costs do you experience in your daily life?
Distance decay is an essential concept in geography. At its core, distance decay describes how the relationship between two entities generally gets weaker as the separation between them increases. Inspired by long-standing ideas in physics, the concept of distance decay is used by geographers to analyze two kinds of relationships. First, the term expresses how measured interactions (such as trade volume or migration flow) generally decrease as the separation between entities increases, as is analyzed by spatial interaction models. Second, the term is used to describe how the implicit similarity between observations changes with separation, as measured by variograms. For either type of relationship, we discuss how "separation" must be clearly articulated according to the mechanism of the relationship under study. In doing this, we suggest that separation need not refer to positions in space or time, but can involve social or behavioral perceptions of separation, too. To close, we present how the "death of distance" is transforming distance decay in uneven ways.
Hasova, L. and Wolf, L. J. (2022). Proximity and Distance Decay. The Geographic Information Science & Technology Body of Knowledge (2nd Quarter 2022 Edition). John P. Wilson (Ed.). DOI: 10.22224/gistbok/2022.2.3.
This topic is also available in an earlier edition:
1. Definitions
distance decay: the relationship between two entities decreases as the separation between them increases.
gravity model: a long-standing theoretical model that predicts an explicitly measured interaction, such as trade or migration, as a function of separation.
variogram: an empirical construct used to measure distance decay in similarity among measurements in geographical data.
travel cost: a method of defining separation that emphasizes how separation is often measured in terms of what is spent to move between destinations.
2. Introduction
Distance decay is a common phenomenon in social, economic, and natural systems. It is also a fundamental concept in geography. Distance decay describes how the strength of a relationship between people, places, or systems decreases as the separation between them increases. The strength of relationship is usually some kind of measured interaction or implicit similarity between entities in a spatial process. For interaction, we often think of trade between countries or social networks between friends in a city. For similarity, we might think of how the temperature in your front yard is nearly identical to that of your next-door neighbor's. Separation, then, is usually defined according to the relationship being studied. For example, if the relationship being studied is trade between countries, a relevant separation could reflect the total cost of sending a shipping container between countries. But, to understand the similarity of temperature between parts of a city, straight-line/Euclidean distance may suffice. Our definition of "distance decay" uses these abstract concepts of relation and separation, though, to allow for the many alternative definitions that emerge in geography. Even though the rise and intensification of information technology has radically transformed how distance is experienced in social systems, distance decay still emerges in useful ways for both theories of interaction and empirical measures of similarity.
In the following sections, we discuss theses two senses of distance decay. We present a theoretical model of distance decay in interaction, the gravity model, and an empirical measure of distance decay in similarity, the variogram. We close by discussing how alternative notions of separation can be useful in more general contexts, too.
3. Two Senses of Distance Decay
Distance decay is one of the oldest concepts in geography. The effect of distance on social interaction phenomena was recognized in late 19th century, when Ravenstein (1885) examined migration in the British Isles. Although Ravenstein only used "the simplest form of arithmetic" (Tobler, 1995), his observations that emigrants from Ireland largely moved to the closest county in Great Britain (p.177) inspired future researchers to investigate this relationship between interaction (as migration) and distance. Debate continues about Ravenstein's "proper" role in this, however. Grigg (1977) notes Ravenstein's interest in distance decay, but also claims "[Ravenstein] made no explicit discussion of the influence of distance." (p.46), and indeed Ravenstein only refers to "border effects" and "nearest neighbors" in his discussion while also emphasizing the decidedly non-local appeal of "London, Lancashire, and the West Riding."
An example of this is in Figure 1, which shows migration out of the London ward of Islington. In this image, darker colors indicate a greater number of migrants from Islington. Thus, the map shows that people who leave Islington tend to move to places near Islington, rather than to more distant locales. This principle was later explored by Reilly (1931), who developed an explicit specification of distance decay for migration models, and was then applied to trade flows by Isard (1954), flows of information by Gould and White (1985), and now sees extensive application for many different kinds of interaction (Oshan, 2021).
Figure 1. Out-migration from the central London borough of Islington. Darker colors indicate more families have moved from Islington to other boroughs in and around London, showing that people in Islington are more likely to move to closer boroughs than more distant boroughs. Map tiles by Stamen Design, under CC BY 3.0. Data by OpenStreetMap, under ODbL. Source: authors.
In this sense, distance decay refers to interactions that we directly measure and predict to decrease as distance increases. Separation is one predictor of interaction, possibly among many others. Together, this means that distance decay, the existence and strength of a negative relationship between separation and interaction, is a core question in this literature.
As a reflection of this, most studies in this literature all share the same basic traits that stem from their adaptation of (or reaction to) properties of distance decay in physics, which will be discussed in Section 3.1. Specifically, distance decay is usually expected to"exist;" in some sense. If it does not, then the model is assumed to be incorrectly specified, distance in-artfully measured, or parameters incorrectly estimated. Thus, in this spatial interaction modelling perspective, distance decay is a theoretical construct embedded in models that may "hold" to varying degrees.
While spatial interaction models were being formalized, empirical interest in distance decay in similarity was also growing. For example, Stephan (1934), was concerned that most statistical analyses ignored how nearby census tracts tended to have similar sociodemographic characteristics. The chief concern was not about explicit interaction between census tracts, but rather an implicit similarity between tracts that decayed with distance. To measure this, Matheron (1963) developed the variogram, which describes the distance decay in covariation for geographic measurements. In most geographic analyses, co-variation does tend to decrease as separation between measurements increases. However, this is not always the case, and there is often something useful revealed about the process generating the data when distance decay in similarity does not hold (Griffith, 2019). Thus, work using the variogram has become widespread in both social and physical sciences, driven by how useful the variogram (and related tools and concepts) are in describing and controlling for the statistical effects of distance decay in the similarity of measurements.
Thus, "distance decay" as used by geographers refers to one of these two relationships: either similarity implicit in the structure of geographic data (i.e. measured by a variogram) or interactions explicit between geographic entities (i.e. modeled by a spatial interaction model). Thus, these two senses of "distance decay" reflect separate perspectives for how distance decay emerges in geography (Wolf et al., 2020). The following sections discuss these two perspectives in detail, illustrating their fundamental similarities and showing how separation or relation may change, but distance decay will likely remain.
3.1 Distance Decay in Interaction: the Gravity Model
At its core, spatial interaction models seek to predict the interaction between two entities, like trade between countries, migration between regions, or instant messages between friends. The interaction (sometimes also called a "flow" in trade or migration studies) originates somewhere (we'll call this site the origin, i) and ends up somewhere else (the destination, j). This flow is is denoted fij.
Then, interaction models predict the size of each flow using three factors. First, "pull" factors (sometimes called "attractiveness," Aj) encourages agents to interact with a destination j. As a complement, the "push" factors (known also as "propulsiveness," spelled Pj) encourage interaction from an origin. These are generally different for different places, and will be defined differently problem-to-problem depending on the interaction being studied. For example, in studies of migration, a push factor might be an economic collapse or invasion in possible origin countries, while pull factors might be low unemployment or high standards of living in possible destination countries.
Figure 2. Distance decay functions for a gravity model of spatial interaction from Equation 1. Four different values of ß are shown to indicate different "speeds" of distance decay. For a small value of ß = - 0.1, interaction between an origin and a destination decays very slowly they get further apart. For a larger value of ß = -1, interaction decays very quickly. Source: authors.
The next part of the classic interaction model is a measure of distance between i and j, generally spelled dij. Again, this may be a physical distance, or may be measured using a more abstract notion of "separation." We will discuss this in more detail later.
Finally, to assemble the model, we need to weight each of these factors according to how important they are in generating interaction. Unfortunately, the proper values of these weights are unknown, so they have to be estimated from interaction data. Here, we use Greek symbols to stand-in for these unknown values:
reflects an unknown "baseline" level of interaction, 
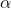adjusts the importance of attractiveness Ak, 
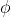adjusts propulsiveness, and 
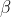reflects the importance of distance to flow. The gravity model of spatial interaction brings these factors together to predict interaction:
All of the unknown values (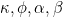
) have to be estimated from the data, and the values of 
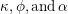will depend on the structure of the push and pull factors. However, a negative estimate of ß is usually obtained from the data, suggesting that interaction between i and j decreases as distance increases. Indeed, a large literature focuses on understanding and adjusting for things that might "confound" distance decay, causing ß estimates to be positive and implying interaction increases with distance. See Oshan (2021) for a detailed discussion. As a result, contemporary analyses of interaction may use more sophisticated models that control for confounding effects (such as accessibility (Fotheringham, 1983)) and yield ß estimates that represent distance decay.
The structure of this decay is quite flexible in practice. Figure 2 shows three values of ß where the expected interaction strength (on the vertical axis) is plotted against the distance between origins and destinations (on the horizontal axis). All interaction fades as separation increases, but interaction decays more quickly as gets more negative. Alternatively, Figure 3 shows how different shapes of distance decay functions will "spread" interaction differently. The standard "power" decay function (used in Eq. 1, for example) will tend to predict that interactions between observations are highly concentrated among the closest pairs, while a linear decay will spread interactions out over more distant pairs.
Figure 3. Three distance decay functions that "spread" interaction differently among observations. The "power" decay function is generally the most concentrated, while linear (or logarithmic forms, not pictured) are the least concentrated. Source: authors.
Unfortunately, deciding how to measure "distance" or what form of "decay" to use can be quite difficult. Theoretical arguments about the form of decay suggest that the importance of distance decreases with the size of the trip (Haggett, 1979). For example, a walk that takes ten minutes will be fairly disrupted by a detour that takes ten extra minutes, but the same detour will matter much less in a three-hour trek. But, this might not be the same in all processes. Therefore, choosing between forms of distance decay is often a data-intensive process where many models are fit with different distance decay functions, and then compared based on their predictive ability.
In addition to the strength and the form of decay, the measurement of separation is also quite important. We have avoided this topic so far because it can be very complex. Note that the detour example above expressed distance in terms of time, not space. Other kinds of distance may not refer to space-time locations at all! Therefore, given its theoretical importance, we dedicate an entire section later to thinking about how to measure "distance" in distance decay, and discuss the social and material forces that are re-shaping distance itself.
3.2 Distance Decay in Similarity: the Variogram
Distance decay is also used in geography to refer to how nearby things tend to be more similar than distant things. This distance decay in similarity is intimately related to the idea of spatial autocorrelation, which applies in a much more general sense than the distance decay we see in interaction. This is because distance decay in similarity is not limited to studies of interaction (like trade, social networks, or migration), and so is frequently used to describe any set of geographic measurements. So, let us consider one of the most common ways of thinking about distance decay in similarity: the variogram.
At its most basic, the variogram measures the similarity between pairs of observations separated by a given distance. Variograms define similarity as the variance of the differences between measurements. It calculates this variance for sets of sites separated by some distance, h. For now, let us assume that we have some number of sites Nh that are separated exactly by h, meaning dij = h. Then, the value of the variogram for distance h, spelled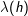
, is defined as the sum of squared differences between pairs of sites i, j that are separated by exactly h:
In this instance, we can compute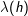
for any separation h, and plot the value of this function as h goes from describing very close measurements to very distant measurements. In practice, we usually compute 
) for pairs of observations separated by approximately h. For example, if h = 2 kilometers, we might use pairs of observations separated by between 1.8 and 2.2 kilometers. This is because there are only a xed number of observation pairs, but infinitely many values of h for which the variogram has to be evaluated. A "best fit" curve is usually estimated to describe the shape of computed values of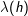 
. As in spatial interaction models, the form of this curve is flexible. Regardless of this form, large values of 
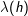indicate that observations separated by distance h are very different, and small values of 
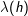indicate that they are very similar. So, the faster the variogram increases, the stronger the distance decay in similarity. Figure 4 shows this for many different "ranges," or separations at which the variogram attains its "stable" long-run value (called the "sill").
Figure 4.Three variograms plotted from simulated data. Three different "ranges" are shown that influence the speed of distance decay. The variogram with fastest distance decay reaches its stable long-run value (the "sill") first. Source: authors.
For variograms (and other related methods), distance decay means that similarity between measurements decreases as separation increases. Because variograms are not limited to studying distance decay in geographic data about interactions, they are widely used and heavily customized. As a consequence, many methods build upon the basic premise of the variogram. For example, spatial correlograms measure similarity using the correlation between pairs of values separated by a given distance. Alternatively, some scholars build variograms for distances in an ordinal sense, computing similarity among some number of nearest neighbors to each measurement. As is the case with gravity models in spatial interaction, variograms are only one part of a broad and flexible framework used throughout geographical analysis.
4. Understanding "Distance" in Distance Decay
In previous sections, we have examined how distance decay is used and analyzed in two different senses. In both cases, distance decay describes how a kind of relationship gets smaller as the separation between things gets larger. However, spatial interaction models think of "relationship" as some kind of interaction that we directly measure, while variograms think of "relationship" as an implicit similarity between measurements. We also discussed how different mathematical forms can change how decay is distributed among pairs of observations.
This leaves one last term undefined: how should we measure "separation"? The previous sections simply referred to a "distance" or "separation," and did not specify how this was to be measured. This section will provide more detail on how separation may (or may not) be usefully defined and measured, as well as discuss how new technological and social developments affect how we conceptualize distance. Most of this discussion refers explicitly to ideas of distance decay in interaction, since these are questions where the presence (or absence) of distance decay is directly under study in a measurement of interaction. However, more abstract notions of distance and the \death of distance" affect studies of distance decay in separation, too.
4.1 Measuring Distance in Space and Time
Our initial definition of distance decay used the term "separation" to indicate that "distance" may need to be defined in very abstract ways for social or economic processes. Put simply, distance decay in a process might not be apparent if you use straight-line (a.k.a. "Euclidean") distance. In a very basic sense, humans live on a curved Earth; straight-line distance distorts this, and it is more accurate to measure distances using paths along the surface of a curved and bumpy planet. But, this is only one way that simple physical ideas of distance fail to capture our complex socially mediated reality. Paths that interactions take from their origins to their destinations are rarely straight, and often involve changes in the mode of travel. For example, a migrant might take a train to an airport, fly north to a layover, and then east to their final destination. Together, this implies a more abstract socially-mediated notion of distance, called travel cost, that reflects how expensive interaction is using some common resource like time or money. Travel cost definitions of separation have long been used to study distance decay (e.g. Harris, 1954), but can be very hard to measure or represent. In urban contexts (for example), some individuals prefer to chose paths that take less time (time costs), are straighter (turn costs), less expensive (monetary costs), more environmentally friendly (climate costs), or involve fewer changes between modes of transit (transfer costs). The considerations that any agent might make is too nebulous to be useful, so travel costs are usually measured using a weighted combination of a limited set of costs.
This method of analysis only gets us so far, however. Travel cost can vary from person to person, and individuals might strongly disagree about the "cost" of a route because they weight costs differently from one another. Costs may depend on the context in which actors make decisions (Eldridge and Jones III, 1991; Fotheringham, 1983). This means that the structure of travel costs can change within a system, or distance decay itself can behave differently depending on where in the system it is studied. Travel costs can also change over time, as individuals' judgments evolve or systems of transport are transformed. Thus, while a physical distance between two places may be fairly consistent, the relevant socially-mediated travel costs can and do vary widely between people, places, and times.
4.2 Beyond Space and Time Distance Decay
Going further, distance decay can even apply in situations where neither physical nor travel distance matters. Instead, behavioral or social measures of relation may be important when understanding how people move through their city or select where they want to live. Foundational work in geography shows that individuals perceive space in ways that may not map very well to physical or travel definitions of separation (Gould and White, 1985; Golledge and Hubert, 1982). For example, people may think of familiar or more desirable destinations as "closer," regardless of travel cost or distance. This more subjective notion of separation undoubtedly affects the way individuals reason about interaction, and thus affects how distance decay works in practice.
Alternatively, social or economic similarity itself can act as a separation over which distance decay acts (Gatrell, 1983). As an example, the idea of homophily in sociology describes how contact between similar people is more common than contact between dissimilar people (McPherson et al., 2001). Here, distance is defined as a social separation reflecting the demographic or psychological dissimilarity between people. In this case, as social separation between people increases, their interactions decrease - a social distance decay.
This removes the idea of distance decay from space and time entirely. As in our discussion of the two most common definitions of "relation," decisions about how to define "distance" or "relation" will determine how distance decay is made meaningful in a given study. This, in turn, structures any inquiry into distance decay itself. Therefore, it is important to critically articulate and defend the mechanism (or mechanisms) by which separation affects the relationships under study, and then measure separation and relation as accurately as possible.
4.3 The Present and Future Transformations of Distance Decay
As a consequence of the socially-mediated (and at times deeply personal) nature of separation, the way that distance "works" has changed substantially over time. This has been well-studied in historical work on economic geography and the urban system (Borchert, 1967). The continued relevance of distance (and, as a consequence, the existence of distance decay) is seriously debated today.
Some have speculated that physical distance is becoming less important because of the rise of online interaction (Cairncross, 2001). An instant message is approximately instant, whether you talk to your next-door neighbor or someone on the other side of the world. As a behavioral example, Lendle et al. (2016) shows that the internet supplants consumers' local knowledge networks. This decreases the importance of nearby people and/or marketplaces in learning about products and thus weakens distance decay in consumer interactions with sellers. Thus, the power of distance decay may weaken in consumer decision-making.
Ultimately, however, distance decay remains strong in many social processes. The death of distance (decay) in studies of urban transit systems may be less radical than anticipated (Rietveld and Vickerman, 2004). For studies in trade, Buch et al. (2004) discusses the "distance puzzle": even as transportation costs have been slashed dramatically (in part due to digital technologies), estimates of the strength of distance decay in trade remain stable. Buch et al. (2004) finds that this is because spatial interaction models estimate distance decay as a relative propensity for "near" things to interact more than "distant" things, not as an absolute determinant of interaction. Distant trade partners still pay more transit costs than near trade partners even though everyone pays less overall. Thus, despite the "death of distance," distance decay still exists.
Another contemporary debate about distance decay focuses on the COVID-19 pandemic. Because of "stay at home" orders and the attendant rise in remote working, some believe we are seeing structural changes in workforce composition may accelerate the "death of distance." However, there are good conceptual reasons to believe that distance decay will remain important in peoples' location and consumption decisions (Reades and Crookston, 2021). Indeed, as the internet increasingly mediates human interaction, distance decay is still quite strong according to digitally-relevant notions of separation (Couclelis, 1996; Tranos and Nijkamp, 2013). Distance decay may increase in relevance for human geography, but with digitally- or socially-mediated distances playing an increasingly important role. However, these structural changes in the geographic patterns of work and residence are still evolving rapidly as the COVID-19 pandemic evolves, so the ultimate effect of these changes remain unclear (Rose-Redwood et al., 2020).
5. Conclusion
Distance decay is a fundamental concept in geography. At its core, distance decay describes how the relationships between entities get weaker as separation increases; nearer things will tend to be more related than distant things. In practice, this applies both to cases where we see the relationships directly (like trade or migration), and cases where the relationships are only indirectly measured. We discuss how the gravity model of spatial interaction and the variogram represent these two cases, respectively. Both senses of distance decay are important to understand, as either (or both) are present in many processes. We discuss how the idea of "distance" may be more than physical, reflecting socially-mediated travel costs, individual perceptions of distance, or socioeconomic similarity. In addition to being one of the oldest concepts in geographic analysis, distance decay will remain relevant even as new technologies and world events transform how distance is experienced.
Borchert, J. R. (1967). American Metropolitan Evolution. Geographical Review, 57(3):301. doi: 10.2307/212637.
Buch, C. M., JKleinert, J., and Toubal, F. (2004). The distance puzzle: on the interpretation of the distance coefficient in gravity equations. Economics Letters, 83(3):293-298. doi: 10.1016/j.econlet.2003.10.022.
Cairncross, F. (2001). The Death of Distance: How the Communications Revolution Is Changing Our Lives. Harvard Business School Press, Boston.
Couclelis, H. (1996). The Death of Distance. Environment and Planning B: Planning and Design, 23(4):387-389, August 1996. doi: 10.1068/b230387.
Eldridge, J. D. and Jones III, J. P. (1991). Warped Space: A Geography of Distance Decay. The Professional Geographer, 43(4):500-511. doi: 10.1111/j.0033-0124.1991.00500.x.
Fotheringham, A. S. (1983). A New Set of Spatial-Interaction Models: The Theory of Competing Destinations. Environment and Planning A: Economy and Space, 15:15-36.
Gatrell, A. C. (1983). Distance and space: a geographical perspective. Oxford University Press, USA.
Golledge, R. G., and L J Hubert, L. J. (1982). Some Comments on Non-Euclidean Mental Maps. Environment and Planning A: Economy and Space, 14(1):107-118. doi:10.1068/a140107.
Gould, P. and White, R. (1985). Mental Maps. Penguin Books, Hoboken.
Griffith, D. A. (2019). Negative Spatial Autocorrelation: One of the Most Neglected Concepts in Spatial Statistics. Stats, 2(3):388-415. doi: 10.3390/stats2030027. https://www.mdpi.com/2571-905X/2/3/27.
Grigg, D. B. (1977). E.G. Ravenstein and the "laws" of migration. Journal of Historical Geography, 3:41-54,1977.
Haggett, P. (1979). Geography: a modern synthesis. Harper & Row series in geography. Harper and Row, New York ; London, 3rd ed. edition.
Harris, C. D. (1954). The Market as a Factor in the Localization of Industry in the United States. Annals of the Association of American Geographers, 44(4):315-348. doi: 10.2307/2561395.
Isard, W.. Location theory and trade theory: Short-run analysis. Quarterly Journal of Economics, 68:305-320, 1954.
Lendle, A., Olarreaga, M., Schropp, S., and Vezina, P-L. (2016). There Goes Gravity: eBay and the Death of Distance. The Economic Journal, 126(591):406-441. doi: 10.1111/ecoj.12286.
Matheron, G. (1963). Principles of geostatistics. Economic Geology, 58:1246-1266.
McPherson, M., Smith-Lovin, L., and Cook, J. M. (2001). Birds of a Feather: Homophily in Social Networks. Annual Review of Sociology, 27(1):415-444.
Oshan, T. M. (2021). The spatial structure debate in spatial interaction modeling: 50 years on. Progress in Human Geography, 45(5):925-950. doi: 10.1177/0309132520968134.
Ravenstein, E. G. (1885). The laws of migration. Journal of the Statistical Society of London, 48:167-235.
Reades, J. and Crookston, M. (2021). Why Face-to-Face Still Matters: The Persistent Power of Cities in the Post-Pandemic Era. Policy Press. Google-Books-ID: YI8kEAAAQBAJ.
Reilly, W. J. (1931). The law of retail gravitation. Knickerbocker Press.
Rietveld, P. and Roger Vickerman. (2004). Transport in regional science: The "death of distance" is premature*. Papers in Regional Science, 83(1):229-248, 2004. doi: 10.1007/s10110-003-0184-9.
Rose-Redwood, R., Rob Kitchin, Elia Apostolopoulou, Lauren Rickards, Tyler Blackman, Jeremy Crampton, Ugo Rossi, and Michelle Buckley. (2020). Geographies of the COVID-19 pandemic. Dialogues in Human Geography, 10(2):97-106.. doi: 10.1177/2043820620936050.
Stephan, F. F. (1934). Sampling Errors and Interpretations of Social Data Ordered in Time and Space. Journal of the American Statistical Association, 29(185A):165-166. doi: 10.1080/01621459.1934.10506245.
Tobler, W. R. (1995). Migration: Ravenstein, Thornthwaite, and beyond. Urban Geography, 16:327-343. doi: 10.2747/0272-3638.16.4.327.
Tranos. E. and Nijkamp. P. (2013). The Death of Distance Revisited: Cyber-Place, Physical and Relational Proximities. Journal of Regional Science, 53(5):855-873. doi: 10.1111/jors.12021.
Wolf, L. J., Sean Fox, Rich Harris, Ron Johnston, Kelvyn Jones, David Manley, Emmanouil Tranos, and Wenfei Winnie Wang. (2020). Quantitative geography III: Future challenges and challenging futures. Progress in Human Geography, page 0309132520924722 . doi: 10.1177/0309132520924722.
Keywords: