AM-17 - Intervisibility

- Define “intervisibility”
- Outline an algorithm to determine the viewshed (area visible) from specific locations on surfaces specified by DEMs
- Perform siting analyses using specified visibility, slope, and other surface related constraints
- Explain the sources and impact of errors that affect intervisibility analyses

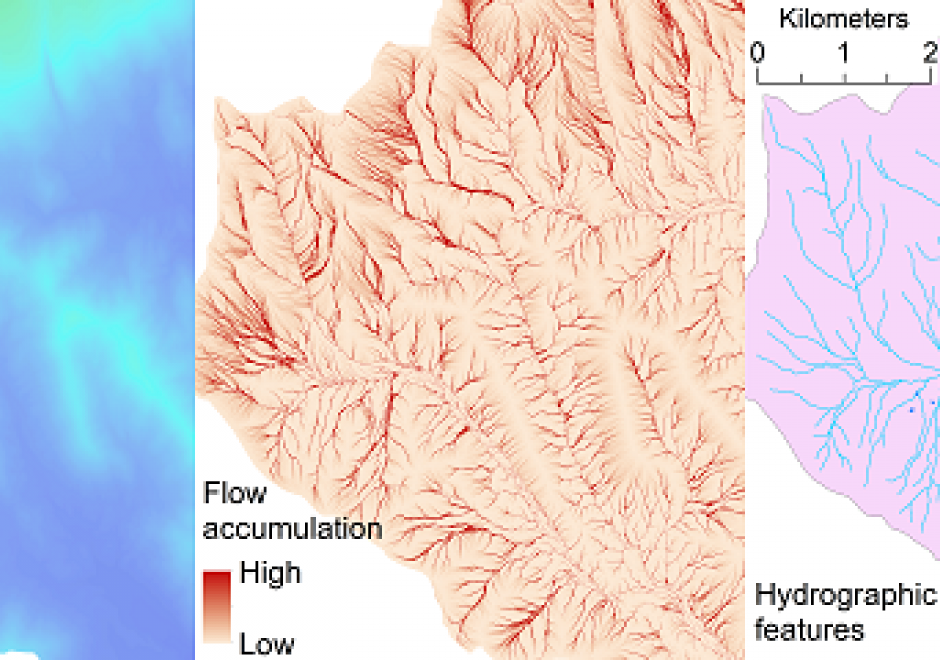

AM-66 - Watersheds and Drainage Networks
This topic is an overview of basic concepts about how the distribution of water on the Earth, with specific regard to watersheds, stream and river networks, and waterbodies are represented by geographic data. The flowing and non-flowing bodies of water on the earth’s surface vary in extent largely due to seasonal and annual changes in climate and precipitation. Consequently, modeling the detailed representation of surface water using geographic information is important. The area of land that collects surface runoff and other flowing water and drains to a common outlet location defines a watershed. Terrain and surface features can be naturally divided into watersheds of various sizes. Drainage networks are important data structures for modeling the distribution and movement of surface water over the terrain. Numerous tools and methods exist to extract drainage networks and watersheds from digital elevation models (DEMs). The cartographic representations of surface water are referred to as hydrographic features and consist of a snapshot at a specific time. Hydrographic features can be assigned general feature types, such as lake, pond, river, and ocean. Hydrographic features can be stored, maintained, and distributed for use through vector geospatial databases, such as the National Hydrography Dataset (NHD) for the United States.