AM-10 - Spatial Interaction
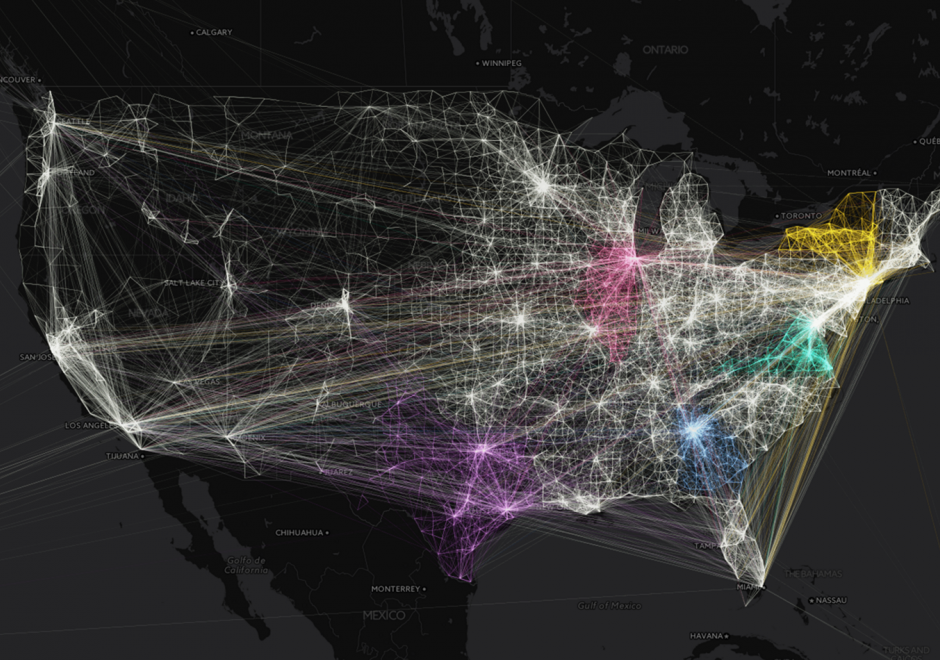
Spatial interaction (SI) is a fundamental concept in the GIScience literature, and may be defined in numerous ways. SI often describes the "flow" of individuals, commodities, capital, and information over (geographic) space resulting from a decision process. Alternatively, SI is sometimes used to refer to the influence of spatial proximity of places on the intensity of relations between those places. SI modeling as a separate research endeavor developed out of a need to mathematically model and understand the underlying determinants of these flows/influences. Proponents of SI modeling include economic geographers, regional scientists, and regional planners, as well as climate scientists, physicists, animal ecologists, and even some biophysical/environmental researchers. Originally developed from theories of interacting particles and gravitational forces in physics, SI modeling has developed through a series of refinements in terms of functional form, conceptual representations of distances, as well as a range of analytically rigorous technical improvements.


AM-13 - Multi-criteria evaluation