AM-03 - Buffers
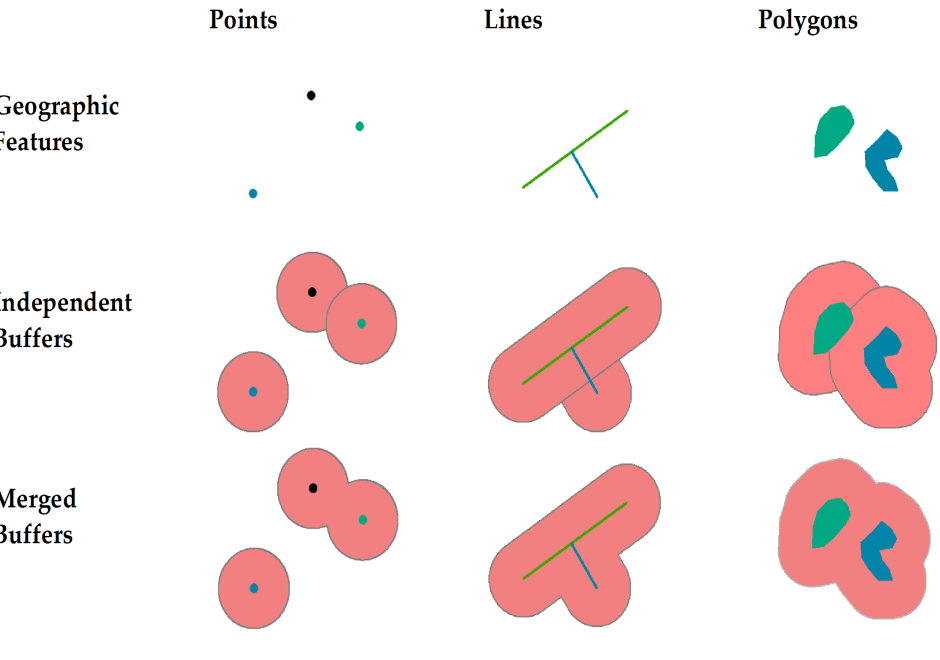
This short article introduces the definition of buffer and explains how buffers are created for single or multiple geographic features of different geometric types. It also discusses how buffers are generated differently in vector and raster data models and based on the concept of cost.

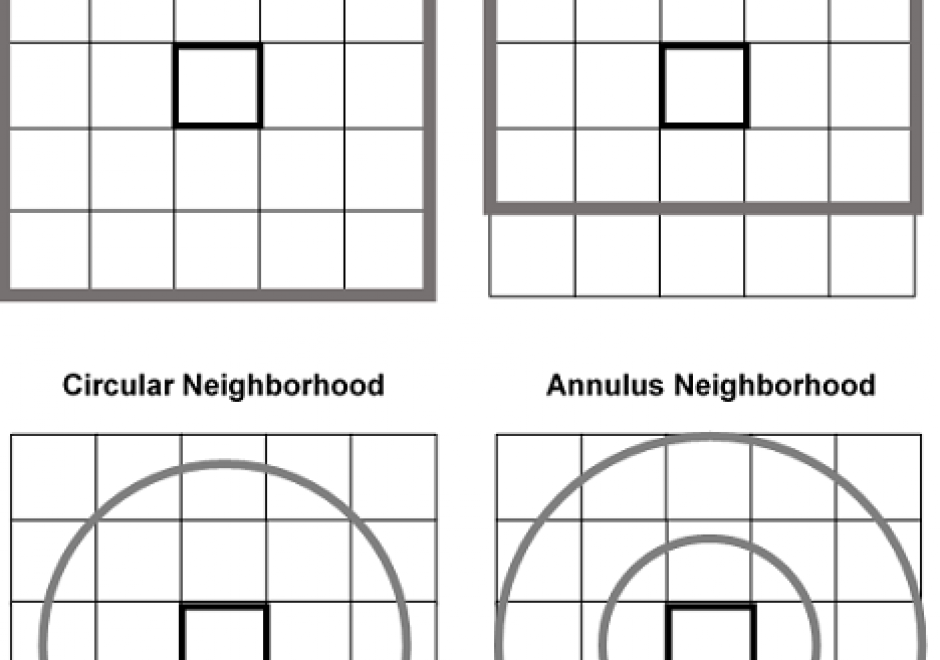
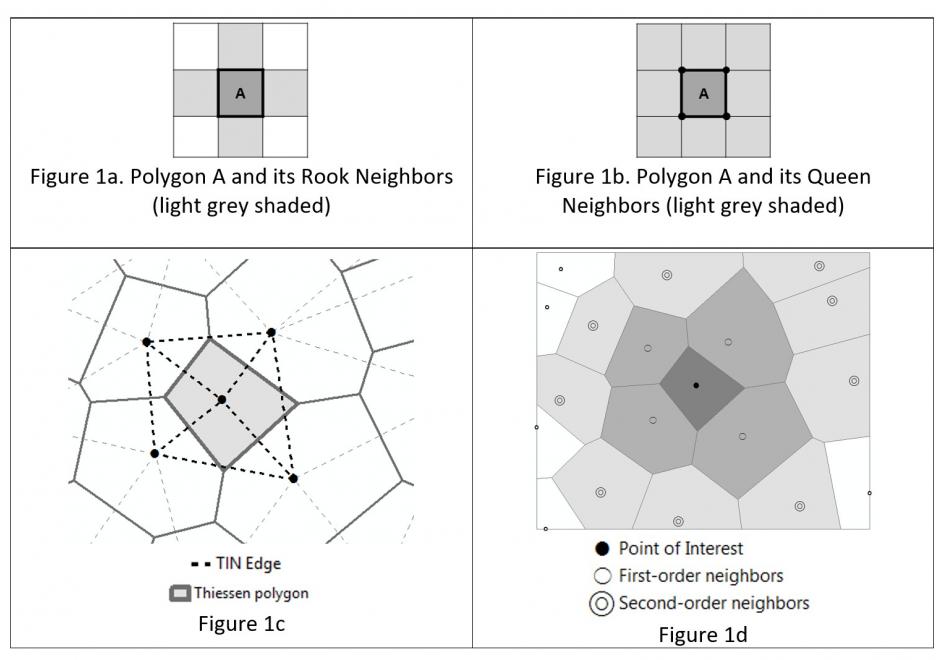
FC-40 - Neighborhoods
Neighborhoods mean different things in varied contexts like computational geometry, administration and planning, as well as urban geography and other fields. Among the multiple contexts, computational geometry takes the most abstract and data-oriented approach: polygon neighborhoods refer to polygons sharing a boundary or a point, and point neighborhoods are defined by connected Thiessen polygons or other more complicated algorithms. Neighborhoods in some regions can be a practical and clearly delineated administration or planning units. In urban geography and some related social sciences, the terms neighborhood and community have been used interchangeably on many occasions, and neighborhoods can be a fuzzy and general concept with no clear boundaries such that they cannot be easily or consensually defined. Neighborhood effects have a series of unique meanings and several delineation methods are commonly used to define social and environmental effects in health applications.