FC-22 - Geometric Primitives and Algorithms
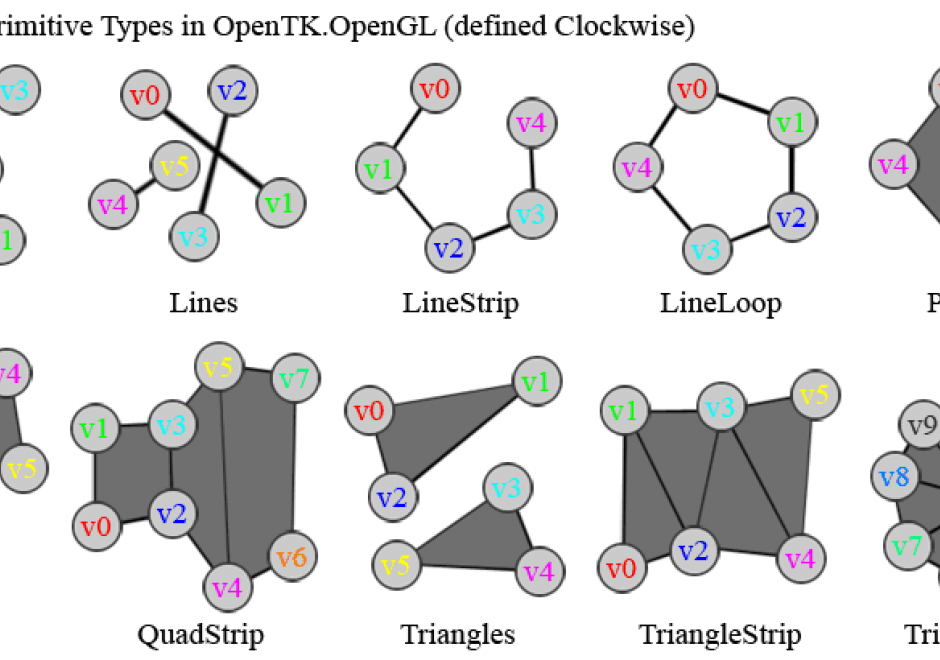
Geometric primitives are the representations used and computations performed in a GIS that concern the spatial aspects of the data, data objects described by coordinates. In vector geometry, we distinguish in zero-, one-, two-, and three-dimensional objects, better known as points, linear features, areal or planar features, and volumetric features. A GIS stores and performs computations on all of these. Often, planar features form a collective known as a (spatial) subdivision. Computations on geometric objects show up in data simplification, neighborhood analysis, spatial clustering, spatial interpolation, automated text placement, segmentation of trajectories, map matching, and many other tasks. They should be contrasted with computations on attributes or networks.
There are various kinds of vector data models for subdivisions. The classical ones are known as spaghetti and pizza models, but nowadays it is recognized that topological data models are the representation of choice. We overview these models briefly.
Computations range from simple to highly complex: deciding whether a point lies in a rectangle needs four comparisons, whereas performing map overlay on two subdivisions requires advanced knowledge of algorithm design. We introduce map overlay, Voronoi diagrams, and Delaunay triangulations and mention algorithmic approaches to compute them.

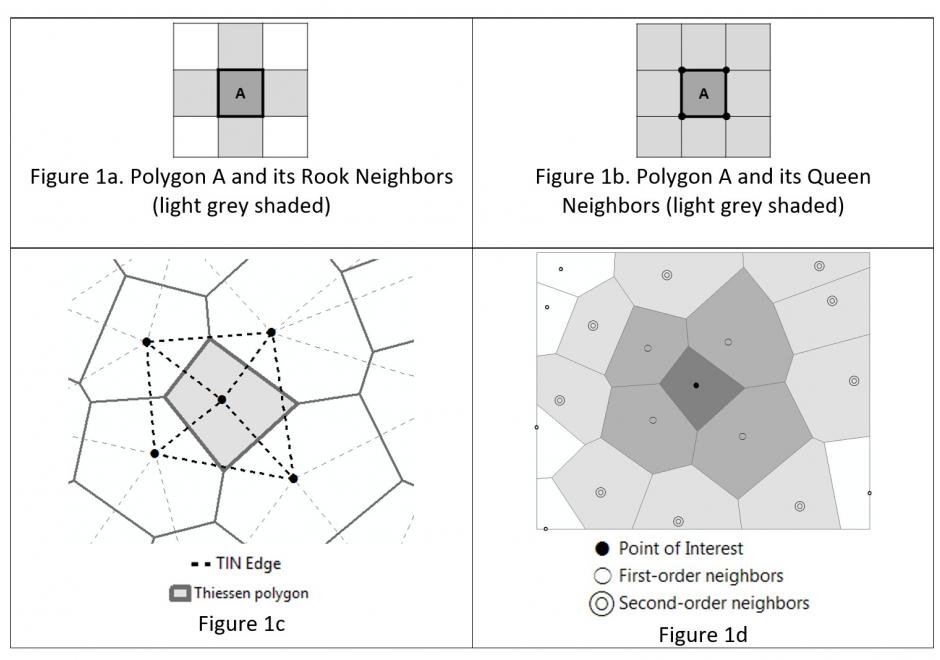
FC-40 - Neighborhoods
Neighborhoods mean different things in varied contexts like computational geometry, administration and planning, as well as urban geography and other fields. Among the multiple contexts, computational geometry takes the most abstract and data-oriented approach: polygon neighborhoods refer to polygons sharing a boundary or a point, and point neighborhoods are defined by connected Thiessen polygons or other more complicated algorithms. Neighborhoods in some regions can be a practical and clearly delineated administration or planning units. In urban geography and some related social sciences, the terms neighborhood and community have been used interchangeably on many occasions, and neighborhoods can be a fuzzy and general concept with no clear boundaries such that they cannot be easily or consensually defined. Neighborhood effects have a series of unique meanings and several delineation methods are commonly used to define social and environmental effects in health applications.