FC-17 - Proximity and Distance Decay
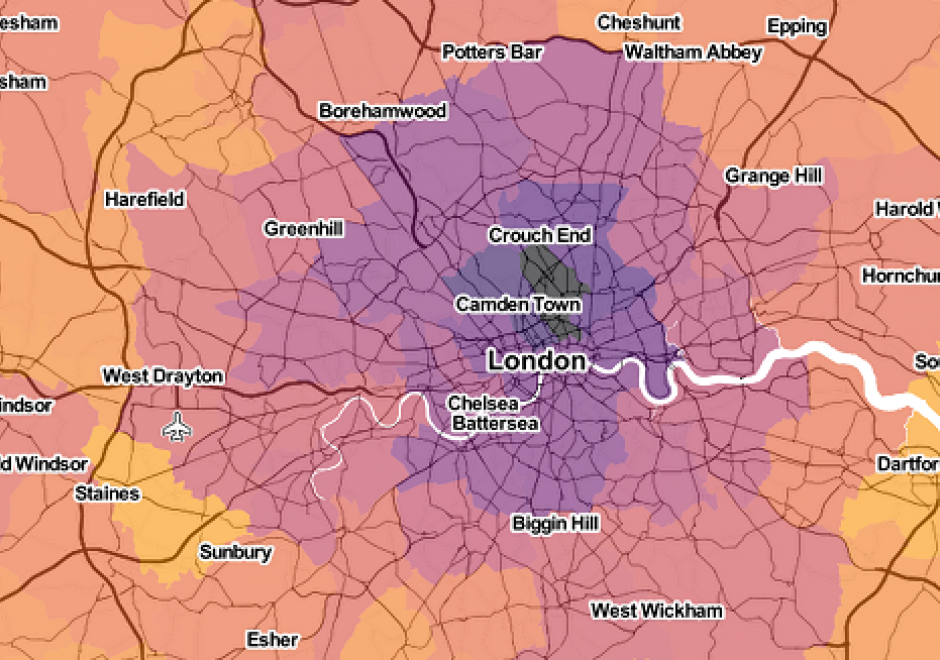
Distance decay is an essential concept in geography. At its core, distance decay describes how the relationship between two entities generally gets weaker as the separation between them increases. Inspired by long-standing ideas in physics, the concept of distance decay is used by geographers to analyze two kinds of relationships. First, the term expresses how measured interactions (such as trade volume or migration flow) generally decrease as the separation between entities increases, as is analyzed by spatial interaction models. Second, the term is used to describe how the implicit similarity between observations changes with separation, as measured by variograms. For either type of relationship, we discuss how "separation" must be clearly articulated according to the mechanism of the relationship under study. In doing this, we suggest that separation need not refer to positions in space or time, but can involve social or behavioral perceptions of separation, too. To close, we present how the "death of distance" is transforming distance decay in uneven ways.



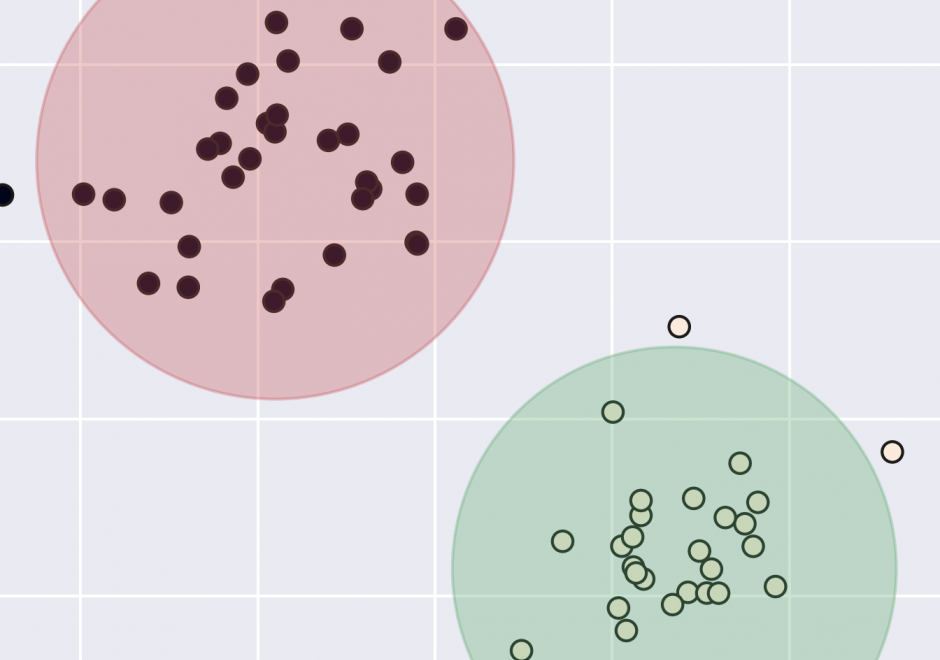
FC-37 - Spatial Autocorrelation
The scientific term spatial autocorrelation describes Tobler’s first law of geography: everything is related to everything else, but nearby things are more related than distant things. Spatial autocorrelation has a:
Positive spatial autocorrelation constitutes the focal point of its past and present; one expectation is that negative spatial autocorrelation will become a focal point of its future.