FC-19 - Networks
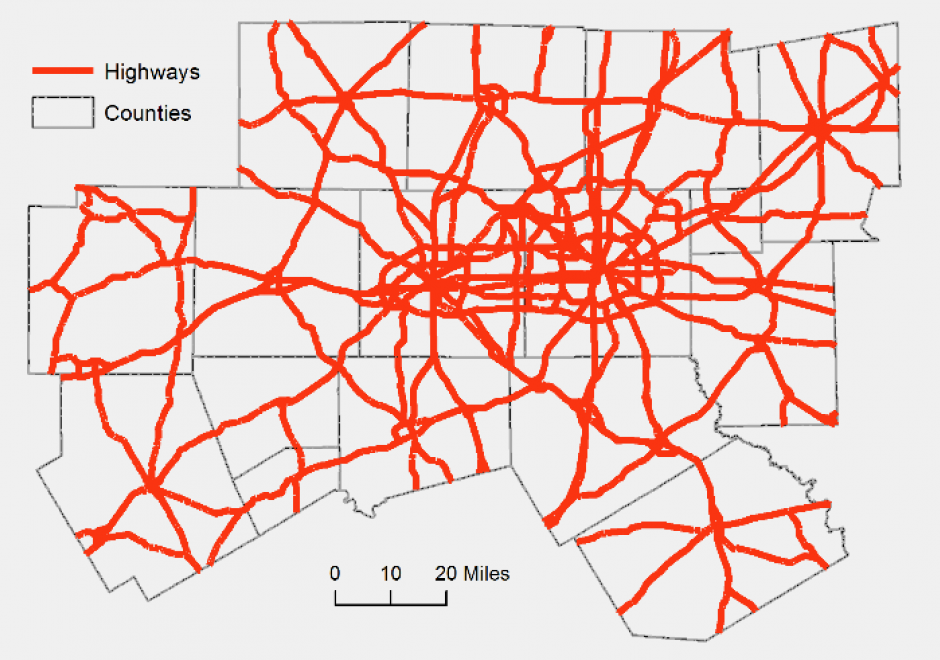
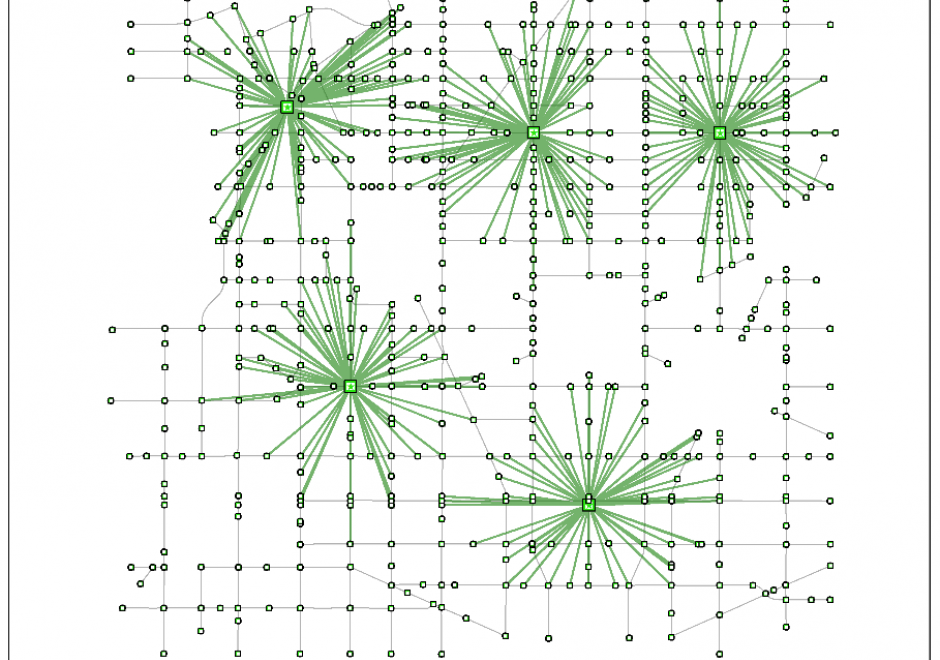
A network is a widely used term with different definitions and methodologies depending on the applications. In GIS, a network refers to an arrangement of elements (i.e., nodes, links) and information on their connections and interactions. There are two types of networks: physical and logical. While a physical network has tangible objects (e.g., road segments), a logical network represents logical connections among nodes and links. A network can be represented with a mathematical notion called graph theory. Different network components are utilized to describe characteristics of a network including loops, walks, paths, circuits, and parallel edges. Network data are commonly organized in a vector format with network topology, specifically connectivity among nodes and links, whereas raster data can be also utilized for a least-cost problem over continuous space. Network data is utilized in a wide range of network analyses, including the classic shortest path problem.



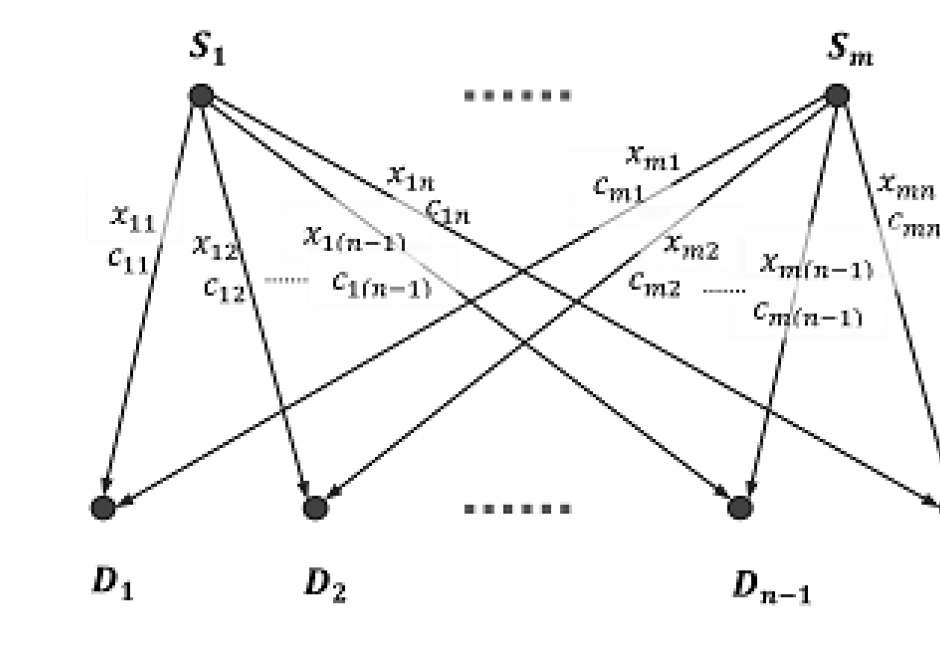
PD-01 - Linear Programming and GIS
Linear programming is a set of methods for finding optimal solutions to mathematical models composed of a set of linear functions. Many spatial location problems can be structured as linear programs. However, even modest-sized problem instances can be very difficult to solve due to the combinatorial complexity of the problems and the associated computational expense that they incur. Geographic Information Systems software does not typically incorporate formal linear programming functionality, and instead commonly uses heuristic solution procedures to generate near-optimal solutions quickly. There is growing interest in integrating the spatial analytic tools incorporated in Geographic Information Systems with the solution power of linear programming software to generate guaranteed optimal solutions to spatial location problems.