CV-18 - Representing Uncertainty
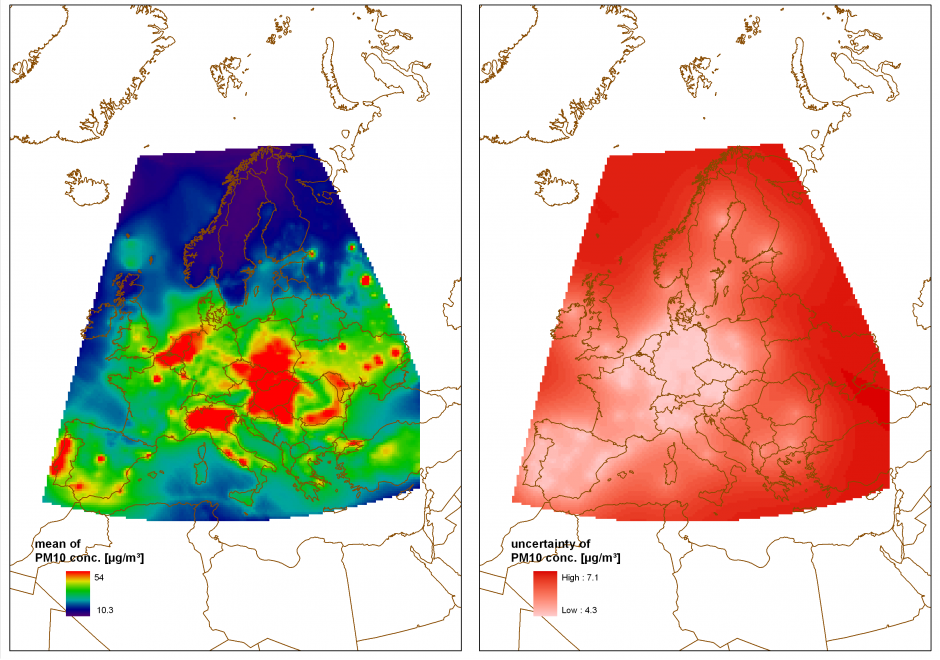
Using geospatial data involves numerous uncertainties stemming from various sources such as inaccurate or erroneous measurements, inherent ambiguity of the described phenomena, or subjectivity of human interpretation. If the uncertain nature of the data is not represented, ill-informed interpretations and decisions can be the consequence. Accordingly, there has been significant research activity describing and visualizing uncertainty in data rather than ignoring it. Multiple typologies have been proposed to identify and quantify relevant types of uncertainty and a multitude of techniques to visualize uncertainty have been developed. However, the use of such techniques in practice is still rare because standardized methods and guidelines are few and largely untested. This contribution provides an introduction to the conceptualization and representation of uncertainty in geospatial data, focusing on strategies for the selection of suitable representation and visualization techniques.






FC-21 - Resolution
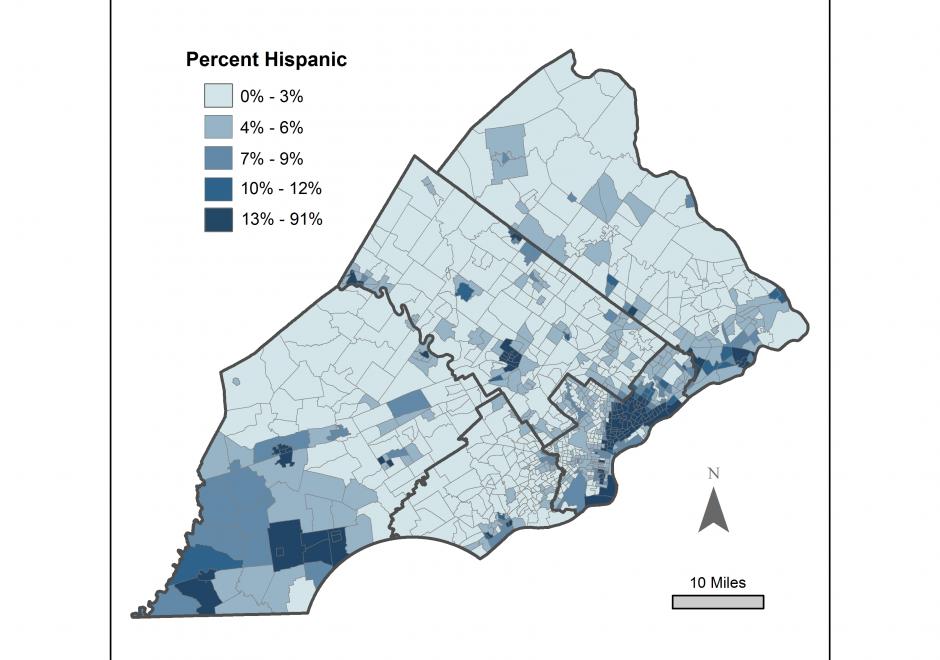
Resolution in the spatial domain refers to the size of the smallest measurement unit observed or recorded for an object, such as pixels in a remote sensing image or line segments used to record a curve. Resolution, also called the measurement scale, is considered one of the four major dimensions of scale, along with the operational scale, observational scale, and cartographic scale. Like the broader concept of scale, resolution is a fundamental consideration in GIScience because it affects the reliability of a study and contributes to the uncertainties of the findings and conclusions. While resolution effects may never be eliminated, techniques such as fractals could be used to reveal the multi-resolution property of a phenomenon and help guide the selection of resolution level for a study.