You are currently viewing an archived version of Topic Shape.
If updates or revisions have been published you can find them at Shape.
Shape is important in GI Science because the shape of a geographical entity can have far-reaching effects on significant characteristics of that entity. In geography we are mainly concerned with two-dimensional shapes such as the outlines of islands, lakes, and administrative areas, but three-dimensional shapes may become important, for example in the treatment of landforms. Since the attribute of shape has infinitely many degrees of freedom, there can be no single numerical measure such that closely similar shapes are assigned close numerical values. Therefore different shape descriptors have been proposed for different purposes. Although it is generally desirable for a shape descriptor to be scale invariant and rotation invariant, not all proposed descriptors satisfy both these requirements. Some methods by which a shape is described using a single number are described, followed by a discussion of moment-based approaches. It is often useful to represent a complex shape by means of a surrogate shape of simpler form which facilitates storage, manipulation, and comparison between shapes; some examples of commonly used shape surrogates are presented. Another important task is to compare different shapes to determine how similar they are. The article concludes with a discussion of a number of such measures of similarity.
Author and Citation Info:
Galton, A. (2017). Shape. The Geographic Information Science & Technology Body of Knowledge (4th Quarter 2017 Edition), John P. Wilson (ed.). DOI: 10.22224/gistbok/2017.4.8.
This version was published on November 16, 2017.
This Topic is also available in the following editions: DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Shape. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital)
Shape is important in GI Science because the shape of a geographical entity can have far-reaching effects on significant characteristics of that entity. Compare, for example, a long thin island with a roughly circular one. In the former a much greater proportion of the land area will be close to the coast, and the major communication links will tend to be parallel to the long axis. These factors may have an impact on vegetation, settlement patterns, trading relations, and much else. In general the shapes of geographical regions are relevant when we consider such things as urban form, trade areas, political units, drainage basins, and habitats. The problem for GI Science is how to characterize the shapes of geographical entities in ways that usefully capture such implications and are amenable to digital manipulation.
In the first instance we should distinguish between physical and mathematical shape. In fact, as discussed in Galton (2013), physical shape is not well defined because "same measurable shape as" is not an equivalence relation on physical entities, in contrast to "same mathematical shape as," which is an equivalence relation on mathematically defined entities. Here we take shape in GI Science to refer to the well-defined mathematical shapes of digital representations of real physical entities, e.g., of the polygons used to represent areal objects in GIS. The use of polygons is justified by the fact that one can approximate any shape arbitrarily closely by using a polygon with sufficiently many vertices (see, e.g., Bunge 1966, who shows further that a shape can be approximated arbitrarily closely by means of equilateral polygons).
In the geographical world we are mainly concerned with two-dimensional shapes such as the outlines of islands, lakes, and administrative areas. But three-dimensional shapes may become important in a discussion of landforms, or when working at a large scale where the vertical dimension of buildings may become important. In this article we shall confine ourselves to a discussion of shape in two dimensions, although many of the ideas we discuss will readily generalize from the two-dimensional case to the three-dimensional (e.g., replacing polygons by polyhedra).
A key feature of shape as an attribute is that it has infinitely many degrees of freedom. This implies that there can be no single numerical measure such that closely similar shapes are assigned close numerical values. As stated by Frolov (1974), "[i]t is obviously fruitless to search for a single universal shape index." One way round this is to use a vector of distinct shape indices, analogous to the use of (red,green,blue) or (hue,saturation,lightness) for representing colour-spaces, which are also intrinsically multi-dimensional. Frolov specifically proposed compactness, dissection, and indentation for this, claiming them to be independent (hence orthogonal) measures.
It is generally - but not always - regarded as desirable for a shape descriptor to be scale invariant and rotation invariant. However, some proposed descriptors fail one or both of these tests. If A is the area of a shape and P its perimeter, then a measure of the form is not scale-invariant, whereas measures such as or are. In the following, we use and to indicate whether a measure is rotation invariant or scale invariant respectively.
Although rotation invariance is generally a desirable characteristic for a shape descriptor, it is worth noting that this is not always considered to be the case. Identically shaped islands, for example, may present different characteristics depending on the orientations of their long axes relative to the prevailing winds or local current flows (and indeed these flows will themselves be differently affected by the differently oriented islands). Arguably, though, the difference in this case has only to do with orientation, and therefore should not be considered an effect of shape as such.
Table 1. The values of some numerical shape descriptors for a selection of simple shapes, illustrating presence or absence of scale and rotation invariance.
2.1 Numerical shape descriptors
Here we cover methods by which a shape is described using a single number; as noted above, combinations of such measures can be used to provide more discriminating vectorial descriptors. Many such methods have been proposed. For some of these, e.g., elongation, rectangularity, and compactness, a number of alternative definitions have been proposed, often involving a higher degree of mathematical sophistication in order to overcome the shortcomings of the naïve definitions. The values of the first six measures listed here are tabulated for some simple figures in Table 1, illustrating in particular how scale- and rotation-invariance apply to some measures but not to others.
1. Area:
2. Perimeter:
3. Area / Perimeter:
4. Area / Perimeter2: . This has range , taking the value only for a circle. It is customary to scale up to (0, 1], using the measure .
5. Aspect ratio. There are two possibilities here:
(a) , i.e., the height/width ratio for the minimum axis-aligned bounding rectangle (-R, +S). This ranges over .
(b) , where dmin and dmax are respectively the shorter and longer dimensions of the absolute (i.e., ot necessarily axis-aligned) minimum bounding rectangle (MBR), which is defined as the least-area rectangle, of any orientation, wholly covering the shape. This measure ranges over (0,1] , with 1 for shapes whose absolute MBR is a square. This measure is called elongatedness by Sonka et al. (1999).
6. Elongation: , where i1 and i2 are the second moments of the shape about its principle axes. (For the meaning of "moments" see section 2.2.)
7. Compactness: This term has been used to describe many different measures. MacEachren (1985) systematically compares 11 proposed measures for compactness and evaluates them with respect to how well they correlate with homogeneity of superposed distributions. The "winning" measure is , where and are the variances of the x and y coordinates of the points within the shape (+R, +S). Further measures of compactness are discussed by Li et al. (2013), who also introduce their own moment-based approach.
8. Eccentricity (Sonka et al. 1999) is the ratio of the maximum chord A to the longest chord B that is perpendicular to A (+R, +S). These do not necessarily agree with the sides of the absolute MBR, so although it is closely related to it, eccentricity is not the same as aspect ratio.
9. Rectangularity (Sonka et al. 1999) is the ratio of the shape's area to that of its absolute MBR. This has values in the range (0,1], with 1 attained when the shape is a rectangle (+R, +S).
2.2 Moment-based approaches
In a binary image, for a shape S whose centroid is located at the origin, the (p,q)th moment (where ) is the integral:
.
Here S(x, y) is understood to be a function which takes the value 1 for points belonging to the shape, and 0 otherwise; this can be generalised to shapes with "fuzzy" membership, using 0 < S (x, y) < 1.
For digital images, which are discrete and finite, the integral can be replaced for computational purposes by the sum:
.
The nth-order moments are those in the set {}.
A complete set of moments of all orders characterizes the shape uniquely; this is an infinite set, reflecting the infinitely many degrees of freedom mentioned above. The low-order moments provide important global information about the shape, whereas the higher-order moments increasingly reflect fine details. For the purpose of quantifying the most salient features for applications such as shape recognition or approximation, just the lower order moments suffice:
1. The zeroth order moment of a binary shape is just its area.
2. The first-order moments and are zero for a shape centered at the origin, but for other shapes they indicate the position of the centroid.
3. The second-order moments can be used to compute the "image ellipse," that is an "inertially equivalent" elliptical approximation to the shape, and also the principal axes of the shape and its radii of gyration.
4. The third-order moments allow computation of the skewness of the shape, that is, its degree of deviation from symmetry about the centroid (for its projections on the coordinate axes).
5. The fourth-order moments give the kurtosis of the image projections, that is the "peakedness" of the projection.
For further details, see Hu (1962), Teague (1980), and Prokop & Reeves (1992).
For many purposes it is convenient to represent a complex shape by means of a "surrogate" shape of simpler form which facilitates storage, manipulation, and comparison between shapes. A generally desirable property of such surrogates is ease of computation. The properties of rotation invariance and scale invariance must be interpreted somewhat differently here: rotation invariance now means that as a shape is rotated, its surrogate rotates with it, by the same amount, while remaining congruent; and scale invariance means that as a shape is enlarged, its surrogate is also enlarged, by the same amount. Examples of commonly used shape surrogates are:
1. Minimum bounding rectangle. As noted above, this comes in two forms, axis-aligned (-R, +S) and absolute (+R,+S).
2. Convex Hull (+R, +S). This is the smallest convex shape containing the given shape. It has well-researched mathematical and computational properties.
3. Various "non-convex" hulls (usually +R, +S). These are designed to capture details that may be missed by the convex hull, such as the presence of large "bays" in the outline of a region, while still preserving tractable computational characteristics. Examples include the alpha-hull (Edelsbrunner 1983) and chi-hull (Duckham et al., 2008).
4. Quadtrees (-R, +S). The shape is inscribed in a square, which is divided into four quadrants. Each quadrant which includes part of the shape is marked "1," the remainder "0." The same procedure is recursively applied to each square marked with a "1" as many times as desired. This results in a compact tree structure, or "quadtree," from which the shape can be recovered at a level of detail corresponding to the depth of the recursion. The analogous construction in three dimensions is called an "octree."
5. Skeletons (+R,+S). A skeleton is a representation of a two-dimensional shape as a network of interior lines. A typical example, the topological skeleton, or medial axis, is the locus of centers of circles inscribed within the shape and tangent to it in two or more places. Figure 1 shows a shape and its medial axis together with a selection of the circles whose centers define it.
6. Image ellipse (+R,+S), as described above in the section on moment-based approaches.
This list is far from exhaustive, and researchers regularly come up with novel shape surrogates for different purposes - see for example Zhang & Atkinson (2016).
Figure 1. A shape with its medial axis and some of the circles whose centers define it.
Some of these shape surrogates can be applied not only to connected regions but also to the "virtual shapes" formed by patterns of disconnected point-like entities. Indeed, in the case of non-convex hulls, this is the primary application. Roughly speaking, this can be described as assigning a shape to the wood, given the positions of the trees.
It is often required to compare different shapes to determine how similar they are. This can be used in image retrieval, where, for example, one might search for images of boats from an image collection by looking for shapes that are sufficiently similar to one of a set of "standard" boat images in a reference collection. In geography one can investigate how far similarly-shaped regions are similar in other respects as well, thereby determining which characteristics of regions are influenced by their shapes.
One way of measuring similarity is simply to take any of the numerical shape descriptors described above and compare its values for the shapes being compared. Another method is to take some measure of distance between regions and superpose the two shapes so that this distance is minimized. This gives a measure of difference rather than similarity. Examples of such distance measures are:
1. Hausdorff distance between two regions is the largest distance between any point in either one of the regions and the nearest point in the other; here the shapes are assumed to include their own boundary points, so that "largest" and "nearest" are well-defined. For shapes X and Y this is
where d(x,y) is the distance between points x and y.
2. Dual Hausdorff distance. This is whichever is larger of the Hausdorff distance between the two regions and the Hausdorff distance between their complements (i.e., the spaces outside the regions).
3. Symmetric difference distance. This is computed by dividing the area of the intersection of the two regions by the area of their union and subtracting the result from 1:
This takes the value 0 when the shapes are identical, and 1 when they do not overlap at all. (The quantity is called the Jaccard index and serves as a measure of similarity rather than distance.)
Distance measures are discussed in detail in Davis (2001).
Some shape measures can be expressed in terms of the similarity of the shape to some derived surrogate shape. For example, another measure of compactness (ranked fairly highly in MacEachren's study cited above) is the symmetric difference distance between the shape and a circle of the same area.
References:
Bunge, W. (1966). Theoretical Geography. Lund, Sweden: Lund University, C. W. K. Gleerup.
Davis, E. (2001). Continuous shape transformations and metrics of regions. Fundamenta Informaticae, 46, 31-54.
Duckham, M., Kulik, L., Worboys M., and Galton, A. (2008). Efficient generation of simple polygons for characterizing the shape of a set of points in the plane. Pattern Recognition, 41, 3224-3236. DOI: 10.1016/j.patcog.2008.03.023
Edelsbrunner, H., Kirkpatrick, D.G., and Seidel, R. (1983). On the shape of a set of points in the plane. IEEE Transactions on Information Theory, IT-29(4), 551-559.
Frolov, Yu. S. (1974). Measuring the shape of geographical phenomena: A history of the issue. In Soviet Geography: Review and Translation (676-687). Originally published in Izvestiya Vsesoyuznogo Geogracheskogo Obshchestva, 1974.
Galton, A. (2013). Prolegomena to an ontology of shape. In O. Kutz, M. Bhatt, S. Borgo, & P. Santos (Eds.), Proceedings of the Second Interdisciplinary Workshop "The Shape of Things," Rio de Janeiro, Brazil, April 3-4, 2013. http://ceur-ws.org/Vol-1007/invited4.pdf.
Hu, M. K. (1962). Pattern recognition by moment invariants. IRE Transactions on Information Theory, IT-8, 179-187.
Li, W., Goodchild, M. F., & Church, R. (2013). An efficient measure of compactness for two-dimensional shapes and its application in regionalization problems. International Journal of Geographical Information Science, 27(6), 1227-1250. DOI: 10.1080/13658816.2012.752093
MacEachren, A. M. (1985). Compactness of geographic shape: Comparison and evaluation of measures. Geografiska Annaler: Series B, Human Geography, 67(1), 53-67.
Prokop, R. J. & Reeves, A. P. (1992). A survey of moment-based techniques for unoccluded object representation and recognition. CVGIP: Graphical Models and Image Processing, 54(5), 438-460.
Sonka, M., Havac, V., & Boyle R. (1999). Image Processing, Analysis, and Machine Vision. Brooks/Cole, 2nd edition.
Teague, M. R. (1980). Image analysis via the general theory of moments. Journal of the Optical Society of America, 70(8), 920-930.
Zhang, C. & Atkinson, P. M. (2016). Novel shape indices for vector landscape pattern analysis. International Journal of Geographical Information Science, 30(12), 2442-2461. DOI: 10.1080/13658816.2016.1179313
Learning Objectives:
Describe ways in which the shape of a geographical entity can affect other characteristics of that entity.
Be familiar with a number of numerical shape descriptors, and appreciate that no one such descriptor can provide complete information about a shape.
Demonstrate understanding of moment-based approaches to shape by computing low-order moments for some simple examples.
Demonstrate understanding of a number of different types of shape surrogate by computing them for some simple examples and interpreting the results.
Determine the degree of similarity between shapes using a number of standard measures.
Instructional Assessment Questions:
Investigate examples of how the shape of a region affects its geographical characteristics; consider e.g., the structure of communication links and settlement patterns in a long thin country vs a roughly circular one.
Compute values of the various numerical shape descriptors listed in this article for a number of example shapes, including both simple geometrical shapes (e.g., triangles, rectangles, circles, ellipses) and actual geographical regions (e.g., different countries). Investigate to what extent similar-looking shapes tend to have similar values for the various different descriptors.
Computing moments. Consider the shape in discrete space comprising the points with coordinates (2,4), (3,2), (3,3), (3,4), (3,5), (3,6), (4,3), (4,4), (4,5), (4,6), (4,7), (5,5), (5,6), (5,7), (6,6), and (6,7). Compute the zeroth- and first-order moments. The first-order moments give you the coordinates of the shape's centroid; subtract these from each point to give the shape shifted so that its centroid is at the origin. With the shifted shape, compute the second-order moments, and use these to determine the principal axes of the shape, and the image ellipse. [You will need to consult a source such as Prokop and Reeves (1992) for details of how to find the principal axes and image ellipse.]
Two well-known algorithms for computing the convex hull of a shape are the Jarvis March (also known as the Gift-wrap Algorithm) and Graham's Scan. Find descriptions of these algorithms and implement them either in the form of computer programs or by working through them by hand. Investigate other algorithms for computing convex hulls. Extend your investigation to include non-convex hulls [the reference Duckham et al. (2008) provides a useful starting point].
Suppose we want to use one of the similarity measures dened in the article to compare the shapes of, say, different countries. Discuss what you would need to do in order to accomplish this. Try it!
Additional Resources:
Boyce, R. R. & Clarke, W. A. V. (1964). The concept of shape in geography. Geographical Review, 54(4), 561-572.
Clarke, W. A., V. & Gaile, G. L. (1973). The analysis and recognition of shapes. Geografiska Annaler. Series B. Human Geography, 55(2), 153-163.
Clementini, E. & Di Felice, P. (1997). A global framework for qualitative shape description. GeoInformatica,1, 11-27.
Lee, D. R. & Sallee, G. T. (1970). A method of measuring shape. Geographical Review, 60(4), 555-563.
Wentz, E. A. (1997). Shape analysis in GIS. Auto-Carto, 13, 204-213.
You are currently viewing an archived version of Topic Shape. If updates or revisions have been published you can find them at Shape.
Shape is important in GI Science because the shape of a geographical entity can have far-reaching effects on significant characteristics of that entity. In geography we are mainly concerned with two-dimensional shapes such as the outlines of islands, lakes, and administrative areas, but three-dimensional shapes may become important, for example in the treatment of landforms. Since the attribute of shape has infinitely many degrees of freedom, there can be no single numerical measure such that closely similar shapes are assigned close numerical values. Therefore different shape descriptors have been proposed for different purposes. Although it is generally desirable for a shape descriptor to be scale invariant and rotation invariant, not all proposed descriptors satisfy both these requirements. Some methods by which a shape is described using a single number are described, followed by a discussion of moment-based approaches. It is often useful to represent a complex shape by means of a surrogate shape of simpler form which facilitates storage, manipulation, and comparison between shapes; some examples of commonly used shape surrogates are presented. Another important task is to compare different shapes to determine how similar they are. The article concludes with a discussion of a number of such measures of similarity.
Galton, A. (2017). Shape. The Geographic Information Science & Technology Body of Knowledge (4th Quarter 2017 Edition), John P. Wilson (ed.). DOI: 10.22224/gistbok/2017.4.8.
This version was published on November 16, 2017.
This Topic is also available in the following editions: DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Shape. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital)
1. What is Shape?
Shape is important in GI Science because the shape of a geographical entity can have far-reaching effects on significant characteristics of that entity. Compare, for example, a long thin island with a roughly circular one. In the former a much greater proportion of the land area will be close to the coast, and the major communication links will tend to be parallel to the long axis. These factors may have an impact on vegetation, settlement patterns, trading relations, and much else. In general the shapes of geographical regions are relevant when we consider such things as urban form, trade areas, political units, drainage basins, and habitats. The problem for GI Science is how to characterize the shapes of geographical entities in ways that usefully capture such implications and are amenable to digital manipulation.
In the first instance we should distinguish between physical and mathematical shape. In fact, as discussed in Galton (2013), physical shape is not well defined because "same measurable shape as" is not an equivalence relation on physical entities, in contrast to "same mathematical shape as," which is an equivalence relation on mathematically defined entities. Here we take shape in GI Science to refer to the well-defined mathematical shapes of digital representations of real physical entities, e.g., of the polygons used to represent areal objects in GIS. The use of polygons is justified by the fact that one can approximate any shape arbitrarily closely by using a polygon with sufficiently many vertices (see, e.g., Bunge 1966, who shows further that a shape can be approximated arbitrarily closely by means of equilateral polygons).
In the geographical world we are mainly concerned with two-dimensional shapes such as the outlines of islands, lakes, and administrative areas. But three-dimensional shapes may become important in a discussion of landforms, or when working at a large scale where the vertical dimension of buildings may become important. In this article we shall confine ourselves to a discussion of shape in two dimensions, although many of the ideas we discuss will readily generalize from the two-dimensional case to the three-dimensional (e.g., replacing polygons by polyhedra).
2. Shape Descriptors
A key feature of shape as an attribute is that it has infinitely many degrees of freedom. This implies that there can be no single numerical measure such that closely similar shapes are assigned close numerical values. As stated by Frolov (1974), "[i]t is obviously fruitless to search for a single universal shape index." One way round this is to use a vector of distinct shape indices, analogous to the use of (red,green,blue) or (hue,saturation,lightness) for representing colour-spaces, which are also intrinsically multi-dimensional. Frolov specifically proposed compactness, dissection, and indentation for this, claiming them to be independent (hence orthogonal) measures.
It is generally - but not always - regarded as desirable for a shape descriptor to be scale invariant and rotation invariant. However, some proposed descriptors fail one or both of these tests. If A is the area of a shape and P its perimeter, then a measure of the form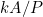 is not scale-invariant, whereas measures such as
is not scale-invariant, whereas measures such as 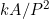 or
or 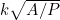 are. In the following, we use
are. In the following, we use 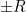 and
and 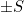 to indicate whether a measure is rotation invariant or scale invariant respectively.
to indicate whether a measure is rotation invariant or scale invariant respectively.
Although rotation invariance is generally a desirable characteristic for a shape descriptor, it is worth noting that this is not always considered to be the case. Identically shaped islands, for example, may present different characteristics depending on the orientations of their long axes relative to the prevailing winds or local current flows (and indeed these flows will themselves be differently affected by the differently oriented islands). Arguably, though, the difference in this case has only to do with orientation, and therefore should not be considered an effect of shape as such.
Table 1. The values of some numerical shape descriptors for a selection of simple shapes, illustrating presence or absence of scale and rotation invariance.
2.1 Numerical shape descriptors
Here we cover methods by which a shape is described using a single number; as noted above, combinations of such measures can be used to provide more discriminating vectorial descriptors. Many such methods have been proposed. For some of these, e.g., elongation, rectangularity, and compactness, a number of alternative definitions have been proposed, often involving a higher degree of mathematical sophistication in order to overcome the shortcomings of the naïve definitions. The values of the first six measures listed here are tabulated for some simple figures in Table 1, illustrating in particular how scale- and rotation-invariance apply to some measures but not to others.
1. Area:
2. Perimeter:
3. Area / Perimeter:
4. Area / Perimeter2: . This has range
. This has range ![(0,\frac{1}{4\pi }]](https://latex.codecogs.com/gif.latex?%5Cinline%20%5Cdpi%7B100%7D%20%280%2C%5Cfrac%7B1%7D%7B4%5Cpi%20%7D%5D) , taking the value
, taking the value 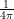 only for a circle. It is customary to scale up to (0, 1], using the measure
only for a circle. It is customary to scale up to (0, 1], using the measure 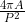 .
.
5. Aspect ratio. There are two possibilities here:
(a)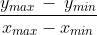 , i.e., the height/width ratio for the minimum axis-aligned bounding rectangle (-R, +S). This ranges over
, i.e., the height/width ratio for the minimum axis-aligned bounding rectangle (-R, +S). This ranges over 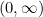 .
.
(b)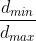 , where dmin and dmax are respectively the shorter and longer dimensions of the absolute (i.e., ot necessarily axis-aligned) minimum bounding rectangle (MBR), which is defined as the least-area rectangle, of any orientation, wholly covering the shape. This measure ranges over (0,1] , with 1 for shapes whose absolute MBR is a square. This measure is called elongatedness by Sonka et al. (1999).
, where dmin and dmax are respectively the shorter and longer dimensions of the absolute (i.e., ot necessarily axis-aligned) minimum bounding rectangle (MBR), which is defined as the least-area rectangle, of any orientation, wholly covering the shape. This measure ranges over (0,1] , with 1 for shapes whose absolute MBR is a square. This measure is called elongatedness by Sonka et al. (1999).
6. Elongation: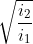 , where i1 and i2 are the second moments of the shape about its principle axes. (For the meaning of "moments" see section 2.2.)
, where i1 and i2 are the second moments of the shape about its principle axes. (For the meaning of "moments" see section 2.2.)
7. Compactness: This term has been used to describe many different measures. MacEachren (1985) systematically compares 11 proposed measures for compactness and evaluates them with respect to how well they correlate with homogeneity of superposed distributions. The "winning" measure is , where
, where 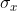 and
and 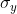 are the variances of the x and y coordinates of the points within the shape (+R, +S). Further measures of compactness are discussed by Li et al. (2013), who also introduce their own moment-based approach.
are the variances of the x and y coordinates of the points within the shape (+R, +S). Further measures of compactness are discussed by Li et al. (2013), who also introduce their own moment-based approach.
8. Eccentricity (Sonka et al. 1999) is the ratio of the maximum chord A to the longest chord B that is perpendicular to A (+R, +S). These do not necessarily agree with the sides of the absolute MBR, so although it is closely related to it, eccentricity is not the same as aspect ratio.
9. Rectangularity (Sonka et al. 1999) is the ratio of the shape's area to that of its absolute MBR. This has values in the range (0,1], with 1 attained when the shape is a rectangle (+R, +S).
2.2 Moment-based approaches
In a binary image, for a shape S whose centroid is located at the origin, the (p,q)th moment (where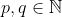 ) is the integral:
) is the integral:
Here S(x, y) is understood to be a function which takes the value 1 for points belonging to the shape, and 0 otherwise; this can be generalised to shapes with "fuzzy" membership, using 0 < S (x, y) < 1.
For digital images, which are discrete and finite, the integral can be replaced for computational purposes by the sum:
The nth-order moments are those in the set { }.
}.
A complete set of moments of all orders characterizes the shape uniquely; this is an infinite set, reflecting the infinitely many degrees of freedom mentioned above. The low-order moments provide important global information about the shape, whereas the higher-order moments increasingly reflect fine details. For the purpose of quantifying the most salient features for applications such as shape recognition or approximation, just the lower order moments suffice:
1. The zeroth order moment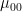 of a binary shape is just its area.
of a binary shape is just its area.
2. The first-order moments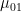 and
and 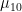 are zero for a shape centered at the origin, but for other shapes they indicate the position of the centroid.
are zero for a shape centered at the origin, but for other shapes they indicate the position of the centroid.
3. The second-order moments can be used to compute the "image ellipse," that is an "inertially equivalent" elliptical approximation to the shape, and also the principal axes of the shape and its radii of gyration.
4. The third-order moments allow computation of the skewness of the shape, that is, its degree of deviation from symmetry about the centroid (for its projections on the coordinate axes).
5. The fourth-order moments give the kurtosis of the image projections, that is the "peakedness" of the projection.
For further details, see Hu (1962), Teague (1980), and Prokop & Reeves (1992).
3. Shape Surrogates
For many purposes it is convenient to represent a complex shape by means of a "surrogate" shape of simpler form which facilitates storage, manipulation, and comparison between shapes. A generally desirable property of such surrogates is ease of computation. The properties of rotation invariance and scale invariance must be interpreted somewhat differently here: rotation invariance now means that as a shape is rotated, its surrogate rotates with it, by the same amount, while remaining congruent; and scale invariance means that as a shape is enlarged, its surrogate is also enlarged, by the same amount. Examples of commonly used shape surrogates are:
1. Minimum bounding rectangle. As noted above, this comes in two forms, axis-aligned (-R, +S) and absolute (+R,+S).
2. Convex Hull (+R, +S). This is the smallest convex shape containing the given shape. It has well-researched mathematical and computational properties.
3. Various "non-convex" hulls (usually +R, +S). These are designed to capture details that may be missed by the convex hull, such as the presence of large "bays" in the outline of a region, while still preserving tractable computational characteristics. Examples include the alpha-hull (Edelsbrunner 1983) and chi-hull (Duckham et al., 2008).
4. Quadtrees (-R, +S). The shape is inscribed in a square, which is divided into four quadrants. Each quadrant which includes part of the shape is marked "1," the remainder "0." The same procedure is recursively applied to each square marked with a "1" as many times as desired. This results in a compact tree structure, or "quadtree," from which the shape can be recovered at a level of detail corresponding to the depth of the recursion. The analogous construction in three dimensions is called an "octree."
5. Skeletons (+R,+S). A skeleton is a representation of a two-dimensional shape as a network of interior lines. A typical example, the topological skeleton, or medial axis, is the locus of centers of circles inscribed within the shape and tangent to it in two or more places. Figure 1 shows a shape and its medial axis together with a selection of the circles whose centers define it.
6. Image ellipse (+R,+S), as described above in the section on moment-based approaches.
This list is far from exhaustive, and researchers regularly come up with novel shape surrogates for different purposes - see for example Zhang & Atkinson (2016).
Figure 1. A shape with its medial axis and some of the circles whose centers define it.
Some of these shape surrogates can be applied not only to connected regions but also to the "virtual shapes" formed by patterns of disconnected point-like entities. Indeed, in the case of non-convex hulls, this is the primary application. Roughly speaking, this can be described as assigning a shape to the wood, given the positions of the trees.
4. Measures of Similarity Between Shapes
It is often required to compare different shapes to determine how similar they are. This can be used in image retrieval, where, for example, one might search for images of boats from an image collection by looking for shapes that are sufficiently similar to one of a set of "standard" boat images in a reference collection. In geography one can investigate how far similarly-shaped regions are similar in other respects as well, thereby determining which characteristics of regions are influenced by their shapes.
One way of measuring similarity is simply to take any of the numerical shape descriptors described above and compare its values for the shapes being compared. Another method is to take some measure of distance between regions and superpose the two shapes so that this distance is minimized. This gives a measure of difference rather than similarity. Examples of such distance measures are:
1. Hausdorff distance between two regions is the largest distance between any point in either one of the regions and the nearest point in the other; here the shapes are assumed to include their own boundary points, so that "largest" and "nearest" are well-defined. For shapes X and Y this is
where d(x,y) is the distance between points x and y.
2. Dual Hausdorff distance. This is whichever is larger of the Hausdorff distance between the two regions and the Hausdorff distance between their complements (i.e., the spaces outside the regions).
3. Symmetric difference distance. This is computed by dividing the area of the intersection of the two regions by the area of their union and subtracting the result from 1:
This takes the value 0 when the shapes are identical, and 1 when they do not overlap at all. (The quantity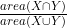 is called the Jaccard index and serves as a measure of similarity rather than distance.)
is called the Jaccard index and serves as a measure of similarity rather than distance.)
Distance measures are discussed in detail in Davis (2001).
Some shape measures can be expressed in terms of the similarity of the shape to some derived surrogate shape. For example, another measure of compactness (ranked fairly highly in MacEachren's study cited above) is the symmetric difference distance between the shape and a circle of the same area.
Bunge, W. (1966). Theoretical Geography. Lund, Sweden: Lund University, C. W. K. Gleerup.
Davis, E. (2001). Continuous shape transformations and metrics of regions. Fundamenta Informaticae, 46, 31-54.
Duckham, M., Kulik, L., Worboys M., and Galton, A. (2008). Efficient generation of simple polygons for characterizing the shape of a set of points in the plane. Pattern Recognition, 41, 3224-3236. DOI: 10.1016/j.patcog.2008.03.023
Edelsbrunner, H., Kirkpatrick, D.G., and Seidel, R. (1983). On the shape of a set of points in the plane. IEEE Transactions on Information Theory, IT-29(4), 551-559.
Frolov, Yu. S. (1974). Measuring the shape of geographical phenomena: A history of the issue. In Soviet Geography: Review and Translation (676-687). Originally published in Izvestiya Vsesoyuznogo Geogracheskogo Obshchestva, 1974.
Galton, A. (2013). Prolegomena to an ontology of shape. In O. Kutz, M. Bhatt, S. Borgo, & P. Santos (Eds.), Proceedings of the Second Interdisciplinary Workshop "The Shape of Things," Rio de Janeiro, Brazil, April 3-4, 2013. http://ceur-ws.org/Vol-1007/invited4.pdf.
Hu, M. K. (1962). Pattern recognition by moment invariants. IRE Transactions on Information Theory, IT-8, 179-187.
Li, W., Goodchild, M. F., & Church, R. (2013). An efficient measure of compactness for two-dimensional shapes and its application in regionalization problems. International Journal of Geographical Information Science, 27(6), 1227-1250. DOI: 10.1080/13658816.2012.752093
MacEachren, A. M. (1985). Compactness of geographic shape: Comparison and evaluation of measures. Geografiska Annaler: Series B, Human Geography, 67(1), 53-67.
Prokop, R. J. & Reeves, A. P. (1992). A survey of moment-based techniques for unoccluded object representation and recognition. CVGIP: Graphical Models and Image Processing, 54(5), 438-460.
Sonka, M., Havac, V., & Boyle R. (1999). Image Processing, Analysis, and Machine Vision. Brooks/Cole, 2nd edition.
Teague, M. R. (1980). Image analysis via the general theory of moments. Journal of the Optical Society of America, 70(8), 920-930.
Zhang, C. & Atkinson, P. M. (2016). Novel shape indices for vector landscape pattern analysis. International Journal of Geographical Information Science, 30(12), 2442-2461. DOI: 10.1080/13658816.2016.1179313
Boyce, R. R. & Clarke, W. A. V. (1964). The concept of shape in geography. Geographical Review, 54(4), 561-572.
Clarke, W. A., V. & Gaile, G. L. (1973). The analysis and recognition of shapes. Geografiska Annaler. Series B. Human Geography, 55(2), 153-163.
Clementini, E. & Di Felice, P. (1997). A global framework for qualitative shape description. GeoInformatica,1, 11-27.
Lee, D. R. & Sallee, G. T. (1970). A method of measuring shape. Geographical Review, 60(4), 555-563.
Wentz, E. A. (1997). Shape analysis in GIS. Auto-Carto, 13, 204-213.
Keywords: