AM-16 - Interpolation methods

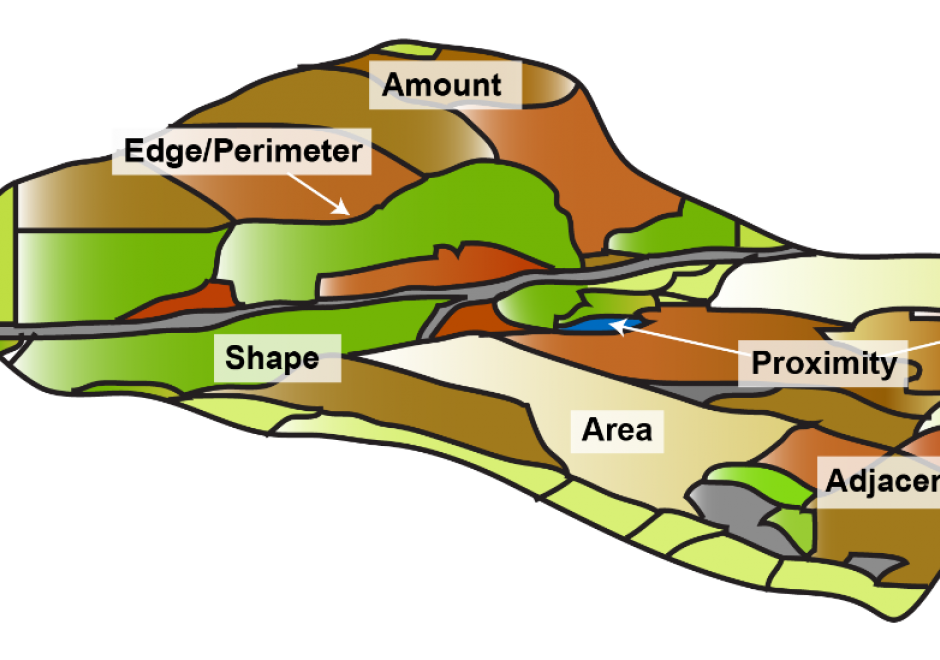
- Identify the spatial concepts that are assumed in different interpolation algorithms
- Compare and contrast interpolation by inverse distance weighting, bi-cubic spline fitting, and kriging
- Differentiate between trend surface analysis and deterministic spatial interpolation
- Explain why different interpolation algorithms produce different results and suggest ways by which these can be evaluated in the context of a specific problem
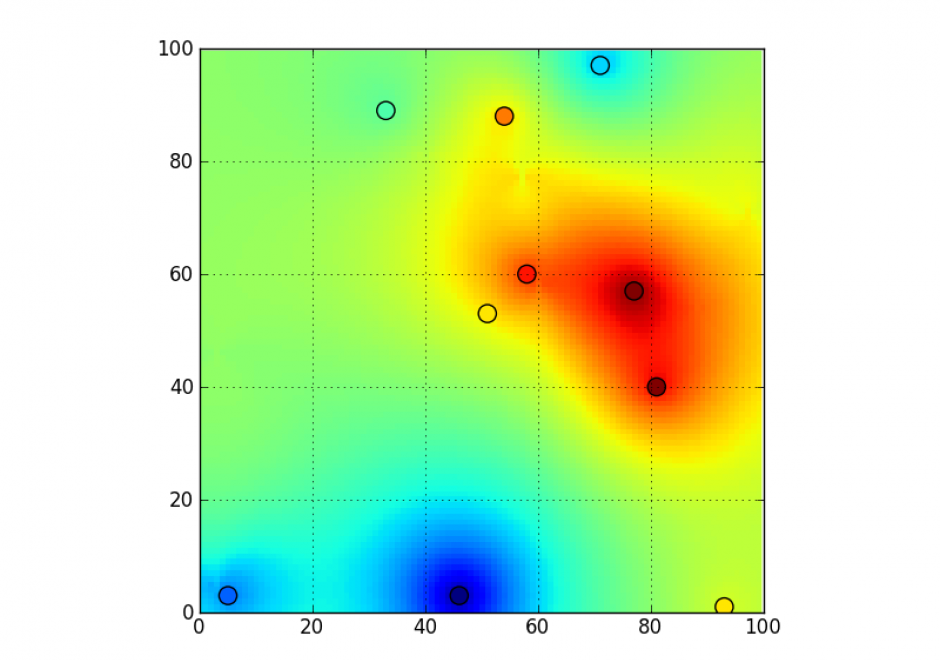
- Design an algorithm that interpolates irregular point elevation data onto a regular grid
- Outline algorithms to produce repeatable contour-type lines from point datasets using proximity polygons, spatial averages, or inverse distance weighting
- Implement a trend surface analysis using either the supplied function in a GIS or a regression function from any standard statistical package
- Describe how surfaces can be interpolated using splines
- Explain how the elevation values in a digital elevation model (DEM) are derived by interpolation from irregular arrays of spot elevations
- Discuss the pitfalls of using secondary data that has been generated using interpolations (e.g., Level 1 USGS DEMs)
- Estimate a value between two known values using linear interpolation (e.g., spot elevations, population between census years)

AM-16 - Interpolation methods