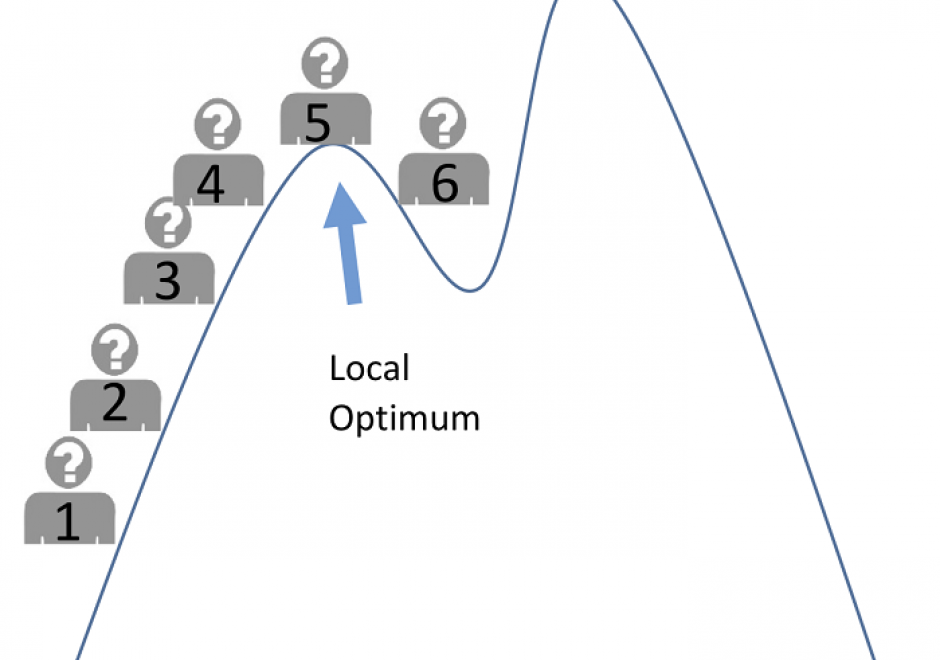
DM-27 - Genealogical relationships: lineage, inheritance

- Describe ways in which a geographic entity can be created from one or more others
- Discuss the effects of temporal scale on the modeling of genealogical structures
- Describe the genealogy (as identity-based change or temporal relationships) of particular geographic phenomena
- Determine whether it is important to represent the genealogy of entities for a particular application



PD-33 - GDAL/OGR and Geospatial Data IO Libraries
Manipulating (e.g., reading, writing, and processing) geospatial data, the first step in geospatial analysis tasks, is a complicated step, especially given the diverse types and formats of geospatial data combined with diverse spatial reference systems. Geospatial data Input/Output (IO) libraries help facilitate this step by handling some technical details of the IO process. GDAL/OGR is the most widely-used, broadly-supported, and constantly-updated free library among existing geospatial data IO libraries. GDAL/OGR provides a single raster abstract data model and a single vector abstract data model for processing and analyzing raster and vector geospatial data, respectively, and it supports most, if not all, commonly-used geospatial data formats. GDAL/OGR can also perform both cartographic projections on large scales and coordinate transformation for most of the spatial reference systems used in practice. This entry provides an overview of GDAL/OGR, including why we need such a geospatial data IO library and how it can be applied to various formats of geospatial data to support geospatial analysis tasks. Alternative geospatial data IO libraries are also introduced briefly. Future directions of development for GDAL/OGR and other geospatial data IO libraries in the age of big data and cloud computing are discussed as an epilogue to this entry.