Proper communication of spatial distributions, trends, and patterns in data is an important component of a cartographers work. Geospatial data is often large and complex, and due to inherent limitations of size, scalability, and sensitivity, cartographers are often required to work with data that is abstracted, aggregated, or simplified from its original form. Working with data in this manner serves to clarify cartographic messages, expedite design decisions, and assist in developing narratives, but it also introduces a degree of abstraction and subjectivity in the map that can make it easy to infer false messages from the data and ultimately can mislead map readers. This entry introduces the core topics of statistical mapping around cartography. First, we define enumeration and the aggregation of data to units of enumeration. Next, we introduce the importance of data normalization (or standardization) to more truthfully communicate cartographically and, lastly, discuss common methods of data classification and how cartographers bin data into groups that simplify communication.
Author and Citation Info:
Foster, M. (2019). Statistical Mapping (Enumeration, Normalization, Classification). The Geographic Information Science & Technology Body of Knowledge (2nd Quarter 2019 Edition), John P. Wilson (Ed.). DOI: 10.22224/gistbok/2019.2.2.
This entry was published on April 12, 2019.
This Topic is also available in the following editions: DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Data abstraction: classification, selection, and generalization. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers.(2nd Quarter 2016, first digital)
Enumeration: A complete, ordered quantitative listing of all spatial data items in a data collection. Enumerated data observations stand independent and can be quantified and collected into larger groups
Enumeration Unit: An areal unit by which enumerated data is aggregated and quantified.
Modifiable Areal Unit Problem: Differences between various types of enumeration units change how data is aggregated and can result in dramatic differences in display.
Ecological Fallacy: Arises when readers infer characteristics on individual data points based upon the aggregated category in which the data point, representing a logical fallacy where lower resolution data is used to infer properties of higher resolution data.
Normalization: The process of taking enumerated data and attempting to remove biases and misleading messages that are founded in differences between the enumeration units.
Classification: An intellectual process that groups similar phenomena to gain relative simplicity in communication and user interpretation. Also known as binning.
Classification Scheme: A systematic and scientific process used to split data into aggregated groups, or classes. The process can be algorithmic, arithmetic, geometric, or visual.
Communicating truthful and accurate messages distilled from large and complex geographic datasets is an important component of a cartographers work, and properly doing so involves a myriad of design decisions and display challenges. Geospatial data can be large and complex, and due to inherent limitations of size, scalability, and sensitivity, cartographers are often required to work with data that is modified, aggregated, simplified, or sampled from its original form. Working with data in this manner serves to clarify messages, expedite design decisions, and assist in developing narratives, but also introduces abstraction and subjectivity to the map that can make it easy to infer false messages from the data, and ultimately can mislead map readers.
Figure 1. Choropleth Map - 2016 U.S. Presidential Election. Source: New York Times, 2016.
The above figure, a well-known bivariate choropleth map featuring results of the 2016 United States Presidential Election, illustrates some of the pitfalls found in statistical mapping in cartography. At a glance, the overwhelming amount of dark red could indicate that the Republican party candidate (symbolized with red) received many more votes than the Democratic party candidate (symbolized with blue). However, based on population estimates from the U.S. Census the year of the election, the sum of the population in the counties colored blue is over 31,000,000 more than the sum of the counties colored red. While making the map, the cartographers chose to not normalize the map colors for population, meaning counties with 1,000,000 voters have the same color intensity as counties with 1,000 voters, potentially misleading readers. Cartographers and map makers must act sensibly in the cartographic message they are presenting to the reader, properly leveraging visual variables such as size, shape, hue, and saturation to best communicate the most truthful story around the data.
Many statistical display challenges are founded in data aggregation methods. Displaying too many individual points or including too many distinct features can overwhelm the display, confuse the message, and in some circumstances, even pose a threat to individual privacy. To properly view and communicate trends, single observations are regularly grouped with like or similar observations. These groupings can occur spatially, grouping nearby things with one another, and through data, grouping data values into categories of similar data relative to one another. The processes of grouping, also known as binning, is important in cartographic design and communication, and differences in methods can have a profound impact on the story and message of the map. Achieving the proper amount of aggregation and simplification is dependent on the message of the map. In the same way, showing too much can complicate the message, over-aggregation and oversimplification can serve the same detrimental effect and hide messages from the map reader.
This entry introduces the core topics of statistical mapping around cartography. In the following sections, we first define enumeration and the aggregation of data to units of enumeration. Next, we introduce the importance of data normalization (or standardization) to more honestly communicate and, lastly, introduce common methods of data classification and discuss how cartographers utilize these methods to simply display.
To be systematically analyzed and mapped in a consistent and standardized manner, geographic data must be enumerated. Geographic enumeration is a complete, ordered quantitative listing of all spatial data items in a data collection. Enumerated data are individually measured data observations that stand independent and can be quantified and collected into larger groups. Once a dataset is enumerated, it can be processed in a standardized manner for display. In Cartography, units by which enumerated data are aggregated are known as enumeration units. A common example of enumeration units is areal census units. Census data is aggregated into enumeration units that include blocks, block groups, census tracts, zip codes, and metropolitan areas, among many others. Individual enumerated data measurements are aggregated to these enumeration units to allow for privacy and to simplify the ability to distill patterns and trends based on counts and observations, many of which are not evident through the display of individual observations.
Figure 2. Counties as enumeration units for the 48 contiguous states of the U.S.Note the differences in size and shape across the extent. Source: U.S. Census Bureau TIGER data, 2017.
Enumerated and aggregated data can be communicated using many cartographic display representations, including choropleth, dot density, and graduated symbol. While important to consider when using any visualization method, enumeration units are particularly important in choropleth mapping, where the display of the data is intimately tied to the size and shape of the unit. Variations in the size and shape of an enumeration unit can drastically affect the message conveyed in the map. For example, San Bernardino County in southern California is larger by area than the four smallest U.S. states combined, and Los Angeles County alone has a higher population than 41 individual U.S. states.
To maintain a consistent cartographic message, displaying enumerated data works best when there is no significant variation in the size and shape of the enumerations units (Slocum, et al. 2009). Additionally, data that are unevenly distributed across an enumeration unit can be misleading and skew visual interpretations of distribution and pattern. Large areas can be perceived as ‘more important' and small areas as less, especially in choropleth mapping, and care should be taken in how the reader will interpret size in a cartographic composition.
Another important concept in data enumeration is known as the modifiable areal unit problem, often abbreviated as "MAUP." Differences between various types of enumeration units can change how data is aggregated, resulting in a dramatic difference in display and modifying the message of the map. For example, in the United States, ZIP codes and census tracts are common enumeration units for data aggregation; however, the geographies between the two units are often not consistent. Choose an enumeration unit that makes sense with the data being mapped is important to the cartographic process, and being consistent in the choice enumeration units is important when making comparisons over the extent of the map, both areal and temporal, and when creating series of maps.
Figure 3.The Modifiable Areal Unit Problem. Source: author.
Yet another pitfall related to enumeration units is that of ecological fallacy. In mapping, an ecological fallacy often arises when characteristics about individuals are inferred from aggregated data. In the MAUP example above, one can see that an individual data point can exist in varying categories depending on how the data is aggregated into enumeration units. The individual data point; however, does not change, therefore it is invalid to gather characteristics on data points from aggregated data. These aforementioned pitfalls all make a strong point for the need to account for differences in enumerated data to be partially accounted for through a process called normalization.
Data normalization (or standardization) is the process of taking enumerated data and attempting to remove biases and misleading messages that are founded in differences between the enumeration units. As discussed above, enumeration units will vary greatly in area, shape, quality, and quantity over space, making it a challenge to tell a consistent and robust story across the extent of the map. Differences between these units can mask messages in certain areas that might be quickly evident in others, and hinder the ability to compare units to one another. Normalization should be strongly considered in all types of aggregated mapping.
In cartography, there are two general types of normalization: statistical normalization and visual normalization. Statistical normalization seeks to account for differences through the data, and visual normalization seeks to account for limitations found in visual communication. In visual normalization, each of the visual variables can be explored to assist the reader in interpreting normalized data. Cartographers can normalize by adjusting saturation of color according to the data, known as a value-by-alpha map, or by modifying the size of an enumeration unit relative to the data, known as a value-by-area map, or cartogram (Roth, Woodruff, and Johnson, 2010). A value-by-alpha map might use higher saturation to represent enumeration units with a higher population, visually emphasizing areas with more intensity. A value-by-area map can effectively emphasize important individual enumeration units by exaggerating size, for example, showing areas with higher numbers as geometrically larger on the map, but risks losing geographic relation between features.
Statistical normalization is important when working with raw data containing total numbers of observations. Locations with high quantities of phenomena that can be mapped will naturally have a higher occurrence of individually measured phenomena. For example, a county with a higher total population is more likely to have a higher total number of persons experiencing a particular circumstance, because more people live in that county. The process of cartographic normalization is an effort to account for the aforementioned pitfalls by measuring densities and ratios rather than total numbers in an enumeration unit. This exposes areas where specific data observations might be higher or lower relative to the size or quantity of the enumeration unit. For illustration, normalization might expose that a unit with few people and therefore a low number of observed phenomena might actually be found to have a disproportionately high occurrence rate relative to the population of the county.
Normalization can be handled in the following five general ways: normalization by unit area, normalization by relevant population, normalization by summary value within a unit, normalization by summary value across units, and temporal normalization. These methods are illustrated in the following figures.
Figure 4. Normalization by Unit Area (Density). Source: author.
Figure 5. Normalization by Relevant Population (Rate). Source: author.
Figure 6.Normalization by Summary Value within the Unit (i.e. Mean, Median, Mode). Source: author.
Figure 7. Normalization by Summary Value across all Units (i.e. Above/Below Average, Standard Deviation). Source: author.
Figure 8. Normalization by a Prior Timestamp (i.e. Percent Change). Source: author.
In normalization, it is imperative that data are normalized against the same universe of values from which the enumerated phenomena was measured. For example, if the enumerated data being mapped is measured by household, normalization of a specific characteristic must be taken against the total number of households. This ensures that a proper density or ratio is displayed on the map that is not misleading or incorrect. Low-income households should be normalized against the total number of households, not against the total population number. A percentage of households calculated against the total number of persons is nonsensical, as they are entirely different units of measurement. Normalization, both statistical and visual, is important for truthful and effective cartographic communication of data.
Classification is an intellectual process that groups similar phenomena to gain relative simplicity in communication and user interpretation (Robinson et al., 1995; Longley et al., 2015). Classification, also referred to as binning, makes it easier to quickly extract values and view spatial trends and patterns in the data. There are a number of commonly used methods for data classification that place data observations into ‘bins' according to set algorithmic criteria, processing each enumerated data observation in the same manner to achieve the desired visual result. The bins are then used in the cartographic display of the map, simplifying complex data to better distill trends and patterns and make it easier for the map reader to interpret. Classification is perhaps most commonly thought of in creation of a choropleth map, but the technique is utilized in many types of maps, including dot density, pattern, graduated symbols, flow, and isoline. In each of these map types, visualizing data in an aggregated form allows the reader to more easily extract information and interpret a message from the map.
Figure 9. Data classification across different types of maps. Source: author.
Classification is an important and critical process in thematic storytelling and changing a classification scheme can modify the message of the map entirely. For example, using the same dataset and displaying it on two different maps using two different classification schemes can highlight and emphasize entirely different messages from the data. Certain methods might highlight outliers and hide nuances, where certain methods can display nuances but hide data outliers. The various methods produce different breaks between the classes. Dependent on the method used, sometimes these numbers can contain many decimal points. It is common practice to adjust class breaks to rounded numbers for easy interpretation and to improve legibility. The relationships of quantitative data within a should be considered when mapping. Qualitative data is often nominal, or categorical, and has no inherent ranking, but quantitative data will be fundamentally ordinal, interval, or ratio. Ordinal data can be grouped into generalized categories of low to high. Interval data has an arbitrary zero value, and this zero value is important to depict cartographically. A common example is temperature values. Ratio data has an absolute zero and data exist relative to the absolute zero. An example is data on the percentage of individuals unemployed (Kimerling, Muehrcke, Buckley, & Muehrcke, 2016).
Deciding on a classification scheme is an important component of map design and the chosen option depends on why the cartographer making the map (Krygier & Wood, 2016). There are many classification methodologies. Some of the most common ones include splitting data by equal intervals, quantiles, natural breaks, standard deviation, optimal breaks, maximum breaks, schemes that are unique to your purpose, or even just leaving the data unclassified.
The following examples utilize a single dataset to illustrate the impact that eight different classification methods have on the visual display of the map. The dataset enumerates the percent of residents over the age of 25 in Wisconsin that possess a Bachelor's degree or higher in Wisconsin in 2016 by County. In these maps, a county serves as the enumeration unit for aggregation and the educational data is normalized against the population over 25 years of age. There are 72 values in the dataset representing one for each county, and the range is from a minimum of 10% and a maximum of 50%. The data is based on the American Community Survey 5-year Estimates for educational achievement from 2012-2016 and is modified very slightly for simplicity of illustration (the highest value, Dane County, rounded up to 50% from 49%, and lowest value, Clark County, rounded down to 10% from 11%). The data is not heavily skewed, although there is a slight positive skew with some outliers.
Figure 10. Sample Dataset (Percentage of residents over the age of 25 in Wisconsin that possess a Bachelor's degree or higher in Wisconsin in 2016 by county, American Community Survey 5-year Estimates 2012-2016). Source: author.
Looking at this dataset mapped using eight different common classification methods with the ninth example unclassified, one can easily see the visual variations that the various classification methods have on the appearance of the map (Figure 11).
Figure 11. Common classification methods (Percentage of residents over the age of 25 in Wisconsin that possess a Bachelor's degree or higher in Wisconsin in 2016 by county). Data Source: United States Census Bureau / American FactFinder. “S1501 : Educational Attainment.” 2012-2016 American Community Survey. U.S. Census Bureau’s American Community Survey Office, 2018. Map Source: author.
Deciding which method is the right one to use is often a subjective task that should be made in relation to the dataset displayed and considering whether it is ordinal, interval, or ratio. Another important consideration is if there are any key breakpoints or numbers that should be included on the map. Let’s dig deeper into each of these types of classification mentioned above, describing each and identifying suggested use cases.
Class breaks at regular intervals along the number line at a set equivalent range. These breaks might be 20, 30, 40, etc, where each class is used to represent an equivalent range of measured data values. Classes are chosen regardless of the data. Equal interval is easy to read and understand; but it can be misleading in that no information is given on the distribution of the data within each distinct class.
Method is calculated by taking the highest data value minus the lowest data value, and dividing by the number of classes desired to get class breaks at equivalent intervals. In this case, subtract 10 from 50, then divide by 4 to get intervals of 10.
Uniformly distributed data with familiar data ranges.
Quantiles (Equal Count)
Equal numbers of data observations are placed into each category. Data is classified into groups like Top 20%, Upper-Middle 20%, Middle 20%, Lower-Middle 20%, and Bottom 20%. This method is easy for the map reader to understand. Because there are equal numbers of observations in each class, the map will always produce distinguishable patterns. It can be misleading in that equal numbers of data values are in each class, so outliers are lost.
Method is calculated by taking the total number of data values and dividing by the number of classes desired to get an equal number of data observations in each class. In this case, divide 72 by 4 to get 18 data observations in each class.
Evenly distributed data and ordinal data
Natural Breaks
Groups data according to natural groupings in the data values, minimizing differences between data values in the same class and maximizing differences between different classes (Slocum et al., 2009; Dent et al., 2008). It is a subjective method that works best with clustered datasets. This method allows the cartographer to group data and design the map classes, however due to its subjectivity the implementation can vary between cartographers.
Natural breaks classification is implemented through observing a histogram of data values then selecting class breaks according to peaks and valleys naturally fitting the curve of the dataset. In this theoretical example, the cartographer identifies natural valleys in the data and places three breaks to get four data classes.
Clustered data
Mean-Standard Deviation
Groups according to the distance to the mean standard deviation of the dataset. Using this method, the mean and standard deviation are taken from the dataset holistically, and the standard deviation from the mean is used to determine which class each data value falls in. This method is useful for normally distributed datasets in which classifying data as "above average" or "below average" makes a meaningful break in the data. This method does not work well with heavily skewed or non-normally distributed data.
Mean-Standard Deviation classification is implemented by calculating the mean value of the dataset and the standard deviation, placing class breaks at the mean value and each standard deviation value. In our example, calculate the mean and standard deviation of the 72 data values, place a break at the mean and place additional breaks at the standard deviations. The following class breaks were created using QGIS (2017).
Normally distributed data
Maximum Breaks
Breaks are placed at the largest intervals between adjacent data values.This is an easy to understand method that works best with piecewise datasets with gaps. This method does not work well with skewed data.
To implement, the data values are ordered from low to high and the difference between sequential data values are calculated. Breaks are placed where the differences are the largest, and the number of breaks is based on the number of classes desired. In our example, the largest breaks fall between 33 and 41 (8), 41 and 47, (6), and 47 and 50 (3), so we place our breaks at these points.
Piecewise and clustered data
Jenks-Caspall & Fisher-Jenks
Algorithmically optimal breaks are placed in data based on sums of deviations of means between individual classes. Initial breaks can be arbitrary and the algorithm is approached iteratively by moving values between classes until the smallest sum values are received (Slocum et al., 2005; Jenks, 1957). This minimizes variance within each class and maximizes variance between classes (Jiang, 2013).
With large datasets, the number of iterative steps needed to adjust classes can become prohibitive. The Fisher-Jenks Algorithm improves on the mathematical foundations by stating that an optimal partitioning of data can be identified by the sum of optimal partitions of subsets of data (Fisher, 1967). To implement on our dataset, arbitrarily select classes and calculate the deviations from means, adjusting values between classes until the smallses values are found. The Jenks Natural Breaks classification for this example was implemented using QGIS (2017).
Clustered and skewed data
Head/Tail Breaks
Algorithmically optimal breaks and the number of classes are based on the dataset itself. Head/Tails breaks works best on heavily tailed datasets, iterating through the data to minimize around the mean. From Jiang (2013), the head/tail breaks method groups the data values into two parts around the arithmetic mean and iteratively partitions until there are fewer higher values. Along the number line, the head represents the values above the mean and the tail below.
For a simple implementation of the Head/Tail Breaks classification, take all of the values and calculate the mean. Removing the values below the calculated mean, repeat the process on the larger values, calculating a new mean. Repeat this process until there are fewer data values larger than the mean than smaller than the mean within that iteration.
Heavily skewed data
Unique
Breaks determined by external criteria. This method disregards data values in the dataset and focuses on key values as breakpoints between classes. Using this method, breaks are determined through the context surrounding the data, which can be provided through literature, policy reviews, or external assessment to determine key data values, then data is grouped according to its relationship to these key values.
In our example, literature might support that key values are 15, 20, and 25. For unique breaks, we can set the classification values to these to call out observations based on important values.
Data where key numbers are important
References:
Dent, B. D., Torguson, J. S., & Hodler, T. W. (2008). Cartography: Thematic Map Design, 6th Edition. McGraw-Hill.
Fisher W. D. (1958). On grouping for maximum homogeneity, Journal of the American Statistical Association, 53, 789–798.
Jenks G. F. (1967). The data model concept in statistical mapping. International Yearbook of Cartography, 7, 186–190.
Jiang, B. (2013). Head/tail Breaks: A New Classification Scheme for Data with a Heavy-tailed Distribution. The Professional Geographer, 65, 482-494.
Kimerling, A. J., Muehrcke, J. O., Buckley, A. R., & Muehrcke, P. C. (2016). Map Use: Reading and Analysis, 8th ed., Esri Press Academic, Redlands, CA.
Krygier, J., & Wood, D. (2016). Making Maps: A Visual Guide to Map Design for GIS, 3rd Edition. New York, NY: The Guilford Press.
Longley, P. A., Goodchild, M. F., Maguire, D. J., & Rhind D. W. (2015). Geographic Information Science and Systems, 4th Edition. England: John Wiley & Sons, Ltd.
Robinson, A. H., Morrison, J. L., Muehrcke, P. C., Kimerling, A. J., & Guptill, S. C. (1995). Elements of Cartography, 6th ed. New York: John Wiley and Sons.
QGIS Development Team (2017). QGIS Geographic Information System. Open Source Geospatial Foundation Project. http://qgis.osgeo.org
Roth, R., Woodruff, A., & Johnson, Z. (2010). Value-by-alpha Maps: An Alternative Technique to the Cartogram. Cartographic Journal, 47(2), 130-40.
Slocum, T. A., McMaster, R. B., Kessler, F. C., & Howard, H. H. (2009). Thematic Cartography and Geovisualization, 3rd ed. Upper Saddle River, NJ: Pearson Prentice Hall.
United States Census Bureau / American FactFinder. “S1501 : Educational Attainment.” 2012-2016 American Community Survey. U.S. Census Bureau’s American Community Survey Office, 2018. Web. Accessed on August 18, 2018 from http://factfinder2.census.gov
United States Census Bureau / American FactFinder. “Summary File 1.” 2010 Census. U.S. Census Bureau, 2010. Web. Accessed on August 18, 2018 from http://factfinder2.census.gov
Learning Objectives:
Discuss advantages and disadvantages of various data classification methods for choropleth mapping, including equal interval, quantiles, mean-standard deviation, natural breaks, and “optimal” methods
Apply various techniques for normalizing data
Demonstrate how different classification schemes produce very different maps from a single set of interval- or ratio-level data
Write algorithms to perform equal interval, quantiles, mean-standard deviation, natural breaks, and “optimal” classification for choropleth mapping
Instructional Assessment Questions:
Explain the Modifiable Areal Unit Problem and describe how it can influence and impact cartographic communication.
Describe visual normalization and two of the methods in which it can be implemented.
You are provided data containing the total number of multigenerational households at a county level. Why might it be important to important to normalize this dataset?
What is the difference between ordinal, interval, and ratio data? Describe how you might depict these different types of data cartographically.
In selecting a classification scheme, what considerations should be taken when assessing the data?
What is a good classification scheme for displaying uniform data? Heavily-skewed data? Ordinal data? Clustered data? Normally distributed data?
Additional Resources:
Bertin, J. (1967/2010). Semiology of Graphics: Diagrams, Networks, Maps. trans. W. Berg. Redlands, CA: Esri Press.
Kraak, M. J., & Ormeling, F. J. (2010). Cartography – visualization of spatial data, 3rd ed., Harlow, Pearson Education Ltd.
MacEachren, A. M. (1995). How Maps Work: Representation, Visualization, and Design. The Guilford Press.
Dorling, D., & Fairbairn, D. (1997) Mapping Ways of Representing the World, London: Longman.
McGrew Jr., J. C., Lembo Jr., A. J., Monroe, C. B., & Soderstrom, P. An Introduction to Statistical Problem Solving in Geography. Waveland Press, Inc., 3 edition.
Lloyd, C. D. (2010). Spatial Data Analysis: An Introduction for GIS Users. New York: Oxford University Press.
Harrower, M., & Brewer, C. A. (2003). ColorBrewer.org: an online tool for selecting colour schemes for maps. The Cartographic Journal, 40(1), 27-37.
You are currently viewing an archived version of Topic Statistical Mapping (Enumeration, Normalization, Classification). If updates or revisions have been published you can find them at Statistical Mapping (Enumeration, Normalization, Classification).
Proper communication of spatial distributions, trends, and patterns in data is an important component of a cartographers work. Geospatial data is often large and complex, and due to inherent limitations of size, scalability, and sensitivity, cartographers are often required to work with data that is abstracted, aggregated, or simplified from its original form. Working with data in this manner serves to clarify cartographic messages, expedite design decisions, and assist in developing narratives, but it also introduces a degree of abstraction and subjectivity in the map that can make it easy to infer false messages from the data and ultimately can mislead map readers. This entry introduces the core topics of statistical mapping around cartography. First, we define enumeration and the aggregation of data to units of enumeration. Next, we introduce the importance of data normalization (or standardization) to more truthfully communicate cartographically and, lastly, discuss common methods of data classification and how cartographers bin data into groups that simplify communication.
Foster, M. (2019). Statistical Mapping (Enumeration, Normalization, Classification). The Geographic Information Science & Technology Body of Knowledge (2nd Quarter 2019 Edition), John P. Wilson (Ed.). DOI: 10.22224/gistbok/2019.2.2.
This entry was published on April 12, 2019.
This Topic is also available in the following editions: DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Data abstraction: classification, selection, and generalization. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital)
1. Definitions
Enumeration: A complete, ordered quantitative listing of all spatial data items in a data collection. Enumerated data observations stand independent and can be quantified and collected into larger groups
Enumeration Unit: An areal unit by which enumerated data is aggregated and quantified.
Modifiable Areal Unit Problem: Differences between various types of enumeration units change how data is aggregated and can result in dramatic differences in display.
Ecological Fallacy: Arises when readers infer characteristics on individual data points based upon the aggregated category in which the data point, representing a logical fallacy where lower resolution data is used to infer properties of higher resolution data.
Normalization: The process of taking enumerated data and attempting to remove biases and misleading messages that are founded in differences between the enumeration units.
Classification: An intellectual process that groups similar phenomena to gain relative simplicity in communication and user interpretation. Also known as binning.
Classification Scheme: A systematic and scientific process used to split data into aggregated groups, or classes. The process can be algorithmic, arithmetic, geometric, or visual.
2. Introduction
Communicating truthful and accurate messages distilled from large and complex geographic datasets is an important component of a cartographers work, and properly doing so involves a myriad of design decisions and display challenges. Geospatial data can be large and complex, and due to inherent limitations of size, scalability, and sensitivity, cartographers are often required to work with data that is modified, aggregated, simplified, or sampled from its original form. Working with data in this manner serves to clarify messages, expedite design decisions, and assist in developing narratives, but also introduces abstraction and subjectivity to the map that can make it easy to infer false messages from the data, and ultimately can mislead map readers.
The above figure, a well-known bivariate choropleth map featuring results of the 2016 United States Presidential Election, illustrates some of the pitfalls found in statistical mapping in cartography. At a glance, the overwhelming amount of dark red could indicate that the Republican party candidate (symbolized with red) received many more votes than the Democratic party candidate (symbolized with blue). However, based on population estimates from the U.S. Census the year of the election, the sum of the population in the counties colored blue is over 31,000,000 more than the sum of the counties colored red. While making the map, the cartographers chose to not normalize the map colors for population, meaning counties with 1,000,000 voters have the same color intensity as counties with 1,000 voters, potentially misleading readers. Cartographers and map makers must act sensibly in the cartographic message they are presenting to the reader, properly leveraging visual variables such as size, shape, hue, and saturation to best communicate the most truthful story around the data.
Many statistical display challenges are founded in data aggregation methods. Displaying too many individual points or including too many distinct features can overwhelm the display, confuse the message, and in some circumstances, even pose a threat to individual privacy. To properly view and communicate trends, single observations are regularly grouped with like or similar observations. These groupings can occur spatially, grouping nearby things with one another, and through data, grouping data values into categories of similar data relative to one another. The processes of grouping, also known as binning, is important in cartographic design and communication, and differences in methods can have a profound impact on the story and message of the map. Achieving the proper amount of aggregation and simplification is dependent on the message of the map. In the same way, showing too much can complicate the message, over-aggregation and oversimplification can serve the same detrimental effect and hide messages from the map reader.
This entry introduces the core topics of statistical mapping around cartography. In the following sections, we first define enumeration and the aggregation of data to units of enumeration. Next, we introduce the importance of data normalization (or standardization) to more honestly communicate and, lastly, introduce common methods of data classification and discuss how cartographers utilize these methods to simply display.
3. Enumeration
To be systematically analyzed and mapped in a consistent and standardized manner, geographic data must be enumerated. Geographic enumeration is a complete, ordered quantitative listing of all spatial data items in a data collection. Enumerated data are individually measured data observations that stand independent and can be quantified and collected into larger groups. Once a dataset is enumerated, it can be processed in a standardized manner for display. In Cartography, units by which enumerated data are aggregated are known as enumeration units. A common example of enumeration units is areal census units. Census data is aggregated into enumeration units that include blocks, block groups, census tracts, zip codes, and metropolitan areas, among many others. Individual enumerated data measurements are aggregated to these enumeration units to allow for privacy and to simplify the ability to distill patterns and trends based on counts and observations, many of which are not evident through the display of individual observations.
Enumerated and aggregated data can be communicated using many cartographic display representations, including choropleth, dot density, and graduated symbol. While important to consider when using any visualization method, enumeration units are particularly important in choropleth mapping, where the display of the data is intimately tied to the size and shape of the unit. Variations in the size and shape of an enumeration unit can drastically affect the message conveyed in the map. For example, San Bernardino County in southern California is larger by area than the four smallest U.S. states combined, and Los Angeles County alone has a higher population than 41 individual U.S. states.
To maintain a consistent cartographic message, displaying enumerated data works best when there is no significant variation in the size and shape of the enumerations units (Slocum, et al. 2009). Additionally, data that are unevenly distributed across an enumeration unit can be misleading and skew visual interpretations of distribution and pattern. Large areas can be perceived as ‘more important' and small areas as less, especially in choropleth mapping, and care should be taken in how the reader will interpret size in a cartographic composition.
Another important concept in data enumeration is known as the modifiable areal unit problem, often abbreviated as "MAUP." Differences between various types of enumeration units can change how data is aggregated, resulting in a dramatic difference in display and modifying the message of the map. For example, in the United States, ZIP codes and census tracts are common enumeration units for data aggregation; however, the geographies between the two units are often not consistent. Choose an enumeration unit that makes sense with the data being mapped is important to the cartographic process, and being consistent in the choice enumeration units is important when making comparisons over the extent of the map, both areal and temporal, and when creating series of maps.
Figure 3. The Modifiable Areal Unit Problem. Source: author.
Yet another pitfall related to enumeration units is that of ecological fallacy. In mapping, an ecological fallacy often arises when characteristics about individuals are inferred from aggregated data. In the MAUP example above, one can see that an individual data point can exist in varying categories depending on how the data is aggregated into enumeration units. The individual data point; however, does not change, therefore it is invalid to gather characteristics on data points from aggregated data. These aforementioned pitfalls all make a strong point for the need to account for differences in enumerated data to be partially accounted for through a process called normalization.
4. Normalization
Data normalization (or standardization) is the process of taking enumerated data and attempting to remove biases and misleading messages that are founded in differences between the enumeration units. As discussed above, enumeration units will vary greatly in area, shape, quality, and quantity over space, making it a challenge to tell a consistent and robust story across the extent of the map. Differences between these units can mask messages in certain areas that might be quickly evident in others, and hinder the ability to compare units to one another. Normalization should be strongly considered in all types of aggregated mapping.
In cartography, there are two general types of normalization: statistical normalization and visual normalization. Statistical normalization seeks to account for differences through the data, and visual normalization seeks to account for limitations found in visual communication. In visual normalization, each of the visual variables can be explored to assist the reader in interpreting normalized data. Cartographers can normalize by adjusting saturation of color according to the data, known as a value-by-alpha map, or by modifying the size of an enumeration unit relative to the data, known as a value-by-area map, or cartogram (Roth, Woodruff, and Johnson, 2010). A value-by-alpha map might use higher saturation to represent enumeration units with a higher population, visually emphasizing areas with more intensity. A value-by-area map can effectively emphasize important individual enumeration units by exaggerating size, for example, showing areas with higher numbers as geometrically larger on the map, but risks losing geographic relation between features.
Statistical normalization is important when working with raw data containing total numbers of observations. Locations with high quantities of phenomena that can be mapped will naturally have a higher occurrence of individually measured phenomena. For example, a county with a higher total population is more likely to have a higher total number of persons experiencing a particular circumstance, because more people live in that county. The process of cartographic normalization is an effort to account for the aforementioned pitfalls by measuring densities and ratios rather than total numbers in an enumeration unit. This exposes areas where specific data observations might be higher or lower relative to the size or quantity of the enumeration unit. For illustration, normalization might expose that a unit with few people and therefore a low number of observed phenomena might actually be found to have a disproportionately high occurrence rate relative to the population of the county.
Normalization can be handled in the following five general ways: normalization by unit area, normalization by relevant population, normalization by summary value within a unit, normalization by summary value across units, and temporal normalization. These methods are illustrated in the following figures.
Figure 4. Normalization by Unit Area (Density). Source: author.
Figure 5. Normalization by Relevant Population (Rate). Source: author.
Figure 6. Normalization by Summary Value within the Unit (i.e. Mean, Median, Mode). Source: author.
Figure 7. Normalization by Summary Value across all Units (i.e. Above/Below Average, Standard Deviation). Source: author.
Figure 8. Normalization by a Prior Timestamp (i.e. Percent Change). Source: author.
In normalization, it is imperative that data are normalized against the same universe of values from which the enumerated phenomena was measured. For example, if the enumerated data being mapped is measured by household, normalization of a specific characteristic must be taken against the total number of households. This ensures that a proper density or ratio is displayed on the map that is not misleading or incorrect. Low-income households should be normalized against the total number of households, not against the total population number. A percentage of households calculated against the total number of persons is nonsensical, as they are entirely different units of measurement. Normalization, both statistical and visual, is important for truthful and effective cartographic communication of data.
5. Classification
Classification is an intellectual process that groups similar phenomena to gain relative simplicity in communication and user interpretation (Robinson et al., 1995; Longley et al., 2015). Classification, also referred to as binning, makes it easier to quickly extract values and view spatial trends and patterns in the data. There are a number of commonly used methods for data classification that place data observations into ‘bins' according to set algorithmic criteria, processing each enumerated data observation in the same manner to achieve the desired visual result. The bins are then used in the cartographic display of the map, simplifying complex data to better distill trends and patterns and make it easier for the map reader to interpret. Classification is perhaps most commonly thought of in creation of a choropleth map, but the technique is utilized in many types of maps, including dot density, pattern, graduated symbols, flow, and isoline. In each of these map types, visualizing data in an aggregated form allows the reader to more easily extract information and interpret a message from the map.
Figure 9. Data classification across different types of maps. Source: author.
Classification is an important and critical process in thematic storytelling and changing a classification scheme can modify the message of the map entirely. For example, using the same dataset and displaying it on two different maps using two different classification schemes can highlight and emphasize entirely different messages from the data. Certain methods might highlight outliers and hide nuances, where certain methods can display nuances but hide data outliers. The various methods produce different breaks between the classes. Dependent on the method used, sometimes these numbers can contain many decimal points. It is common practice to adjust class breaks to rounded numbers for easy interpretation and to improve legibility. The relationships of quantitative data within a should be considered when mapping. Qualitative data is often nominal, or categorical, and has no inherent ranking, but quantitative data will be fundamentally ordinal, interval, or ratio. Ordinal data can be grouped into generalized categories of low to high. Interval data has an arbitrary zero value, and this zero value is important to depict cartographically. A common example is temperature values. Ratio data has an absolute zero and data exist relative to the absolute zero. An example is data on the percentage of individuals unemployed (Kimerling, Muehrcke, Buckley, & Muehrcke, 2016).
Deciding on a classification scheme is an important component of map design and the chosen option depends on why the cartographer making the map (Krygier & Wood, 2016). There are many classification methodologies. Some of the most common ones include splitting data by equal intervals, quantiles, natural breaks, standard deviation, optimal breaks, maximum breaks, schemes that are unique to your purpose, or even just leaving the data unclassified.
The following examples utilize a single dataset to illustrate the impact that eight different classification methods have on the visual display of the map. The dataset enumerates the percent of residents over the age of 25 in Wisconsin that possess a Bachelor's degree or higher in Wisconsin in 2016 by County. In these maps, a county serves as the enumeration unit for aggregation and the educational data is normalized against the population over 25 years of age. There are 72 values in the dataset representing one for each county, and the range is from a minimum of 10% and a maximum of 50%. The data is based on the American Community Survey 5-year Estimates for educational achievement from 2012-2016 and is modified very slightly for simplicity of illustration (the highest value, Dane County, rounded up to 50% from 49%, and lowest value, Clark County, rounded down to 10% from 11%). The data is not heavily skewed, although there is a slight positive skew with some outliers.
Figure 10. Sample Dataset (Percentage of residents over the age of 25 in Wisconsin that possess a Bachelor's degree or higher in Wisconsin in 2016 by county, American Community Survey 5-year Estimates 2012-2016). Source: author.
Looking at this dataset mapped using eight different common classification methods with the ninth example unclassified, one can easily see the visual variations that the various classification methods have on the appearance of the map (Figure 11).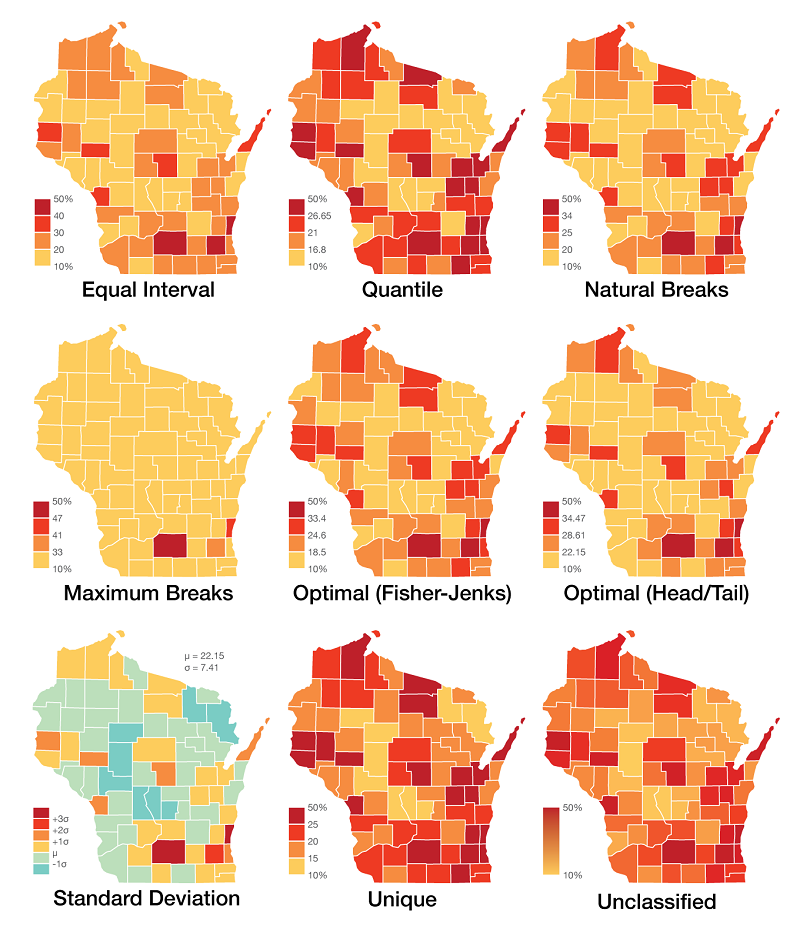
Figure 11. Common classification methods (Percentage of residents over the age of 25 in Wisconsin that possess a Bachelor's degree or higher in Wisconsin in 2016 by county). Data Source: United States Census Bureau / American FactFinder. “S1501 : Educational Attainment.” 2012-2016 American Community Survey. U.S. Census Bureau’s American Community Survey Office, 2018. Map Source: author.
Deciding which method is the right one to use is often a subjective task that should be made in relation to the dataset displayed and considering whether it is ordinal, interval, or ratio. Another important consideration is if there are any key breakpoints or numbers that should be included on the map. Let’s dig deeper into each of these types of classification mentioned above, describing each and identifying suggested use cases.
6. Classification Methods
Class breaks at regular intervals along the number line at a set equivalent range. These breaks might be 20, 30, 40, etc, where each class is used to represent an equivalent range of measured data values. Classes are chosen regardless of the data. Equal interval is easy to read and understand; but it can be misleading in that no information is given on the distribution of the data within each distinct class.
Method is calculated by taking the highest data value minus the lowest data value, and dividing by the number of classes desired to get class breaks at equivalent intervals. In this case, subtract 10 from 50, then divide by 4 to get intervals of 10.
Equal numbers of data observations are placed into each category. Data is classified into groups like Top 20%, Upper-Middle 20%, Middle 20%, Lower-Middle 20%, and Bottom 20%. This method is easy for the map reader to understand. Because there are equal numbers of observations in each class, the map will always produce distinguishable patterns. It can be misleading in that equal numbers of data values are in each class, so outliers are lost.
Method is calculated by taking the total number of data values and dividing by the number of classes desired to get an equal number of data observations in each class. In this case, divide 72 by 4 to get 18 data observations in each class.
Groups data according to natural groupings in the data values, minimizing differences between data values in the same class and maximizing differences between different classes (Slocum et al., 2009; Dent et al., 2008). It is a subjective method that works best with clustered datasets. This method allows the cartographer to group data and design the map classes, however due to its subjectivity the implementation can vary between cartographers.
Natural breaks classification is implemented through observing a histogram of data values then selecting class breaks according to peaks and valleys naturally fitting the curve of the dataset. In this theoretical example, the cartographer identifies natural valleys in the data and places three breaks to get four data classes.
Groups according to the distance to the mean standard deviation of the dataset. Using this method, the mean and standard deviation are taken from the dataset holistically, and the standard deviation from the mean is used to determine which class each data value falls in. This method is useful for normally distributed datasets in which classifying data as "above average" or "below average" makes a meaningful break in the data. This method does not work well with heavily skewed or non-normally distributed data.
Mean-Standard Deviation classification is implemented by calculating the mean value of the dataset and the standard deviation, placing class breaks at the mean value and each standard deviation value. In our example, calculate the mean and standard deviation of the 72 data values, place a break at the mean and place additional breaks at the standard deviations. The following class breaks were created using QGIS (2017).
Breaks are placed at the largest intervals between adjacent data values.This is an easy to understand method that works best with piecewise datasets with gaps. This method does not work well with skewed data.
To implement, the data values are ordered from low to high and the difference between sequential data values are calculated. Breaks are placed where the differences are the largest, and the number of breaks is based on the number of classes desired. In our example, the largest breaks fall between 33 and 41 (8), 41 and 47, (6), and 47 and 50 (3), so we place our breaks at these points.
Algorithmically optimal breaks are placed in data based on sums of deviations of means between individual classes. Initial breaks can be arbitrary and the algorithm is approached iteratively by moving values between classes until the smallest sum values are received (Slocum et al., 2005; Jenks, 1957). This minimizes variance within each class and maximizes variance between classes (Jiang, 2013).
With large datasets, the number of iterative steps needed to adjust classes can become prohibitive. The Fisher-Jenks Algorithm improves on the mathematical foundations by stating that an optimal partitioning of data can be identified by the sum of optimal partitions of subsets of data (Fisher, 1967). To implement on our dataset, arbitrarily select classes and calculate the deviations from means, adjusting values between classes until the smallses values are found. The Jenks Natural Breaks classification for this example was implemented using QGIS (2017).
Algorithmically optimal breaks and the number of classes are based on the dataset itself. Head/Tails breaks works best on heavily tailed datasets, iterating through the data to minimize around the mean. From Jiang (2013), the head/tail breaks method groups the data values into two parts around the arithmetic mean and iteratively partitions until there are fewer higher values. Along the number line, the head represents the values above the mean and the tail below.
For a simple implementation of the Head/Tail Breaks classification, take all of the values and calculate the mean. Removing the values below the calculated mean, repeat the process on the larger values, calculating a new mean. Repeat this process until there are fewer data values larger than the mean than smaller than the mean within that iteration.
Breaks determined by external criteria. This method disregards data values in the dataset and focuses on key values as breakpoints between classes. Using this method, breaks are determined through the context surrounding the data, which can be provided through literature, policy reviews, or external assessment to determine key data values, then data is grouped according to its relationship to these key values.
In our example, literature might support that key values are 15, 20, and 25. For unique breaks, we can set the classification values to these to call out observations based on important values.
Dent, B. D., Torguson, J. S., & Hodler, T. W. (2008). Cartography: Thematic Map Design, 6th Edition. McGraw-Hill.
Fisher W. D. (1958). On grouping for maximum homogeneity, Journal of the American Statistical Association, 53, 789–798.
Jenks G. F. (1967). The data model concept in statistical mapping. International Yearbook of Cartography, 7, 186–190.
Jiang, B. (2013). Head/tail Breaks: A New Classification Scheme for Data with a Heavy-tailed Distribution. The Professional Geographer, 65, 482-494.
Kimerling, A. J., Muehrcke, J. O., Buckley, A. R., & Muehrcke, P. C. (2016). Map Use: Reading and Analysis, 8th ed., Esri Press Academic, Redlands, CA.
Krygier, J., & Wood, D. (2016). Making Maps: A Visual Guide to Map Design for GIS, 3rd Edition. New York, NY: The Guilford Press.
Longley, P. A., Goodchild, M. F., Maguire, D. J., & Rhind D. W. (2015). Geographic Information Science and Systems, 4th Edition. England: John Wiley & Sons, Ltd.
Robinson, A. H., Morrison, J. L., Muehrcke, P. C., Kimerling, A. J., & Guptill, S. C. (1995). Elements of Cartography, 6th ed. New York: John Wiley and Sons.
QGIS Development Team (2017). QGIS Geographic Information System. Open Source Geospatial Foundation Project. http://qgis.osgeo.org
Roth, R., Woodruff, A., & Johnson, Z. (2010). Value-by-alpha Maps: An Alternative Technique to the Cartogram. Cartographic Journal, 47(2), 130-40.
Slocum, T. A., McMaster, R. B., Kessler, F. C., & Howard, H. H. (2009). Thematic Cartography and Geovisualization, 3rd ed. Upper Saddle River, NJ: Pearson Prentice Hall.
United States Census Bureau / American FactFinder. “S1501 : Educational Attainment.” 2012-2016 American Community Survey. U.S. Census Bureau’s American Community Survey Office, 2018. Web. Accessed on August 18, 2018 from http://factfinder2.census.gov
United States Census Bureau / American FactFinder. “Summary File 1.” 2010 Census. U.S. Census Bureau, 2010. Web. Accessed on August 18, 2018 from http://factfinder2.census.gov
Bertin, J. (1967/2010). Semiology of Graphics: Diagrams, Networks, Maps. trans. W. Berg. Redlands, CA: Esri Press.
Kraak, M. J., & Ormeling, F. J. (2010). Cartography – visualization of spatial data, 3rd ed., Harlow, Pearson Education Ltd.
MacEachren, A. M. (1995). How Maps Work: Representation, Visualization, and Design. The Guilford Press.
Dorling, D., & Fairbairn, D. (1997) Mapping Ways of Representing the World, London: Longman.
McGrew Jr., J. C., Lembo Jr., A. J., Monroe, C. B., & Soderstrom, P. An Introduction to Statistical Problem Solving in Geography. Waveland Press, Inc., 3 edition.
Lloyd, C. D. (2010). Spatial Data Analysis: An Introduction for GIS Users. New York: Oxford University Press.
Harrower, M., & Brewer, C. A. (2003). ColorBrewer.org: an online tool for selecting colour schemes for maps. The Cartographic Journal, 40(1), 27-37.
Keywords: