You are currently viewing an archived version of Topic Thematic Accuracy Assessment.
If updates or revisions have been published you can find them at Thematic Accuracy Assessment.
Geographic Information System (GIS) applications often involve various analytical techniques and geographic data to produce thematic maps for gaining a better understanding of geospatial situations to support spatial decisions. Accuracy assessment of a thematic map is necessary for evaluating the quality of the research results and ensuring appropriate use of the geographic data. Thematic accuracy deals with evaluating the accuracy of the attributes or labels of mapped features by comparing them to a reference that is assumed to be true. The fundamental practice presents the remote sensing approach to thematic accuracy assessment as a good guidance. For instance, the accuracy of a remote sensing image can be represented as an error matrix when the map and reference classification are conducted based on categories. This entry introduces basic concepts and techniques used in conducting thematic accuracy with an emphasis on land cover classification based on remote sensing images. The entry first introduces concepts of spatial uncertainty and spatial data quality standards and further gives an example of how spatial data quality affects thematic accuracy. Additionally, the entry illustrates the techniques that can be used to access thematic accuracy as well as using spatial autocorrelation in thematic accuracy sampling design.
Author and Citation Info:
Zhang, Z. (2020). Thematic Accuracy Assessment. The Geographic Information Science & Technology Body of Knowledge (2nd Quarter 2020 Edition), John P. Wilson (ed.). DOI: 10.22224/gistbok/2020.2.3.
This entry was published on June 12, 2020.
An earlier version can be found at:
DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Thematic accuracy. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital).
Uncertainty is an inherent attribute of geographic information and knowledge representation because perfect knowledge is hard to obtain (Goodchild 1992; Longley 2005). Any collection of observational geographical information is prone to uncertainty in several forms. Generally, there are two types of map accuracy assessments: positional and thematic (Congalton and Green 2002). Positional accuracy is defined as “closeness of reported coordinate values to values accepted as or being true” (Kresse and Fadaie 2004). Here, coordinate values can refer to points, lines, or two-dimensional polygons. Thematic accuracy concerns the correctness of a class (or a label) assignment. In remote sensing applications, thematic accuracy refers to the accurate measurement of the mapped land cover category at a specific location in comparison to the actual classification of these reference locations on the ground. In other words, thematic accuracy represents the accuracy of land cover classifications.
Fisher (2006) introduced a conceptual model of uncertainty in spatial data, where the class or individual objects can be described as well or poorly defined. If the objects are well defined, then the uncertainty is caused by errors and it is probabilistic in nature. If the object is poorly defined, then the definition of a class or set within the universe is a matter of vagueness or ambiguity which can be treated by using fuzzy set theory (Fisher 2006). Later, Götz et al. (2019) separated geospatial uncertainty into two categories: aleatoric and epistemic uncertainty. Aleatoric uncertainty refers to the stochastic measurement of natural variability of material properties and environmental conditions. The epistemic characteristics of uncertainty result from a lack of knowledge, which can be modeled using various approaches (e.g. intervals or fuzzy numbers). Shi (1998) believes that there are four aspects of GIS-related errors: positional, attribute, topological, and temporal. His paper focuses on addressing positional error of GIS features. The true location of a spatial feature is actually within an area somewhere around its measured location in GIS. He proposed a statistical approach to modeling the positional error of GIS featured in N-dimensions.
All the concepts of spatial uncertainty may affect thematic accuracy at different levels. If the spatial object is well defined, an error represents a difference between the true value and the observed value of data quality. An error can be caused by the imperfection of measurement equipment, environment effects, or imperfections of the observer. Thapa and Bossler (1992) classified the error into three categories: gross errors and blunders, systematic errors, and random errors. Gross errors are often caused by observers who are careless in using equipment, reading scales, and/or coding results. Systematic errors often occur in the process of computing functional relationships of data, environmental effects, instrumental imperfections, and/or human limitations. In addition to gross and systematic errors, some variations in observations will always remain. These remaining variations in observations are called random errors.
Thematic accuracy assessment is based on the selection of a sample of point locations, and a comparison of the land cover classes assigned to these locations by the classification procedure with the classes observed at these locations on a reference source. An error in positional accuracy of sample points can cause the wrong thematic classification for that location. On the other hand, traditional thematic maps have been treated as crisp sets, in which each location in the landscape is assumed to belong to single map category. Fuzzy sets-based accuracy assessment methods have been used to address the magnitude of errors and assessment of ambiguity in map classes (Woodcock and Gopal, 2000).
The accuracy of a map contains some level of uncertainty that cannot be avoided. Therefore, the question of how to ensure high-quality spatial data products is essential in defining thematic accuracy. For instance, the reference data that are assumed to be correct in thematic accuracy assessment must meet data quality criteria. On the other hand, thematic accuracy is dealing with data attribute classification, which is tightly connected with attribute and temporal accuracy in quality standard. Albrecht et al. (2018) and Batini et al. (2017) provided an overview of the relevant standards in remote sensing domain and remote sensing life cycle such as Quality Assurance Framework for Earth Observation (QA4EO; http://qa4eo.org/), which was established and endorsed by the Committee on Earth Observation Satellites (CEOS; http://ceos.org/). Here, the data quality standard plays a vital role in managing the thematic accuracy of the map since it is associated with the data quality control process of a map product.
In 1992, the Spatial Data Transfer Standard (SDTS) was approved by the National Institutes of Standards and Technology (NIST) as a Federal Information Processing Standard (FIPS) Publication, FIPS PUB 173. The U.S. Geological Survey was designated by the NIST as the agency that maintains the publication. Setting the standard allowed transferring, sharing, and integration of digital geospatial data among a diverse set of systems and sources. For example, Geography Markup Language satisfies the encoding requirements of SDTS. SDTS specified four important aspects of data quality: 1) lineage, 2) positional accuracy, 3) logical consistency, and 4) completeness and (or) logical consistency defined as follows (NSDI, 1998).
Lineage: Separate processing histories about the separate data sources should be documented.
Positional Accuracy: Existing standard (e.g., geodetic standard) shall be used to report the quality of point data. The report of any positional accuracy test shall include the date and test. A separate survey form shall also be included in the standard form, even if results fall below the recognized classification thresholds. Measures of positional accuracy may be obtained by internal evidence, deductive estimates, comparison to a source, or independent sources with higher accuracy.
Logical consistency: The quality report shall contain a description of the tests applied or a reference to documentation of the software used. The report shall describe whether all inconsistencies were corrected.
Completeness and logical consistency: Report and explain data encoding practices, especially in object records, which might be contrary to, or deviate from, normal standards and preferred practices. For example, if one or more composite object records lack lists of component objects, the meaning of this shall be explained in the completeness portion of the data quality report.
In parallel, according to the National Committee for Digital Cartographic Data Standards (NCDCDS, 1988), six fundamental components of digital cartographic data have been identified: 1) lineage 2) positional accuracy 3) logical consistency, 4) completeness 5) attribute accuracy and 6) temporal accuracy. These standards match SDTS specified four important aspects of data quality.
Lineage refers to the history of a data set. It is a description of all transformations involved in producing the final data, from its collection through the many stages of compilations, corrections, conversions, and transformations to the negation of new interpreted data products (Guptill et al., 2013).
Positional accuracy represents the degree of compliance or the nearness of those value to the entity’s “true” position in that system (Guptill et al., 2013). Description of positional accuracy must consider the quality of the final product.
Logical consistency is used to measure the fidelity of relationships encoded in the digital cartographic data structure.
The report on completeness shall describe the relationship between the spatial objects represented towards an abstract universe of such objects. The completeness accuracy test can be obtained from a topological test for logical consistency.
Attribute accuracy defines the quality of each attribute class. For instance, post classification comparisons of thematic data using the error matrix is the popular method for describing the attribute accuracy of land cover classified from remotely sensed data.
Finally, the temporal accuracy refers to the accuracy of reported time (dates in various data collection and testing steps) compared to the actual time the tasks were implemented. Table 1 illustrates examples of applying data quality criteria in thematic accuracy assessment. This table will also help people to evaluate if the produced information fulfills the quality requirements or not.
Table 1. Examples of Using Data Quality Criteria in Thematic Accuracy Assessment
Data Quality Criteria
Examples in Thematic Accuracy
Lineage
Is the documentation of input data and the classification process for the thematic map complete and allows others to repeat or reproduce the study?
Positional Accuracy
Is the map free of any positional shifts that would degrade the quality of subsequent comparisons with other information?
Attribute Accuracy
Are attributes identified on a remote sensing image, in fact, correct?
Completeness
Is the coverage of the classes complete on the remote sensing image? This refers to error of omission or commission in spatial data.
Logical Consistency
In a thematic map, do different classes have correct topological relationships? Logical consistency addresses verification of topological join relationships.
Temporal Accuracy
Is the age or timelines of a remote sensing image specified correctly in the documentation? It concerns the dates of data acquisition, types of updates and validity periods.
High-resolution remote sensing images introduced the need for quantitative methods to evaluate the accuracy of a mapped land cover category at a particular time compared to what was actually on the ground at that time. Satellite imagery is important for many applications including disaster management (Singh and Singh 2017), earth observations (Manaf et al. 2018; Crawford et al. 2013), agriculture management (Picoli et al. 2018; Herbei et al. 2016), and urban expansion assessment (Cauwels et al. 2014; Duede and Zhorin 2016). Land-cover maps are often constructed using remotely sensed data that compiles data important to map users. For instance, land cover and land use classifications from remotely sensed data are often used for mapping natural resources over relatively large areas at different time scales (Jensen 2005; Pontius and Millones 2011). Foody (2002) and Olofsson et al. (2014) provided good practices for estimating area and assessing land cover classification based on remote sensing images. The objective of thematic accuracy is to determine which map constructed from the candidate imagery dates, classification methods, or other options results in the highest accuracy. In order to perform a meaningful assessment of accuracy, land cover classifications must use reference data that are accepted to be correct under data quality criteria (Congalton 2007). The reference data are normally summarized in an error matrix and further computed into various accuracy statistics.
Stehman (1997) and Congalton and Green (2002) have illustrated a good example of creating an error matrix for land-cover classifications. Given a reference and image classification for all areas on the map, Pij is the probability that a randomly selected area is classified as category i by the image and as category j by the reference data. Equation 1 illustrates the overall proportion of area that is correctly classified when the sampling design is simple random. Lower case p is used to denote characteristics of the error matrix (e.g., individual cell probability pij) and row and column marginal proportions (pi+ and p+j respectively). Upper case P will be used to denote the overall proportion of area correctly classified (Pc), and user’s (PUi) and producer’s (PAj) accuracy.
The overall proportion of area correctly classified:
(1)
where q is equal to the number of land cover categories.
User’s accuracy for cover type i, the conditional probability that an area classified as category i by the map is classified as category i by the reference data using simple random sampling
(2)
Producer’s accuracy for cover type j, the conditional probability that an area classified as category j by the reference data is classified as category j by the map using random sampling,
(3)
An example of how to calculate overall accuracy, producer's accuracy, and user's accuracy is illustrated below (Figure 1).
Figure 1. An example of an error matrix. Source: author.
Gopal and Woodcock (1994) also proposed a fuzzy error matrix that incorporates linguistic descriptors to evaluate the land cover attributes associated with each sample location against each category in the classification scheme.
Olofsson (2014) introduced good practice recommendations to implement a probability sampling design, so that the sampling design should be chosen to achieve the priority objectives of accuracy and area estimation while also satisfying practical constraints such as cost and available sources of reference data. Stehman (2009) introduced cluster sampling methods, where spatially contiguous pixels are grouped into clusters and pixels are secondary sampling units. One potential drawback of cluster sampling is that cluster sampling may yield larger standard errors relative to an un-clustered design of the same cost if classification error is spatially autocorrelated. In this case, two-stage cluster sampling may considerably reduce costs relative to one-stage sampling while diminishing the variance inflation attributable to positive within-cluster correlation of classification error.
Spatial autocorrelation is used to measure the similarity between observations for a given variable as a function of spatial distance (Dubin 1998). The Moran’s I coefficient is the most commonly used coefficient in univariate autocorrelation analysis and is given by:
(4)
where n is the number of observations indexed by i and j. yi and yj represented the variable of interest at locations of interest in i and j, is the mean of y, and wij, where wij is an element of the matrix W. In this matrix, wij=1 if the pair i, j is within a given distance class interval, otherwise wij = 0. S indicates the sum of of all wij in the W matrix. Values of I usually range from −1 to +1. Values significantly below -1/(N-1) indicate negative spatial autocorrelation and values significantly above -1/(N-1) indicate positive spatial autocorrelation.
Spatial autocorrelation has been an important theory for observing non-stationary spatial variation. Comber et al. (2012) used geographically weighted approaches to model the non-stationary spatial variations in the accuracy of Boolean and fuzzy land cover classes.
References:
Albrecht, F., Blaschke, T., Lang, S., Abdulmutalib, H.M., Szabó, G., Barsi, Á., Batini, C., Bartsch, A., Kugler, Z., Tiede, D. and Huang, G., (2018). Providng data quality information for remote sensing applications. International Archives of the Photogrammetry, Remote Sensing & Spatial Information Sciences, 42(3).
Batini, C., Blaschke, T., Lang, S., Albrecht, F., Abdulmutalib, H.M., Barsi, Á., Szabó, G. and Kugler, Z., (2017). Data Quality in Remote Sensing. International Archives of the Photogrammetry, Remote Sensing & Spatial Information Sciences, 42.
Comber, A., Fisher, P., Brunsdon, C., and Khmag, A. (2012). Spatial analysis of remote sensing image classification accuracy. Remote Sensing of Environment, 127, 237-246. DOI: 10.1016/j.rse.2012.09.005
Crawford, C.J, Manson, S.M, Bauer, M.E, Hall, D.K. (2013). Multitemporal snow cover mapping in mountainous terrain for Landsat climate data record development. Remote Sens Environ 135:224–233
Cauwels, P., Pestalozzi, N., and Sornette, D. (2014). Dynamics and spatial distribution of global nighttime lights. EPJ Data Science, 3(1), 2.
Congalton, R. G., and Green, K. (2002). Assessing the accuracy of remotely sensed data: principles and practices. CRC press.
Congalton, R. G. (2007). Thematic and positional accuracy assessment of digital remotely sensed data. In In: McRoberts, Ronald E.; Reams, Gregory A.; Van Deusen, Paul C.; McWilliams, William H., eds. Proceedings of the seventh annual forest inventory and analysis symposium; October 3-6, 2005; Portland, ME. Gen. Tech. Rep. WO-77. Washington, DC: US Department of Agriculture, Forest Service: 149-154. (Vol. 77).
Dubin, R. A. (1998). Spatial autocorrelation: a primer. Journal of Housing Economics, 7(4), 304-327.
Duede E, Zhorin V (2016) Convergence of economic growth and the great recession as seen from a celestial observatory. EPJ Data Science 5(1):1–29
Fisher P., Comber A., and Wadsworth R., (2006). Approaches to uncertainty in spatial data. Fundamentals of spatial data quality, R. Devillers and R. Jeansoulin eds., ISTE: London, 43-59.
Foody, G. M. (2002), Status of land cover classification accuracy assessment, Remote Sensing of Environment, 80: 185-201.
Goodchild, M. F. (1992). Geographical information science. International Journal of Geographical Information Systems, 6(1), 31-45. DOI: 10.1080/02693799208901893
Gopal, S., and Woodcock, C. (1994). Theory and methods for accuracy assessment of thematic maps using fuzzy sets. Photogrammetric Engineering and Remote Sensing, 60(2),181-188.
Guptill, S.C. and Morrison, J.L. eds., 2013. Elements of spatial data quality. Elsevier.
Götz, M., Graf, W., and Kaliske, M. (2019). Enhanced uncertain structural analysis with time-and spatial-dependent (functional) fuzzy results. Mechanical Systems and Signal Processing, 119, 23-38. DOI: 10.1016/j.ymssp.2018.08.041
Herbei, M. V., Popescu, C. A., Bertici, R., Smuleac, A., & Popescu, G. (2016). Processing and Use of Satellite Images in Order to Extract Useful Information in Precision Agriculture. Bulletin of University of Agricultural Sciences and Veterinary Medicine Cluj-Napoca. Agriculture, 73(2), 238-246.
Jensen, J. R. (2005). Introductory digital image processing: a remote sensing perspective (3rd ed.). Upper Saddle River, N.J.: Prentice Hall, p. 502-5.
Kresse, W., and Fadaie, K. (2004). ISO standards for geographic information. Springer Science & Business Media.
Longley, P. A., Goodchild, M. F., Maguire, D. J., & Rhind, D. W. (2005). Geographic Information Systems and Science. John Wiley & Sons.
Manaf, S. A., Mustapha, N., Sulaiman, M., Husin, N. A., and Hamid, M. R. A. (2018). Artificial Neural Networks for Satellite Image Classification of Shoreline Extraction for Land and Water Classes of the North West Coast of Peninsular Malaysia. Advanced Science Letters, 24(2), 1382-1387.
NCDCDS, (1988). Digital Cartographic Data Quality. The American Cartographer, 15:1, 129-135.
Olofsson, P., Foody, G. M., Herold, M., Stehman, S. V., Woodcock, C. E., & Wulder, M. A. (2014). Good practices for estimating area and assessing accuracy of land change. Remote Sensing of Environment, 148, 42-57.
Pontius, R. G., & Millones, M. (2011). Death to Kappa: birth of quantity disagreement and allocation disagreement for accuracy assessment. International Journal of Remote Sensing, 32(15), 4407-4429. doi:10.1080/01431161.2011.552923
Picoli, M.C.A., Camara, G., Sanches, I., Simões, R., Carvalho, A., Maciel, A., Coutinho, A., Esquerdo, J., Antunes, J., Begotti, R.A. and Arvor, D., (2018). Big earth observation time series analysis for monitoring Brazilian agriculture. ISPRS journal of photogrammetry and remote sensing, 145, pp.328-339.
Shi, W. (1998). A generic statistical approach for modelling error of geometric features in GIS. International Journal of Geographical Information Science, 12(2), 131-143. DOI: 10.1080/136588198241923
Stehman, S. V. (1997). Selecting and interpreting measures of thematic classification accuracy. Remote sensing of Environment, 62(1), 77-89. DOI: 10.1016/S0034-4257(97)00083-7
Stehman, S. V. (2009). Sampling designs for accuracy assessment of land cover. International Journal of Remote Sensing, 30: 5243-5272.
Singh, A., & Singh, K. K. (2017). Satellite image classification using Genetic Algorithm trained radial basis function neural network, application to the detection of flooded areas. Journal of Visual Communication and Image Representation, 42, 173-182.
Thapa, K., and Bossler, J. (1992). Accuracy of spatial data used information systems. Photogrammetric Engineering and Remote Sensing, 58(6), 835-841.
Woodcock, C.E. and Gopal, S., (2000). Fuzzy set theory and thematic maps: accuracy assessment and area estimation. International Journal of Geographical Information Science, 14(2), pp.153-172.
Learning Objectives:
Explain how to perform accuracy assessment for remote sensing image classifications.
Explain what an error matrix is.
Discuss how measures of spatial autocorrelation may be used to characterize non-stationary spatial variation for thematic accuracy
Assess aspects of data quality that are described in the Spatial Data Transfer Standard.
Instructional Assessment Questions:
Provide examples on how data quality is related to the thematic accuracy.
How are measures of spatial autocorrelation related to non-stationary spatial variation?
Explain four important aspects of data quality that are described in the Spatial Data Transfer Standard.
You are currently viewing an archived version of Topic Thematic Accuracy Assessment. If updates or revisions have been published you can find them at Thematic Accuracy Assessment.
Geographic Information System (GIS) applications often involve various analytical techniques and geographic data to produce thematic maps for gaining a better understanding of geospatial situations to support spatial decisions. Accuracy assessment of a thematic map is necessary for evaluating the quality of the research results and ensuring appropriate use of the geographic data. Thematic accuracy deals with evaluating the accuracy of the attributes or labels of mapped features by comparing them to a reference that is assumed to be true. The fundamental practice presents the remote sensing approach to thematic accuracy assessment as a good guidance. For instance, the accuracy of a remote sensing image can be represented as an error matrix when the map and reference classification are conducted based on categories. This entry introduces basic concepts and techniques used in conducting thematic accuracy with an emphasis on land cover classification based on remote sensing images. The entry first introduces concepts of spatial uncertainty and spatial data quality standards and further gives an example of how spatial data quality affects thematic accuracy. Additionally, the entry illustrates the techniques that can be used to access thematic accuracy as well as using spatial autocorrelation in thematic accuracy sampling design.
Zhang, Z. (2020). Thematic Accuracy Assessment. The Geographic Information Science & Technology Body of Knowledge (2nd Quarter 2020 Edition), John P. Wilson (ed.). DOI: 10.22224/gistbok/2020.2.3.
This entry was published on June 12, 2020.
An earlier version can be found at:
DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Thematic accuracy. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital).
1. Spatial Uncertainty
Uncertainty is an inherent attribute of geographic information and knowledge representation because perfect knowledge is hard to obtain (Goodchild 1992; Longley 2005). Any collection of observational geographical information is prone to uncertainty in several forms. Generally, there are two types of map accuracy assessments: positional and thematic (Congalton and Green 2002). Positional accuracy is defined as “closeness of reported coordinate values to values accepted as or being true” (Kresse and Fadaie 2004). Here, coordinate values can refer to points, lines, or two-dimensional polygons. Thematic accuracy concerns the correctness of a class (or a label) assignment. In remote sensing applications, thematic accuracy refers to the accurate measurement of the mapped land cover category at a specific location in comparison to the actual classification of these reference locations on the ground. In other words, thematic accuracy represents the accuracy of land cover classifications.
Fisher (2006) introduced a conceptual model of uncertainty in spatial data, where the class or individual objects can be described as well or poorly defined. If the objects are well defined, then the uncertainty is caused by errors and it is probabilistic in nature. If the object is poorly defined, then the definition of a class or set within the universe is a matter of vagueness or ambiguity which can be treated by using fuzzy set theory (Fisher 2006). Later, Götz et al. (2019) separated geospatial uncertainty into two categories: aleatoric and epistemic uncertainty. Aleatoric uncertainty refers to the stochastic measurement of natural variability of material properties and environmental conditions. The epistemic characteristics of uncertainty result from a lack of knowledge, which can be modeled using various approaches (e.g. intervals or fuzzy numbers). Shi (1998) believes that there are four aspects of GIS-related errors: positional, attribute, topological, and temporal. His paper focuses on addressing positional error of GIS features. The true location of a spatial feature is actually within an area somewhere around its measured location in GIS. He proposed a statistical approach to modeling the positional error of GIS featured in N-dimensions.
All the concepts of spatial uncertainty may affect thematic accuracy at different levels. If the spatial object is well defined, an error represents a difference between the true value and the observed value of data quality. An error can be caused by the imperfection of measurement equipment, environment effects, or imperfections of the observer. Thapa and Bossler (1992) classified the error into three categories: gross errors and blunders, systematic errors, and random errors. Gross errors are often caused by observers who are careless in using equipment, reading scales, and/or coding results. Systematic errors often occur in the process of computing functional relationships of data, environmental effects, instrumental imperfections, and/or human limitations. In addition to gross and systematic errors, some variations in observations will always remain. These remaining variations in observations are called random errors.
Thematic accuracy assessment is based on the selection of a sample of point locations, and a comparison of the land cover classes assigned to these locations by the classification procedure with the classes observed at these locations on a reference source. An error in positional accuracy of sample points can cause the wrong thematic classification for that location. On the other hand, traditional thematic maps have been treated as crisp sets, in which each location in the landscape is assumed to belong to single map category. Fuzzy sets-based accuracy assessment methods have been used to address the magnitude of errors and assessment of ambiguity in map classes (Woodcock and Gopal, 2000).
2. Quality and Accuracy of Spatial Data
The accuracy of a map contains some level of uncertainty that cannot be avoided. Therefore, the question of how to ensure high-quality spatial data products is essential in defining thematic accuracy. For instance, the reference data that are assumed to be correct in thematic accuracy assessment must meet data quality criteria. On the other hand, thematic accuracy is dealing with data attribute classification, which is tightly connected with attribute and temporal accuracy in quality standard. Albrecht et al. (2018) and Batini et al. (2017) provided an overview of the relevant standards in remote sensing domain and remote sensing life cycle such as Quality Assurance Framework for Earth Observation (QA4EO; http://qa4eo.org/), which was established and endorsed by the Committee on Earth Observation Satellites (CEOS; http://ceos.org/). Here, the data quality standard plays a vital role in managing the thematic accuracy of the map since it is associated with the data quality control process of a map product.
In 1992, the Spatial Data Transfer Standard (SDTS) was approved by the National Institutes of Standards and Technology (NIST) as a Federal Information Processing Standard (FIPS) Publication, FIPS PUB 173. The U.S. Geological Survey was designated by the NIST as the agency that maintains the publication. Setting the standard allowed transferring, sharing, and integration of digital geospatial data among a diverse set of systems and sources. For example, Geography Markup Language satisfies the encoding requirements of SDTS. SDTS specified four important aspects of data quality: 1) lineage, 2) positional accuracy, 3) logical consistency, and 4) completeness and (or) logical consistency defined as follows (NSDI, 1998).
In parallel, according to the National Committee for Digital Cartographic Data Standards (NCDCDS, 1988), six fundamental components of digital cartographic data have been identified: 1) lineage 2) positional accuracy 3) logical consistency, 4) completeness 5) attribute accuracy and 6) temporal accuracy. These standards match SDTS specified four important aspects of data quality.
Table 1. Examples of Using Data Quality Criteria in Thematic Accuracy Assessment
Is the age or timelines of a remote sensing image specified correctly in the documentation? It concerns the dates of data acquisition, types of updates and validity periods.
3. Thematic Accuracy
High-resolution remote sensing images introduced the need for quantitative methods to evaluate the accuracy of a mapped land cover category at a particular time compared to what was actually on the ground at that time. Satellite imagery is important for many applications including disaster management (Singh and Singh 2017), earth observations (Manaf et al. 2018; Crawford et al. 2013), agriculture management (Picoli et al. 2018; Herbei et al. 2016), and urban expansion assessment (Cauwels et al. 2014; Duede and Zhorin 2016). Land-cover maps are often constructed using remotely sensed data that compiles data important to map users. For instance, land cover and land use classifications from remotely sensed data are often used for mapping natural resources over relatively large areas at different time scales (Jensen 2005; Pontius and Millones 2011). Foody (2002) and Olofsson et al. (2014) provided good practices for estimating area and assessing land cover classification based on remote sensing images. The objective of thematic accuracy is to determine which map constructed from the candidate imagery dates, classification methods, or other options results in the highest accuracy. In order to perform a meaningful assessment of accuracy, land cover classifications must use reference data that are accepted to be correct under data quality criteria (Congalton 2007). The reference data are normally summarized in an error matrix and further computed into various accuracy statistics.
Stehman (1997) and Congalton and Green (2002) have illustrated a good example of creating an error matrix for land-cover classifications. Given a reference and image classification for all areas on the map, Pij is the probability that a randomly selected area is classified as category i by the image and as category j by the reference data. Equation 1 illustrates the overall proportion of area that is correctly classified when the sampling design is simple random. Lower case p is used to denote characteristics of the error matrix (e.g., individual cell probability pij) and row and column marginal proportions (pi+ and p+j respectively). Upper case P will be used to denote the overall proportion of area correctly classified (Pc), and user’s (PUi) and producer’s (PAj) accuracy.
The overall proportion of area correctly classified:
where q is equal to the number of land cover categories.
User’s accuracy for cover type i, the conditional probability that an area classified as category i by the map is classified as category i by the reference data using simple random sampling
Producer’s accuracy for cover type j, the conditional probability that an area classified as category j by the reference data is classified as category j by the map using random sampling,
An example of how to calculate overall accuracy, producer's accuracy, and user's accuracy is illustrated below (Figure 1).
Figure 1. An example of an error matrix. Source: author.
Gopal and Woodcock (1994) also proposed a fuzzy error matrix that incorporates linguistic descriptors to evaluate the land cover attributes associated with each sample location against each category in the classification scheme.
Olofsson (2014) introduced good practice recommendations to implement a probability sampling design, so that the sampling design should be chosen to achieve the priority objectives of accuracy and area estimation while also satisfying practical constraints such as cost and available sources of reference data. Stehman (2009) introduced cluster sampling methods, where spatially contiguous pixels are grouped into clusters and pixels are secondary sampling units. One potential drawback of cluster sampling is that cluster sampling may yield larger standard errors relative to an un-clustered design of the same cost if classification error is spatially autocorrelated. In this case, two-stage cluster sampling may considerably reduce costs relative to one-stage sampling while diminishing the variance inflation attributable to positive within-cluster correlation of classification error.
4. Spatial Autocorrelation and Non-Stationarity of Spatial Variation
Spatial autocorrelation is used to measure the similarity between observations for a given variable as a function of spatial distance (Dubin 1998). The Moran’s I coefficient is the most commonly used coefficient in univariate autocorrelation analysis and is given by:
where n is the number of observations indexed by i and j. yi and yj represented the variable of interest at locations of interest in i and j,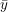 is the mean of y, and wij, where wij is an element of the matrix W. In this matrix, wij=1 if the pair i, j is within a given distance class interval, otherwise wij = 0. S indicates the sum of of all wij in the W matrix. Values of I usually range from −1 to +1. Values significantly below -1/(N-1) indicate negative spatial autocorrelation and values significantly above -1/(N-1) indicate positive spatial autocorrelation.
is the mean of y, and wij, where wij is an element of the matrix W. In this matrix, wij=1 if the pair i, j is within a given distance class interval, otherwise wij = 0. S indicates the sum of of all wij in the W matrix. Values of I usually range from −1 to +1. Values significantly below -1/(N-1) indicate negative spatial autocorrelation and values significantly above -1/(N-1) indicate positive spatial autocorrelation.
Spatial autocorrelation has been an important theory for observing non-stationary spatial variation. Comber et al. (2012) used geographically weighted approaches to model the non-stationary spatial variations in the accuracy of Boolean and fuzzy land cover classes.
Albrecht, F., Blaschke, T., Lang, S., Abdulmutalib, H.M., Szabó, G., Barsi, Á., Batini, C., Bartsch, A., Kugler, Z., Tiede, D. and Huang, G., (2018). Providng data quality information for remote sensing applications. International Archives of the Photogrammetry, Remote Sensing & Spatial Information Sciences, 42(3).
Batini, C., Blaschke, T., Lang, S., Albrecht, F., Abdulmutalib, H.M., Barsi, Á., Szabó, G. and Kugler, Z., (2017). Data Quality in Remote Sensing. International Archives of the Photogrammetry, Remote Sensing & Spatial Information Sciences, 42.
Comber, A., Fisher, P., Brunsdon, C., and Khmag, A. (2012). Spatial analysis of remote sensing image classification accuracy. Remote Sensing of Environment, 127, 237-246. DOI: 10.1016/j.rse.2012.09.005
Crawford, C.J, Manson, S.M, Bauer, M.E, Hall, D.K. (2013). Multitemporal snow cover mapping in mountainous terrain for Landsat climate data record development. Remote Sens Environ 135:224–233
Cauwels, P., Pestalozzi, N., and Sornette, D. (2014). Dynamics and spatial distribution of global nighttime lights. EPJ Data Science, 3(1), 2.
Congalton, R. G., and Green, K. (2002). Assessing the accuracy of remotely sensed data: principles and practices. CRC press.
Congalton, R. G. (2007). Thematic and positional accuracy assessment of digital remotely sensed data. In In: McRoberts, Ronald E.; Reams, Gregory A.; Van Deusen, Paul C.; McWilliams, William H., eds. Proceedings of the seventh annual forest inventory and analysis symposium; October 3-6, 2005; Portland, ME. Gen. Tech. Rep. WO-77. Washington, DC: US Department of Agriculture, Forest Service: 149-154. (Vol. 77).
Dubin, R. A. (1998). Spatial autocorrelation: a primer. Journal of Housing Economics, 7(4), 304-327.
Duede E, Zhorin V (2016) Convergence of economic growth and the great recession as seen from a celestial observatory. EPJ Data Science 5(1):1–29
Fisher P., Comber A., and Wadsworth R., (2006). Approaches to uncertainty in spatial data. Fundamentals of spatial data quality, R. Devillers and R. Jeansoulin eds., ISTE: London, 43-59.
Foody, G. M. (2002), Status of land cover classification accuracy assessment, Remote Sensing of Environment, 80: 185-201.
Goodchild, M. F. (1992). Geographical information science. International Journal of Geographical Information Systems, 6(1), 31-45. DOI: 10.1080/02693799208901893
Gopal, S., and Woodcock, C. (1994). Theory and methods for accuracy assessment of thematic maps using fuzzy sets. Photogrammetric Engineering and Remote Sensing, 60(2),181-188.
Guptill, S.C. and Morrison, J.L. eds., 2013. Elements of spatial data quality. Elsevier.
Götz, M., Graf, W., and Kaliske, M. (2019). Enhanced uncertain structural analysis with time-and spatial-dependent (functional) fuzzy results. Mechanical Systems and Signal Processing, 119, 23-38. DOI: 10.1016/j.ymssp.2018.08.041
Herbei, M. V., Popescu, C. A., Bertici, R., Smuleac, A., & Popescu, G. (2016). Processing and Use of Satellite Images in Order to Extract Useful Information in Precision Agriculture. Bulletin of University of Agricultural Sciences and Veterinary Medicine Cluj-Napoca. Agriculture, 73(2), 238-246.
Jensen, J. R. (2005). Introductory digital image processing: a remote sensing perspective (3rd ed.). Upper Saddle River, N.J.: Prentice Hall, p. 502-5.
Kresse, W., and Fadaie, K. (2004). ISO standards for geographic information. Springer Science & Business Media.
Longley, P. A., Goodchild, M. F., Maguire, D. J., & Rhind, D. W. (2005). Geographic Information Systems and Science. John Wiley & Sons.
Manaf, S. A., Mustapha, N., Sulaiman, M., Husin, N. A., and Hamid, M. R. A. (2018). Artificial Neural Networks for Satellite Image Classification of Shoreline Extraction for Land and Water Classes of the North West Coast of Peninsular Malaysia. Advanced Science Letters, 24(2), 1382-1387.
NCDCDS, (1988). Digital Cartographic Data Quality. The American Cartographer, 15:1, 129-135.
NSDI, (1998). Spatial data transfer standard (SDTS) part 6: Point Profile. Available from web: https://www.ngs.noaa.gov/FGCS/tech_pub/sdtsp.html (Accessed 09.27.2019)
Olofsson, P., Foody, G. M., Herold, M., Stehman, S. V., Woodcock, C. E., & Wulder, M. A. (2014). Good practices for estimating area and assessing accuracy of land change. Remote Sensing of Environment, 148, 42-57.
Pontius, R. G., & Millones, M. (2011). Death to Kappa: birth of quantity disagreement and allocation disagreement for accuracy assessment. International Journal of Remote Sensing, 32(15), 4407-4429. doi:10.1080/01431161.2011.552923
Picoli, M.C.A., Camara, G., Sanches, I., Simões, R., Carvalho, A., Maciel, A., Coutinho, A., Esquerdo, J., Antunes, J., Begotti, R.A. and Arvor, D., (2018). Big earth observation time series analysis for monitoring Brazilian agriculture. ISPRS journal of photogrammetry and remote sensing, 145, pp.328-339.
Shi, W. (1998). A generic statistical approach for modelling error of geometric features in GIS. International Journal of Geographical Information Science, 12(2), 131-143. DOI: 10.1080/136588198241923
Stehman, S. V. (1997). Selecting and interpreting measures of thematic classification accuracy. Remote sensing of Environment, 62(1), 77-89. DOI: 10.1016/S0034-4257(97)00083-7
Stehman, S. V. (2009). Sampling designs for accuracy assessment of land cover. International Journal of Remote Sensing, 30: 5243-5272.
Singh, A., & Singh, K. K. (2017). Satellite image classification using Genetic Algorithm trained radial basis function neural network, application to the detection of flooded areas. Journal of Visual Communication and Image Representation, 42, 173-182.
Thapa, K., and Bossler, J. (1992). Accuracy of spatial data used information systems. Photogrammetric Engineering and Remote Sensing, 58(6), 835-841.
Woodcock, C.E. and Gopal, S., (2000). Fuzzy set theory and thematic maps: accuracy assessment and area estimation. International Journal of Geographical Information Science, 14(2), pp.153-172.
Keywords: