AM-17 - Intervisibility, Line-of-Sight, and Viewsheds
You are currently viewing an archived version of Topic Intervisibility, Line-of-Sight, and Viewsheds.
If updates or revisions have been published you can find them at Intervisibility, Line-of-Sight, and Viewsheds.
The visibility of a place refers to whether it can be seen by observers from one or multiple other locations. Modeling the visibility of points has various applications in GIS, such as placement of observation points, military observation, line-of-sight communication, optimal path route planning, and urban design. This chapter provides a brief introduction to visibility analysis, including an overview of basic conceptions in visibility analysis, the methods for computing intervisibility using discrete and continuous approaches based on DEM and TINs, the process of intervisibility analysis, viewshed and reverse viewshed analysis. Several practical applications involving visibility analysis are illustrated for geographical problem-solving. Finally, existing software and toolboxes for visibility analysis are introduced.
Author and Citation Info:
Kang, Y. (2022). Intervisibility, Line-of-Sight, and Viewsheds. The Geographic Information Science & Technology Body of Knowledge (2nd Quarter 2022 Edition). John P. Wilson (Ed.). DOI: https://doi.org/10.22224/gistbok/2022.2.8.
This Topic is also available in the following editions: DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Intervisibility. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital)
Acknowledgements: Some content was adopted from Prof. A-Xing Zhu’s course material with permission: Geography 579, Spatial Analysis, University of Wisconsin-Madison.
Digital Elevation Model (DEM): a three-dimensional representation of data to represent a terrain’s surface (topography) based on a regularly spaced rectangular grid, and is used as the generic term for DSMs (Digital Surface Models) and DTMs (Digital Terrain Models).
Elevation: the height or depth of a terrain element with respect to a vertical datum plane such as sea level.
Intervisibility analysis: solve visibility between two or more viewpoints.
Line-of-sight: the visual connections between two points (from observer to target point).
Network: a network is a graph that is made up of nodes (may refer to geographic entities as vertices) and connected by edges (may refer to links). It can be used to represent spatial relationships of adjacent geographic objects, such as constructing TINs.
Raster: a regularly spaced, grid-like data model to record, analyze, and visualize data with a continuous nature. The basic element is referred to as a cell, pixel, or grid point.
Raster cell: a raster cell is the basic unit of the raster data that stores a single value to represent a specific attribute.
Reverse viewshed analysis: determination of area (or places) from which the target point can be visible.
Surface: the outermost part of the water or land and all objects on it.
Terrain: the vertical and horizontal dimensions of the land surface.
Triangulated Irregular Networks (TINs): a representation of a continuous surface based on triangular facets used mainly for elevation modeling.
Viewpoint: a position from which people can observe other places.
Viewshed analysis: calculate the area that is visible from a given point.
Visibility analysis serves as a critical part of human-environment interaction studies and a fundamental feature of Geographic Information Systems (Inglis et al., 2022), and has been used in a wide range of applications such as urban design assessment, military observation, optimal path route planning, archeological site analysis, placement of viewpoint, and tree cover conservation (Nagy, 1994). Visibility analysis aims at examining whether a place can be seen by observers from other locations. It consists of two types of analysis: intervisibility analysis, which predicts whether one location or termed a viewpoint, is visible from another; and viewshed analysis, which determines the entire area that could be seen from a given viewpoint (Kim et al., 2004). To conduct the visibility analysis, the elevation of the terrain as well as observer information are used to infer the line-of-sight. Visibility analysis may take into account several factors that influence terrain visibility, such as vegetation cover (Llobera, 2007). While other relevant factors such as weather conditions and time of day may be overlooked so that visibility analysis is performed based on the assumption of ideal conditions (Rua et al., 2013). As shown in Figure 1, two line-of-sights are constructed from observer point A, and observer point B to the target viewpoint on the terrain surface. From observer point A, the target point is not visible as the line-of-sight is blocked by topography (indicated by the red dash line). While the line-of-sight connects the observer point B and the target point, indicating that the target point is visible from the observer point B.
Figure 1. An example of visibility analysis: the target point can be seen from the observer point B while is invisible from the observer point A. Source: author.
In general, the elevations of input points can be taken either from the raster-based Digital Elevation Model (DEM) or vector-based triangulated irregular networks (TINs). Both kinds of models are used for representing the topographic surface (or terrain). There are two types of approaches in terms of modeling the intervisibility of a certain viewpoint, namely, discrete and continuous intervisibility approaches (De Floriani & Magillo, 1999; Floriani & Magillo, 2003). Discrete approaches are appropriate for mapping the intervisibility of DEM, while continuous intervisibility approaches are usually used for TINs. Given the diverse data structures of DEM and TINs, the methods for conducting visibility analysis of these two forms of data are different and are summarized in the following subsections. It should be noted that there are no clear distinctions between the two categories of approaches. For example, the continuous intervisibility approach might be used for computing visibility analysis based on DEMs data as well.
2.1 Discrete Intervisibility Approach based on Line-of-sight
The core part of the visibility analysis with the raster-based DEM data refers to the inference of line-of-sight. Given certain terrain conditions, the line-of-sight indicates whether the targeting viewpoint can be seen from the observer viewpoint. In other words, it determines if there is a location whose elevation will block the sightline between the two DEM cells (i.e., observer cell and target cell). The target point is included in the viewshed if the line of sight is visible; while if the line of sight is obscured, the target point is not included in the viewshed. The computational process is illustrated as follows.
Figure 2. Abstraction of Line-of-Sight Computation. Source: author.
As is shown in Figure 2, points Pobserver and Ptarget designate the observer and the target point, respectively. PointPx refers to a given point in the study area. The elevations of the observer and the target points are represented by Hobserver and Htarget. Hx defines the height of the place Px. Dox denotes the horizontal distance between the observer Pobserver and Px, and Dxt represents the distance between Px and the target Ptarget. Hx is the highest elevation of the point Px that does not block the sight line between the observer and the target viewpoint.
The following equation is used to compute:
(Equation 1)
If a target location can be seen from the distant observer point, the following condition must be met:
For the elevation Hx of any location between the two viewpoints Pobserver and Ptarget: (Equation 2)
Considering the size of the grid, the computation of intervisibility using discrete approaches often requires expensive computing resources, which can be accelerated by using parallel algorithms to take advantage of the spatial structure of raster data.
2.2 Continuous Intervisibility Approach
Computational geometry algorithms are employed for calculating the intervisibility of continuous data structures such as TINs where terrains are described as polyhedral surfaces. The strategy used to solve the hidden surface removal (HSR) problem for a 3-dimensional scene is adopted as a continuous intervisibility approach (De Floriani, 1989). Specifically, the visible image of a scene is created by: (1) projecting each face of the terrain surface from the viewpoint, (2) only the visible portions of each face of the scene are maintained using the HSR algorithm.
Figure 3. The visible image of the surfaces. Source: author.
2.3 Intervisibility
Intervisibility analysis determines whether a specific observer point or an object at the observer point can be seen from another viewpoint. For DEM data using the discrete approach, a Boolean value is computed based on whether the line-of-sight is blocked or not. While using the continuous approach for TINs, the visible and invisible areas of the observer point will be partitioned, and where the target viewpoint locate will be examined. An example is illustrated in Figure 4 where a line-of-sight is constructed from the observer point to the target point. The green line indicates the visible part of the line-of-sight, and the red line indicates the invisible part of the line-of-sight. The target point cannot be seen from the observer point as shown in Figure 4 as the line-of-sight is blocked by buildings. It should be noted that intervisibility analysis can be conducted between multiple observer and target viewpoints. However, the computational process is still based on the examination of the visibility relationship between two specified points (i.e., an observer point and a specific target point).
Figure 4. An example of intervisibility between an observer point and a target group. Image source: author, with data from West Virginia View.
2.4 Viewshed Analysis
A viewshed identifies the entire area in the study area that can be observed from one or more viewpoints. To find the viewshed of a specific observation point based on DEM data, the line-of-sights between the observer point and all other cells are computed. The viewshed map is thus represented as an array of Boolean values to indicate whether each grid cell or pixel is visible or invisible. For TINs data, the viewshed can be obtained by overlaying the visibility maps of each terrain face.
Figure 5. An example of a visibility map. Source: author.
Figure 5 shows an example of output for viewshed analysis. The left figure shows the terrain surfaces. One observer point is shown as a gold star, and two target points are shown as gold triangles. In the right figure, the visible area from the observer viewpoint is shown in green, and the invisible area in the output raster is shown in red. Two line-of-sights are constructed between the observer point and target points. Only one target point can be seen from the observer point as indicated by the green line. By assessing the visibility of each location on terrain surfaces from the observer point, the viewshed area can be constructed.
2.5 Reverse Viewshed Analysis
On the other hand, reverse viewshed analysis is utilized to identify the visibility of a given target point from many observer points, i.e., to find the area from which the target viewpoint can be seen (Fisher, 1996). The reverse viewshed analysis, in general, follows the same computing principles as the viewshed analysis to determine whether the line-of-sight between the observer and target points is blocked. However, because the heights of the viewing point and targeting objects may differ from those in the viewshed analysis (even though they may locate at the same position), the results might be different. In addition, it should be acknowledged that the outputs of reverse viewshed analysis are represented as polygons, similar to the viewshed area that contains a set of observer points.
In this section, several applications will be illustrated to show how visibility analysis can be used in solving real-world geographical problems. Traditionally, the applications for visibility analysis on terrains can be classified into the following three major categories (De Floriani & Magillo, 1999):
Placement of observation point problems.
Line-of-sight communication problems.
Visible path computation problems.
In addition to these three traditional types of applications, several recent use cases such as location accuracy assessment, interactive intervisibility analysis in 3D space, and viewshed analysis on hexagon are introduced in this section.
3.1 Placement of Observation Point Problems
Placement of observation point problems is defined as finding the optimal locations for observation points so that as much of the terrain surface within the study area as possible is visible from at least one viewpoint. The goal of this problem is to either reduce the number of viewpoints to a minimum that covers the target area or to select a fixed number of points and maximize the visible area. For instance, in addition to the existing observer point, adding which candidate observation place would maximize the viewshed area from all viewpoints, as illustrated in Figure 6. Such a problem is relevant to the p-median and p-center problems in spatial optimization. Visibility analysis has been used for locating fire towers, water towers, radar sites, and other applications.
Figure 6. An example of placement of observation point problems. Source: author.
3.2 Line-of-Sight Communication Problems
Finding the minimum number of viewpoints in the construction of a visibility network is referred to as the line-of-sight communication problem (De Floriani et al., 1994). The nodes in this visibility network correspond to observer locations, and the edges indicate the line-of-sights that connect any two consecutive viewpoints. As a result, any two consecutive viewpoints in such a network can be observed from each other. As shown in Figure 7, nearby wireless towers are connected by line-of-sights so that all three wireless towers are linked together. The solution to this problem could be used to build telephone, television, and digital data base stations.
Figure 7. An example of line-of-sight communication problems. Source: author.
3.3 Visible Path Computation Problems
The visible path computation problem refers to route planning considering visibility characteristics in terrains. Given two points (starting and destination point) and one or multiple observation points, the shortest path between the starting point and the destination point is considered a route. In practice, two types of paths are frequently computed when taking visibility qualities into account for route planning: smuggler’s paths and scenic paths. A smuggler’s path refers to a route with no points visible from observation points. On the contrary, a scenic path indicates a path in which all points are visible from the observation points (Lee & Stucky, 1998). The solution of the visible path computation problem has been widely used in several domains such as civil engineering, military activities (e.g., concealed passageways), and tourism route planning.
3.4 Location Accuracy Assessment Problems
In the era of big data, crowdsourcing volunteered geographic information (VGI) has provided a large volume of geospatial data. The quality of VGI data such as location accuracy, data bias, and representativeness, serve as fundamental issues of its usage. Recently, several studies have employed visibility analysis to assess location accuracy. For example, Senaratne et al., (2013) and Kang et al., (2018) used reverse viewshed analysis to examine whether the geotags of photos are correct by investigating if the location of photos falls within the viewshed of the observer viewpoint. Photos taken nearby Eiffel Tower are collected and mapped in Figure 8. According to the reverse viewshed analysis, green dots indicate that people at viewpoints can see the Eiffel Tower, while red dots indicate those photos cannot observe the Eiffel Tower, and their locations may not be trusted.
Figure 8. An example of reverse viewshed analysis result for location correctness checking. Source: author.
3.5 Interactive Intervisibility Analysis in 3D Space
In addition to traditional static intervisibility analysis, researchers can perform dynamic real-time interactive intervisibility analysis in 3D spaces. ArcGIS Pro provides exploratory analysis tools in which users can customize line-of-sights and viewshed by interactively creating them in real-time. As shown in Figure 9, users can create an observer point by clicking on a specific place on terrain (here it refers to buildings). The viewshed along a pre-defined direction will be generated automatically. Users can also customize the parameters of the viewshed analysis such as minimum distance, maximum distance, and direction. Such a tool enables users to have real-time visual feedback in the simulated space.
Figure 9. An example of interactive viewshed analysis in 3d space. Image source: author, with data from West Virginia View.
3.6 Integration with Hexagons, Higher Resolution Imagery, and UAV Imagery
The emergence of several new data sources and models provides new opportunities for intervisibility analysis, and they can be integrated to benefit future applications.
In addition to performing viewshed analysis on raster data based on rectangular or square raster cells, researchers have attempted to calculate viewshed on hexagonal grids (Qiang et al., 2019). To accomplish this, a binary visibility raster map is produced at first, which indicates the visibility of DEMs based on traditional rectangular raster cells. The proportion of a human observer’s viewing angle in a hexagon grid is then computed and multiplied by the viewshed raster map. Finally, the visibility of each hexagon gird is computed by summing up all intersected raster cells. Though traditional grid-based raster data remained important in the analysis, the integration of viewshed analysis with the increasingly popular hexagonal data provides valuable insights for future intervisibility-related studies with more data models.
Also, researchers have utilized higher resolution imagery from remote sensing imagery and unmanned aerial vehicles (UAVs) for modeling terrain surfaces. Such fine-resolution models bring both opportunities and challenges for intervisibility analysis. On the one hand, more fine-grained and precise intervisibility analysis can be performed to provide more accurate assessments and descriptions of viewshed on terrain surfaces. On the other hand, more computational resources are needed for obtaining the results.
Visibility analysis is an important component of existing GIS software. GIS software such as ArcGIS, QGIS, GRASS GIS, SAGA GIS, and GDAL, have provided visibility analysis tools for users to complete viewshed-related tasks.
Users can utilize visibility analysis functions based on Spatial Analyst Toolbox and 3D Analyst Toolbox in ArcGIS Pro and ArcMap for viewshed analysis provided by the ArcGIS family of products. TINs and DEM data are supported by these toolboxes. These ArcToolboxes offer a variety of visibility analysis functions including examining intervisibility, generating line of sight and viewsheds. ArcGIS Pro also provides a set of interactive exploratory analysis tools, as mentioned in section 3.5, that allows users to determine the 3D view of the viewshed and light-of-sight from a given observer point, as shown in Figure 4 and Figure 9. The viewshed and light-of-sight can be generated automatically by interactively moving the observer point. In addition, ArcGIS Online offers a “Create Viewshed” feature that allows users to perform viewshed analysis in WebGIS environments.
QGIS provides a Visibility Analysis Plugin that allows users to compute viewshed and examine the visibility of viewpoints (Cuckovic, 2016). More specifically, it provides the following functions including viewshed calculation, intervisibility network calculation, and visibility index. In comparison with ArcGIS, it only supports raster-based elevation data.
In GRASS GIS, the module r.viewshed can be used to determine the viewshed of a point based on a raster DEM. A raster map that indicates the visibility of each cell is produced given an elevation raster and the location of observer points. One unique feature of this algorithm is its optimization of the CPU usage and memory in accelerating the computing process of viewshed analysis. Consequently, r.viewshed is appropriate to compute viewshed even with very large rasters.
SAGA GIS provides the Visibility module for visibility analysis using point vector data and grid data that denotes the elevation of the terrain surface. The output visibility map of this function includes a raster layer that indicates the visibility of each grid cell.
Similarly, GDAL also provides a function gdal_viewshed to calculate the viewshed based on an input raster DEM and a user-defined point. A binary visibility raster will be generated to indicate the visibility of terrains.
In summary, all software and packages abovementioned offer the function to compute viewshed based on observation points and terrain raster layers. More functions are available in the ArcGIS family products and QGIS for more comprehensive visibility analysis.
References:
Cuckovic, Z. (2016). Advanced viewshed analysis: A Quantum GIS plug-in for the analysis of visual landscapes. The Journal of Open Source Software, 1, 32. https://doi.org/10.21105/joss.00032
De Floriani, L. (1989). A pyramidal data structure for triangle-based surface description. IEEE Computer Graphics and Applications, 9(2), 67–78. https://doi.org/10.1109/38.19053
De Floriani, L., & Magillo, P. (1999). Intervisibility on terrains. Geographic Information Systems: Principles, Techniques, Managament and Applications, 543–556.
De Floriani, L., Marzano, P., & Puppo, E. (1994). Line-of-sight communication on terrain models. International Journal of Geographical Information Systems, 8(4), 329–342. https://doi.org/10.1080/02693799408902004
Fisher, P. F. (1996). Extending the applicability of viewsheds in landscape planning. Photogrammetric Engineering and Remote Sensing, 62(11), 1297–1302.
Floriani, L., & Magillo, P. (2003). Algorithms for Visibility Computation on Terrains: A Survey. Environment and Planning B: Planning and Design, 30(5), 709–728. https://doi.org/10.1068/b12979
Inglis, N. C., Vukomanovic, J., Costanza, J., & Singh, K. K. (2022). From viewsheds to viewscapes: Trends in landscape visibility and visual quality research. Landscape and Urban Planning, 224, 104424. https://doi.org/10.1016/j.landurbplan.2022.104424
Kang, Y., Gao, S., & Liang, Y. (2018). Utilizing Reverse Viewshed Analysis in Image Geo-Localization. Proceedings of the 2nd ACM SIGSPATIAL Workshop on Recommendations for Location-Based Services and Social Networks, 1–5. https://doi.org/10.1145/3282825.3282828
Kim, Y.-H., Rana, S., & Wise, S. (2004). Exploring multiple viewshed analysis using terrain features and optimisation techniques. Computers & Geosciences, 30(9–10), 1019–1032. https://doi.org/10.1016/j.cageo.2004.07.008
Llobera, M. (2007). Modeling visibility through vegetation. International Journal of Geographical Information Science, 21(7), 799–810. https://doi.org/10.1080/13658810601169865
Qiang, Y., Shen, S., & Chen, Q. (2019). Visibility analysis of oceanic blue space using digital elevation models. Landscape and Urban Planning, 181, 92–102. https://doi.org/10.1016/j.landurbplan.2018.09.019
Rua, H., Gonçalves, A. B., & Figueiredo, R. (2013). Assessment of the Lines of Torres Vedras defensive system with visibility analysis. Journal of Archaeological Science, 40(4), 2113–2123. https://doi.org/10.1016/j.jas.2012.12.012
Senaratne, H., Bröring, A., & Schreck, T. (2013). Using Reverse Viewshed Analysis to Assess the Location Correctness of Visually Generated VGI: Assessing the Location Correctness of Visually Generated VGI. Transactions in GIS, 17(3), 369–386. https://doi.org/10.1111/tgis.12039
Learning Objectives:
Describe the general procedure of line-of-sight generation.
Describe the general procedure of viewshed computation.
Compare the discrete and continuous approaches for computing the intervisibility of viewpoints.
Describe the applications of visibility analysis.
Discuss the applications of visibility analysis in solving geographical problems.
Instructional Assessment Questions:
What are line-of-sight, viewshed, and reverse viewshed analysis?
What are the procedures for computing the intervisibility of viewpoints using discrete and continuous approaches?
Compare the viewshed analysis and reverse viewshed analysis.
Discuss the applications in viewshed analysis and demonstrate them with real-world scenarios.
You are currently viewing an archived version of Topic Intervisibility, Line-of-Sight, and Viewsheds. If updates or revisions have been published you can find them at Intervisibility, Line-of-Sight, and Viewsheds.
The visibility of a place refers to whether it can be seen by observers from one or multiple other locations. Modeling the visibility of points has various applications in GIS, such as placement of observation points, military observation, line-of-sight communication, optimal path route planning, and urban design. This chapter provides a brief introduction to visibility analysis, including an overview of basic conceptions in visibility analysis, the methods for computing intervisibility using discrete and continuous approaches based on DEM and TINs, the process of intervisibility analysis, viewshed and reverse viewshed analysis. Several practical applications involving visibility analysis are illustrated for geographical problem-solving. Finally, existing software and toolboxes for visibility analysis are introduced.
Kang, Y. (2022). Intervisibility, Line-of-Sight, and Viewsheds. The Geographic Information Science & Technology Body of Knowledge (2nd Quarter 2022 Edition). John P. Wilson (Ed.). DOI: https://doi.org/10.22224/gistbok/2022.2.8.
This Topic is also available in the following editions: DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Intervisibility. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital)
Acknowledgements: Some content was adopted from Prof. A-Xing Zhu’s course material with permission: Geography 579, Spatial Analysis, University of Wisconsin-Madison.
1. Definitions
Digital Elevation Model (DEM): a three-dimensional representation of data to represent a terrain’s surface (topography) based on a regularly spaced rectangular grid, and is used as the generic term for DSMs (Digital Surface Models) and DTMs (Digital Terrain Models).
Elevation: the height or depth of a terrain element with respect to a vertical datum plane such as sea level.
Intervisibility analysis: solve visibility between two or more viewpoints.
Line-of-sight: the visual connections between two points (from observer to target point).
Network: a network is a graph that is made up of nodes (may refer to geographic entities as vertices) and connected by edges (may refer to links). It can be used to represent spatial relationships of adjacent geographic objects, such as constructing TINs.
Raster: a regularly spaced, grid-like data model to record, analyze, and visualize data with a continuous nature. The basic element is referred to as a cell, pixel, or grid point.
Raster cell: a raster cell is the basic unit of the raster data that stores a single value to represent a specific attribute.
Reverse viewshed analysis: determination of area (or places) from which the target point can be visible.
Surface: the outermost part of the water or land and all objects on it.
Terrain: the vertical and horizontal dimensions of the land surface.
Triangulated Irregular Networks (TINs): a representation of a continuous surface based on triangular facets used mainly for elevation modeling.
Viewpoint: a position from which people can observe other places.
Viewshed analysis: calculate the area that is visible from a given point.
2. Visibility Analysis
Visibility analysis serves as a critical part of human-environment interaction studies and a fundamental feature of Geographic Information Systems (Inglis et al., 2022), and has been used in a wide range of applications such as urban design assessment, military observation, optimal path route planning, archeological site analysis, placement of viewpoint, and tree cover conservation (Nagy, 1994). Visibility analysis aims at examining whether a place can be seen by observers from other locations. It consists of two types of analysis: intervisibility analysis, which predicts whether one location or termed a viewpoint, is visible from another; and viewshed analysis, which determines the entire area that could be seen from a given viewpoint (Kim et al., 2004). To conduct the visibility analysis, the elevation of the terrain as well as observer information are used to infer the line-of-sight. Visibility analysis may take into account several factors that influence terrain visibility, such as vegetation cover (Llobera, 2007). While other relevant factors such as weather conditions and time of day may be overlooked so that visibility analysis is performed based on the assumption of ideal conditions (Rua et al., 2013). As shown in Figure 1, two line-of-sights are constructed from observer point A, and observer point B to the target viewpoint on the terrain surface. From observer point A, the target point is not visible as the line-of-sight is blocked by topography (indicated by the red dash line). While the line-of-sight connects the observer point B and the target point, indicating that the target point is visible from the observer point B.
Figure 1. An example of visibility analysis: the target point can be seen from the observer point B while is invisible from the observer point A. Source: author.
In general, the elevations of input points can be taken either from the raster-based Digital Elevation Model (DEM) or vector-based triangulated irregular networks (TINs). Both kinds of models are used for representing the topographic surface (or terrain). There are two types of approaches in terms of modeling the intervisibility of a certain viewpoint, namely, discrete and continuous intervisibility approaches (De Floriani & Magillo, 1999; Floriani & Magillo, 2003). Discrete approaches are appropriate for mapping the intervisibility of DEM, while continuous intervisibility approaches are usually used for TINs. Given the diverse data structures of DEM and TINs, the methods for conducting visibility analysis of these two forms of data are different and are summarized in the following subsections. It should be noted that there are no clear distinctions between the two categories of approaches. For example, the continuous intervisibility approach might be used for computing visibility analysis based on DEMs data as well.
2.1 Discrete Intervisibility Approach based on Line-of-sight
The core part of the visibility analysis with the raster-based DEM data refers to the inference of line-of-sight. Given certain terrain conditions, the line-of-sight indicates whether the targeting viewpoint can be seen from the observer viewpoint. In other words, it determines if there is a location whose elevation will block the sightline between the two DEM cells (i.e., observer cell and target cell). The target point is included in the viewshed if the line of sight is visible; while if the line of sight is obscured, the target point is not included in the viewshed. The computational process is illustrated as follows.
Figure 2. Abstraction of Line-of-Sight Computation. Source: author.
As is shown in Figure 2, points Pobserver and Ptarget designate the observer and the target point, respectively. Point Px refers to a given point in the study area. The elevations of the observer and the target points are represented by Hobserver and Htarget. Hx defines the height of the place Px. Dox denotes the horizontal distance between the observer Pobserver and Px, and Dxt represents the distance between Px and the target Ptarget. Hx is the highest elevation of the point Px that does not block the sight line between the observer and the target viewpoint.
The following equation is used to compute:
If a target location can be seen from the distant observer point, the following condition must be met:
For the elevation Hx of any location between the two viewpoints Pobserver and Ptarget: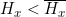 (Equation 2)
(Equation 2)
Considering the size of the grid, the computation of intervisibility using discrete approaches often requires expensive computing resources, which can be accelerated by using parallel algorithms to take advantage of the spatial structure of raster data.
2.2 Continuous Intervisibility Approach
Computational geometry algorithms are employed for calculating the intervisibility of continuous data structures such as TINs where terrains are described as polyhedral surfaces. The strategy used to solve the hidden surface removal (HSR) problem for a 3-dimensional scene is adopted as a continuous intervisibility approach (De Floriani, 1989). Specifically, the visible image of a scene is created by: (1) projecting each face of the terrain surface from the viewpoint, (2) only the visible portions of each face of the scene are maintained using the HSR algorithm.
Figure 3. The visible image of the surfaces. Source: author.
2.3 Intervisibility
Intervisibility analysis determines whether a specific observer point or an object at the observer point can be seen from another viewpoint. For DEM data using the discrete approach, a Boolean value is computed based on whether the line-of-sight is blocked or not. While using the continuous approach for TINs, the visible and invisible areas of the observer point will be partitioned, and where the target viewpoint locate will be examined. An example is illustrated in Figure 4 where a line-of-sight is constructed from the observer point to the target point. The green line indicates the visible part of the line-of-sight, and the red line indicates the invisible part of the line-of-sight. The target point cannot be seen from the observer point as shown in Figure 4 as the line-of-sight is blocked by buildings. It should be noted that intervisibility analysis can be conducted between multiple observer and target viewpoints. However, the computational process is still based on the examination of the visibility relationship between two specified points (i.e., an observer point and a specific target point).
Figure 4. An example of intervisibility between an observer point and a target group. Image source: author, with data from West Virginia View.
2.4 Viewshed Analysis
A viewshed identifies the entire area in the study area that can be observed from one or more viewpoints. To find the viewshed of a specific observation point based on DEM data, the line-of-sights between the observer point and all other cells are computed. The viewshed map is thus represented as an array of Boolean values to indicate whether each grid cell or pixel is visible or invisible. For TINs data, the viewshed can be obtained by overlaying the visibility maps of each terrain face.
Figure 5. An example of a visibility map. Source: author.
Figure 5 shows an example of output for viewshed analysis. The left figure shows the terrain surfaces. One observer point is shown as a gold star, and two target points are shown as gold triangles. In the right figure, the visible area from the observer viewpoint is shown in green, and the invisible area in the output raster is shown in red. Two line-of-sights are constructed between the observer point and target points. Only one target point can be seen from the observer point as indicated by the green line. By assessing the visibility of each location on terrain surfaces from the observer point, the viewshed area can be constructed.
2.5 Reverse Viewshed Analysis
On the other hand, reverse viewshed analysis is utilized to identify the visibility of a given target point from many observer points, i.e., to find the area from which the target viewpoint can be seen (Fisher, 1996). The reverse viewshed analysis, in general, follows the same computing principles as the viewshed analysis to determine whether the line-of-sight between the observer and target points is blocked. However, because the heights of the viewing point and targeting objects may differ from those in the viewshed analysis (even though they may locate at the same position), the results might be different. In addition, it should be acknowledged that the outputs of reverse viewshed analysis are represented as polygons, similar to the viewshed area that contains a set of observer points.
3. Use Cases
In this section, several applications will be illustrated to show how visibility analysis can be used in solving real-world geographical problems. Traditionally, the applications for visibility analysis on terrains can be classified into the following three major categories (De Floriani & Magillo, 1999):
In addition to these three traditional types of applications, several recent use cases such as location accuracy assessment, interactive intervisibility analysis in 3D space, and viewshed analysis on hexagon are introduced in this section.
3.1 Placement of Observation Point Problems
Placement of observation point problems is defined as finding the optimal locations for observation points so that as much of the terrain surface within the study area as possible is visible from at least one viewpoint. The goal of this problem is to either reduce the number of viewpoints to a minimum that covers the target area or to select a fixed number of points and maximize the visible area. For instance, in addition to the existing observer point, adding which candidate observation place would maximize the viewshed area from all viewpoints, as illustrated in Figure 6. Such a problem is relevant to the p-median and p-center problems in spatial optimization. Visibility analysis has been used for locating fire towers, water towers, radar sites, and other applications.
Figure 6. An example of placement of observation point problems. Source: author.
3.2 Line-of-Sight Communication Problems
Finding the minimum number of viewpoints in the construction of a visibility network is referred to as the line-of-sight communication problem (De Floriani et al., 1994). The nodes in this visibility network correspond to observer locations, and the edges indicate the line-of-sights that connect any two consecutive viewpoints. As a result, any two consecutive viewpoints in such a network can be observed from each other. As shown in Figure 7, nearby wireless towers are connected by line-of-sights so that all three wireless towers are linked together. The solution to this problem could be used to build telephone, television, and digital data base stations.
Figure 7. An example of line-of-sight communication problems. Source: author.
3.3 Visible Path Computation Problems
The visible path computation problem refers to route planning considering visibility characteristics in terrains. Given two points (starting and destination point) and one or multiple observation points, the shortest path between the starting point and the destination point is considered a route. In practice, two types of paths are frequently computed when taking visibility qualities into account for route planning: smuggler’s paths and scenic paths. A smuggler’s path refers to a route with no points visible from observation points. On the contrary, a scenic path indicates a path in which all points are visible from the observation points (Lee & Stucky, 1998). The solution of the visible path computation problem has been widely used in several domains such as civil engineering, military activities (e.g., concealed passageways), and tourism route planning.
3.4 Location Accuracy Assessment Problems
In the era of big data, crowdsourcing volunteered geographic information (VGI) has provided a large volume of geospatial data. The quality of VGI data such as location accuracy, data bias, and representativeness, serve as fundamental issues of its usage. Recently, several studies have employed visibility analysis to assess location accuracy. For example, Senaratne et al., (2013) and Kang et al., (2018) used reverse viewshed analysis to examine whether the geotags of photos are correct by investigating if the location of photos falls within the viewshed of the observer viewpoint. Photos taken nearby Eiffel Tower are collected and mapped in Figure 8. According to the reverse viewshed analysis, green dots indicate that people at viewpoints can see the Eiffel Tower, while red dots indicate those photos cannot observe the Eiffel Tower, and their locations may not be trusted.
Figure 8. An example of reverse viewshed analysis result for location correctness checking. Source: author.
3.5 Interactive Intervisibility Analysis in 3D Space
In addition to traditional static intervisibility analysis, researchers can perform dynamic real-time interactive intervisibility analysis in 3D spaces. ArcGIS Pro provides exploratory analysis tools in which users can customize line-of-sights and viewshed by interactively creating them in real-time. As shown in Figure 9, users can create an observer point by clicking on a specific place on terrain (here it refers to buildings). The viewshed along a pre-defined direction will be generated automatically. Users can also customize the parameters of the viewshed analysis such as minimum distance, maximum distance, and direction. Such a tool enables users to have real-time visual feedback in the simulated space.
Figure 9. An example of interactive viewshed analysis in 3d space. Image source: author, with data from West Virginia View.
3.6 Integration with Hexagons, Higher Resolution Imagery, and UAV Imagery
The emergence of several new data sources and models provides new opportunities for intervisibility analysis, and they can be integrated to benefit future applications.
In addition to performing viewshed analysis on raster data based on rectangular or square raster cells, researchers have attempted to calculate viewshed on hexagonal grids (Qiang et al., 2019). To accomplish this, a binary visibility raster map is produced at first, which indicates the visibility of DEMs based on traditional rectangular raster cells. The proportion of a human observer’s viewing angle in a hexagon grid is then computed and multiplied by the viewshed raster map. Finally, the visibility of each hexagon gird is computed by summing up all intersected raster cells. Though traditional grid-based raster data remained important in the analysis, the integration of viewshed analysis with the increasingly popular hexagonal data provides valuable insights for future intervisibility-related studies with more data models.
Also, researchers have utilized higher resolution imagery from remote sensing imagery and unmanned aerial vehicles (UAVs) for modeling terrain surfaces. Such fine-resolution models bring both opportunities and challenges for intervisibility analysis. On the one hand, more fine-grained and precise intervisibility analysis can be performed to provide more accurate assessments and descriptions of viewshed on terrain surfaces. On the other hand, more computational resources are needed for obtaining the results.
4. Visibility Analysis Tools
Visibility analysis is an important component of existing GIS software. GIS software such as ArcGIS, QGIS, GRASS GIS, SAGA GIS, and GDAL, have provided visibility analysis tools for users to complete viewshed-related tasks.
Users can utilize visibility analysis functions based on Spatial Analyst Toolbox and 3D Analyst Toolbox in ArcGIS Pro and ArcMap for viewshed analysis provided by the ArcGIS family of products. TINs and DEM data are supported by these toolboxes. These ArcToolboxes offer a variety of visibility analysis functions including examining intervisibility, generating line of sight and viewsheds. ArcGIS Pro also provides a set of interactive exploratory analysis tools, as mentioned in section 3.5, that allows users to determine the 3D view of the viewshed and light-of-sight from a given observer point, as shown in Figure 4 and Figure 9. The viewshed and light-of-sight can be generated automatically by interactively moving the observer point. In addition, ArcGIS Online offers a “Create Viewshed” feature that allows users to perform viewshed analysis in WebGIS environments.
QGIS provides a Visibility Analysis Plugin that allows users to compute viewshed and examine the visibility of viewpoints (Cuckovic, 2016). More specifically, it provides the following functions including viewshed calculation, intervisibility network calculation, and visibility index. In comparison with ArcGIS, it only supports raster-based elevation data.
In GRASS GIS, the module r.viewshed can be used to determine the viewshed of a point based on a raster DEM. A raster map that indicates the visibility of each cell is produced given an elevation raster and the location of observer points. One unique feature of this algorithm is its optimization of the CPU usage and memory in accelerating the computing process of viewshed analysis. Consequently, r.viewshed is appropriate to compute viewshed even with very large rasters.
SAGA GIS provides the Visibility module for visibility analysis using point vector data and grid data that denotes the elevation of the terrain surface. The output visibility map of this function includes a raster layer that indicates the visibility of each grid cell.
Similarly, GDAL also provides a function gdal_viewshed to calculate the viewshed based on an input raster DEM and a user-defined point. A binary visibility raster will be generated to indicate the visibility of terrains.
In summary, all software and packages abovementioned offer the function to compute viewshed based on observation points and terrain raster layers. More functions are available in the ArcGIS family products and QGIS for more comprehensive visibility analysis.
Cuckovic, Z. (2016). Advanced viewshed analysis: A Quantum GIS plug-in for the analysis of visual landscapes. The Journal of Open Source Software, 1, 32. https://doi.org/10.21105/joss.00032
De Floriani, L. (1989). A pyramidal data structure for triangle-based surface description. IEEE Computer Graphics and Applications, 9(2), 67–78. https://doi.org/10.1109/38.19053
De Floriani, L., & Magillo, P. (1999). Intervisibility on terrains. Geographic Information Systems: Principles, Techniques, Managament and Applications, 543–556.
De Floriani, L., Marzano, P., & Puppo, E. (1994). Line-of-sight communication on terrain models. International Journal of Geographical Information Systems, 8(4), 329–342. https://doi.org/10.1080/02693799408902004
Fisher, P. F. (1996). Extending the applicability of viewsheds in landscape planning. Photogrammetric Engineering and Remote Sensing, 62(11), 1297–1302.
Floriani, L., & Magillo, P. (2003). Algorithms for Visibility Computation on Terrains: A Survey. Environment and Planning B: Planning and Design, 30(5), 709–728. https://doi.org/10.1068/b12979
Inglis, N. C., Vukomanovic, J., Costanza, J., & Singh, K. K. (2022). From viewsheds to viewscapes: Trends in landscape visibility and visual quality research. Landscape and Urban Planning, 224, 104424. https://doi.org/10.1016/j.landurbplan.2022.104424
Kang, Y., Gao, S., & Liang, Y. (2018). Utilizing Reverse Viewshed Analysis in Image Geo-Localization. Proceedings of the 2nd ACM SIGSPATIAL Workshop on Recommendations for Location-Based Services and Social Networks, 1–5. https://doi.org/10.1145/3282825.3282828
Kim, Y.-H., Rana, S., & Wise, S. (2004). Exploring multiple viewshed analysis using terrain features and optimisation techniques. Computers & Geosciences, 30(9–10), 1019–1032. https://doi.org/10.1016/j.cageo.2004.07.008
Lee, J., & Stucky, D. (1998). On applying viewshed analysis for determining least-cost paths on Digital Elevation Models. International Journal of Geographical Information Science, 12(8). https://ezproxy.library.wisc.edu/login?url=https://search.ebscohost.com/...
Llobera, M. (2007). Modeling visibility through vegetation. International Journal of Geographical Information Science, 21(7), 799–810. https://doi.org/10.1080/13658810601169865
Nagy, G. (1994). Terrain visibility. Computers & Graphics, 18(6), 763–773. https://doi.org/10.1016/0097-8493(94)90002-7
Qiang, Y., Shen, S., & Chen, Q. (2019). Visibility analysis of oceanic blue space using digital elevation models. Landscape and Urban Planning, 181, 92–102. https://doi.org/10.1016/j.landurbplan.2018.09.019
Rua, H., Gonçalves, A. B., & Figueiredo, R. (2013). Assessment of the Lines of Torres Vedras defensive system with visibility analysis. Journal of Archaeological Science, 40(4), 2113–2123. https://doi.org/10.1016/j.jas.2012.12.012
Senaratne, H., Bröring, A., & Schreck, T. (2013). Using Reverse Viewshed Analysis to Assess the Location Correctness of Visually Generated VGI: Assessing the Location Correctness of Visually Generated VGI. Transactions in GIS, 17(3), 369–386. https://doi.org/10.1111/tgis.12039
Keywords: