Spatial association broadly describes how the locations and values of samples or observations vary across space. Similarity in both the attribute values and locations of observations can be assessed using measures of spatial association based upon the first law of geography. In this entry, we focus on the measures of spatial autocorrelation that assess the degree of similarity between attribute values of nearby observations across the entire study region. These global measures assess spatial relationships with the combination of spatial proximity as captured in the spatial weights matrix and the attribute similarity as captured by variable covariance (i.e. Moran’s I) or squared difference (i.e. Geary’s C). For categorical data, the join count statistic provides a global measure of spatial association. Two visualization approaches for spatial autocorrelation measures include Moran scatterplots and variograms (also known as semi-variograms).
Author and Citation Info:
Wu, A.-M., and Kemp, K. K. (2019). Global Measures of Spatial Association. The Geographic Information Science & Technology Body of Knowledge (1st Quarter 2019 Edition), John P. Wilson (Ed.). DOI: 10.22224/gistbok/2019.1.12
This entry was published on March 31, 2019.
This Topic is also available in the following editions: DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Global measures of spatial association. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers.(2nd Quarter 2016, first digital)
Spatial association is a general term that encompasses a number of ways in which events, measurements or places are related in space. This relationship may be measured by determining the distance between nearby observations or by assessing whether the value of observations at nearby locations are similar. When similarity in both observations and locations is of interest, we invoke the first law of geography, "Everything is related to everything else, but near things are more related than distant things" (Tobler 1970, 236). Measures of spatial dependence and spatial autocorrelation are based on this fundamental Geographic Information Science principle and these are the concepts most frequently encompassed within the term spatial association. Thus, these are the focus of this entry. Other forms of spatial association, such as spatial interaction and spatial clustering, are covered elsewhere in this collection.
Spatial association can be assessed globally or locally. In global measures, a single statistic is used to provide a general measure of the similarity between neighbors across the entire study region. Local measures call on the principle of spatial heterogeneity, which assumes that the relationships between locations are not constant over the study area; they provide a means of measuring local variation. This entry explores global measures; a companion entry provides details on local measures.
Measures of spatial dependence and spatial autocorrelation generally depend upon the creation of a spatial weights matrix in which the spatial relationships between observations can be recorded. Thus, we begin with a brief introduction to the spatial weights matrix. Then we review a number of methods used to measure spatial association including join count statistics and the most common measures of spatial autocorrelation, Global Moran’s I and Geary’s C. The semivariogram, a method used to depict spatial autocorrelation between samples of continuous fields, is also introduced. Finally, we close the entry with an assessment of limitations, disciplinary applications and software environments of the measures.
Typically denoted as W, a spatial weights matrix records a neighborhood structure for a set of data with n observations as an n x n matrix:
where wijis the weights element that represents the spatial relationship between location i and locationj. The simplest strategy to construct a spatial weights matrix is to define weights as a binary relationship, where wij=1if i and jare "neighbors" and wij=0 if they are not. There are various adjacency rules used to define neighbors. The simplest is adjacency: Rook’s case observationsiand jare neighbors if they share a common edge boundary; Queen’s case neighbors share edges or corner vertices. Figure 1 shows the simple adjacency neighbor structure of counties in Ohio using the county centroids.
Figure 1. Two spatial structures for the counties in the state of Ohio, USA: Rook’s case adjacency (left) and queen’s case adjacency (right). The two neighbor structures are very similar except for the top left corner and the top right corner where the counties share vertices but not edges. Source: authors.
There are a variety of other spatial structure options for assigning neighbors, such as a distance threshold, k nearest neighbors, and Delaunay triangulation. Spatial weights can also be measurements of interaction, such as number of commuters between places, or distance. The choice of a spatial weights matrix is critical for many spatial statistics calculations including spatial autocorrelation measures, and a spatial weights matrix should be carefully selected to reflect the underlying process of the problem being studied.
Spatial autocorrelation refers to the correlation of a variable with itself in a space – therefore it is "autocorrelation." The development of the spatial autocorrelation concept started as early as the late 1940s, but the true breakthrough did not arrive until the 1970s when Cliff and Ord developed the statistical framework to assess regression misspecification by testing spatial randomness of the regression residuals (Moran 1948; Iyer 1949; Geary, 1954; Dacey 1968; Cliff and Ord 1981; Getis et al. 1995; Getis 2007).
Measures of spatial autocorrelation detect the dependence between the values of one attribute due to spatial proximity. In the case of testing for spatial autocorrelation in regression residuals, a statistically significant result implies that the predictor variables do not capture the variances properly. The result is a misspecified regression model. Measures of spatial autocorrelation show spatial patterns in three categories: 1) Positive spatial autocorrelation that indicates similar values are nearby, 2) negative spatial autocorrelation that indicates dissimilar values tend to be together, and 3) zero spatial autocorrelation, or random distribution, meaning no significance in similar or dissimilar values in nearby locations. Figure 2 illustrates the three categories of spatial autocorrelation patterns.
Figure 2. Three categories of spatial autocorrelation patterns: Positive spatial autocorrelation, negative spatial autocorrelation, and no spatial autocorrelation (random). Source: authors.
Conceptually, one can measure spatial autocorrelation within any type of objects (points, lines, polygons), but these measures are usually applied to polygon data (area objects, called lattices in the spatial econometrics literature) with ratio or interval scale data.
A join (or joint) count statistic is a global spatial autocorrelation measure for categorical variables described back in late 1940s but not named until the 1960s by Dacey (Dacey 1968). A join count statistic assumes first-order homogeneity and tests whether the attribute values of a categorical variable at adjacent locations are the same. As its name implies, a join count statistic counts the number of occurrences of each combination of two categories between neighboring pairs of polygons. Since the number of different joins possible between categories grows quickly, the join count statistic is usually only applied when the number of categories is a very small number (e.g. 2-3).
Using a binary category for the county-level poverty in the state of Ohio as an example, a "high-high" join indicates two neighboring counties are both in high poverty rates, a ‘low-low’ join indicates two neighbors are both in low poverty rates, and a "high-low" join indicates one county having a high poverty rate while its neighboring county has a low poverty rate. A positive spatial autocorrelation means the number of "high-high" or "low-low" neighboring join pairs is significantly higher than what we would expect by chance, and a negative spatial autocorrelation means the number of ‘high-low’ neighboring pairs is significantly higher than expected by chance.
The most popular global measure of spatial autocorrelation is Moran’s I Moran 1948). As spatial autocorrelation measures test for the relationship between spatial proximity and the variable similarity, Moran’s I captures these two terms in a spatial weights matrix and the covariance, respectively. Moran’s I can be calculated using the equation below:
The second numerator portion includes a covariance portion -- the product of deviations from the mean of variable x of observations i and j and, its spatial weight element wij indicating how the observations i and j are spatially related. The sum of this product would only equal to the auto-covariance if all elements of the weights matrix are equal to one. The second denominator is the sum of the non-diagonal elements of the weights matrix over the entire study region. A data variance term is used to normalize the value and to ensure that the index (I) is not large simply due to the large values or variability of x.
The spatial weight used in Moran’s Iis often standardized for the rows to sum up to 1. When the weights matrix is row-standardized, , the Moran’s I can be simplified to . Under the row-standardized conditions, a positive Moran’s I depicts a positive spatial autocorrelation and a negative Moran’s I depicts a negative spatial autocorrelation. An example of the 2015 county poverty rate data in the state of Ohio using a spatial weight matrix of Rook’s case adjacency shows some degree of the positive spatial autocorrelation (Moran’s I statistic of 0.344 with a p-value < 0.001). However, Moran’s I is not restricted to [-1, 1] as the actual interval depends on the weights matrix. The midpoint that represents zero spatial autocorrelation is at the expected value of -1 / (1-n). This value would converge on 0 when there are an increasing number of observations that are in a form of a regular-spaced square raster (Chun & Griffith 2013, p11).
When there is a sufficiently large number of observations, we can test the statistical significance of the measure of spatial autocorrelation. The significance test for Moran’s I can be evaluated by a normal test based on the z-score, that tests whether the observed spatial autocorrelation (I) is significantly different from the null hypothesis of spatial randomness. An alternative option in testing for spatial autocorrelation is a random permutation test. This is usually done using the Monte Carlo approach, where the observed attribute values are permuted a large number of times (e.g. 999). For each permutation, they are randomly assigned to the observation locations and the associated Moran’s I is calculated. This allows a reference distribution of results for the given set of observations to be generated so that an inference can be drawn.
While Moran’s I describes spatial association based on covariance (e.g., ), Geary’s C emphasizes on the differences between locations using the squared difference (e.g., (xi - xj)2)). (Geary 1954):
The values of Geary’s C ranges from 0 to a positive number, and can be interpreted as a positive autocorrelation if between 0 to 1 (with stronger positive autocorrelation approaching 0), no spatial autocorrelation if 1, and a negative spatial autocorrelation if above 1 (with stronger negative autocorrelation for a higher value). Geary’s C is more sensitive to the variation of neighborhoods, and therefore Moran’s I is generally the preferred index for measuring global spatial autocorrelation.
There are also graphic approaches to examining spatial autocorrelation. A good way to visualize Moran’s I is to use a Moran scatterplot. Also called the lagged mean plot, a standardized Moran scatterplot displays the deviation of the value of the observation i from the mean against the weighted average of its neighbors’ deviations (the spatially lagged mean deviation ). The slope of a simple linear regression line drawn through the Moran scatterplot is in fact the value of the Moran’s I when it is row-standardized (Anselin 1996). A Moran scatterplot is partitioned into four quadrants:
Quadrant I (Upper-right) as "high-high": Large values surrounded by large values;
Quadrant II (Upper-left) as "low-high": Small values surrounded by large values;
Quadrant III (Lower-left) as "low-low": Small values surrounded by small values;
Quadrant IV (Lower-right) as "high-low": Large values surrounded by small values.
When nearby observations tend to have similar values (i.e. a positive spatial autocorrelation), a linear trend would be seen through the "high-high" and "low-low" quadrants of the Moran scatterplot. On the other hand, if nearby observations tend to have dissimilar values (i.e. a negative spatial autocorrelation), the linear trend would be seen through the "high-low" and "low-high" quadrants of the plot. Using the same county poverty data in Ohio, the Moran scatterplot in Figure 3 clearly shows that some degree of positive spatial autocorrelation exists.
Figure 3. A Moran scatterplot showing some degree of positive spatial autocorrelation exists for the poverty data in the counties in Ohio. The dashed lines show the global mean drawn through each axis. Source: authors.
Another approach to visualize spatial autocorrelation is the variogram. Also confusingly known as a semivariogram, a variogram plots spatial lags (in distance bands) on the x-axis for all pairs of observations against their semivariance (half of the variance for the attribute value for each observation pair) on the y-axis. Semivariance can be estimated using the equation.
where is theempirical semivariance and N is the number of pairs at a given distance of d, and is the sum of the squared difference of the attribute values for all pairs of the observations at that distance band. Notice that both Geary’s C and a variogram calculate the squared differences of the attribute values, but the variogram assesses the values at multiple lags while Geary’s c only provides a single measure. The semivariance reaches a maximum limit at the "sill" at a spatial lag called the "range" as shown in Figure 4. This suggests the furthest distance over which spatial autocorrelation can be observed. When there is a non-zero intercept on the y -axis, this "nugget" suggests that a portion of the semivariance may be autocorrelated at a finer scale than the spatial lag intervals. Several types of models can be used to plot the variogram: Linear, Spherical, Gaussian, Exponential, and Hole Effect etc.
Figure 4. A spherical variogram model showing sill, range and nugget effect. Source: authors.
Global measures of spatial autocorrelation give one single statistic that summarizes whether the values (of the single variable) are similar to their neighbors across the entire study region. It, however, does not tell us where the similarity (or dissimilarity) occurs. As such, one cannot identify where the similar values (i.e. positive spatial autocorrelation) are located using global measures of spatial association. Local measures of spatial association and other clustering techniques (e.g. scan statistics) are required in order to answer that question of "where." Global measures of spatial association have been widely used to understand spatial patterns indicative of underlying processes in various disciplines, including ecology, econometrics, epidemiology, criminology, and geosciences, to name a few. Example studies include spatial distribution patterns for disease incidences (Martins-Melo et al. 2012, Wu et al. 2011), exploring species abundance and species distributions (Dormann et al. 2007), and identifying spatial patterns for understanding land use change effect and geomorphic development (Pérez-Peña et al. 2009, Guo et al. 2013).
Today, measuring global spatial association can be done in various computing environments including proprietary software, such as ArcGIS, SAS, and MatLab, as well as open-source software or freeware, including GeoDa, FRAGSTATS and R (e.g. sp, spdep, ads, lctools, DCluster and spatstat packages).
References:
Anselin, L. (1996). The Moran scatterplot as an ESDA tool to assess local instability in spatial association. In Spatial Analytical Perspectives on GIS, eds. M. Fischer, H. Scholten & D. Unwin, 111-125. London: Taylor and Francis.
Chun, Y., & Griffith, D. A. (2013). Spatial statistics and geostatistics: theory and applications for geographic information science and technology. (pp. 8-22). London, UK: Sage.
Dormann, C.F., McPherson, J.M., Araújo, M.B., Bivand, R., Bolliger, J., Carl, G, Davies, R.G., Hirzel, A., Jets, W., Kissling, W.D., Kühn, I, Ohlemüller, R., Peres-Neto, P.R., Reineking, B., Schröder, B., Schurr, F.M. & Wilson, R. (2007). Methods to account for spatial autocorrelation in the analysis of species distributional data: a review. Ecography, 30(5), 609-628.
Dacey, M. F. (1968). A review on measures of contiguity for two and k-color maps.In: B. J. L.Berry & D. F Marble (Eds.). Spatial analysis: a reader in statistical geography. Englewood Cliffs, NJ: Prentice-Hall.
Geary, R. C. (1954). The contiguity ratio and statistical mapping. The incorporated statistician, 5(3), 115-146.
Getis, A. (2007). Reflections on spatial autocorrelation. Regional Science and Urban Economics 37(4): 491-496.
Guo, L., Du, S., Haining, R., & Zhang, L. (2013). Global and local indicators of spatial association between points and polygons: a study of land use change. International Journal of Applied Earth Observation and Geoinformation, 21, 384-396.
Iyer, P. K. (1949). The first and second moments of some probability distributions arising from points on a lattice and their application. Biometrika, 135-141.
Martins‐Melo, F. R., Ramos, A. N., Alencar, C. H., Lange, W., & Heukelbach, J. (2012). Mortality of Chagas’ disease in Brazil: spatial patterns and definition of high‐risk areas. Tropical Medicine & International Health, 17(9), 1066-1075.
Moran, P. A. (1948). The interpretation of statistical maps. Journal of the Royal Statistical Society. Series B (Methodological), 10(2), 243-251.
Pérez‐Peña, J. V., Azañón, J. M., Booth‐Rea, G., Azor, A., & Delgado, J. (2009). Differentiating geology and tectonics using a spatial autocorrelation technique for the hypsometric integral. Journal of Geophysical Research: Earth Surface, 114(F2).
Tobler, W.R. (1970) A computer movie simulating urban growth in the Detroit region. Economic Geography, 46: 234-240.
Wu, W., Junqiao, G. Guan, P., Sun, Y., Zhou, B. (2011). Clusters of spatial, temporal, and space-time distribution of hemorrhagic fever with renal syndrome in Liaoning Province, Northeastern China. BMC Infectious Diseases 11(1):229.
Learning Objectives:
Define spatial autocorrelation.
Describe how spatial weights are used to calculate measures of spatial autocorrelation.
Discuss how Moran’s I and Geary’s C are used to measure spatial patterns.
Identify the proper data type for join count statistics and compute the statistic.
Compute and interpret a Moran scatterplot.
Explain how a variogram depicts a global assessment of spatial association.
Instructional Assessment Questions:
What is the spatial weights matrix? How is it used in assessing spatial autocorrelation?
Name a measure appropriate for assessing spatial dependency of polygon data measured in interval or ratio scales. What measure might be appropriate for categorical attribute data?
What are the similarities and differences between Moran’s I and Geary’s C?
Explain how the random permutation test can be used to support inference in assessing spatial autocorrelation.
Spatial association broadly describes how the locations and values of samples or observations vary across space. Similarity in both the attribute values and locations of observations can be assessed using measures of spatial association based upon the first law of geography. In this entry, we focus on the measures of spatial autocorrelation that assess the degree of similarity between attribute values of nearby observations across the entire study region. These global measures assess spatial relationships with the combination of spatial proximity as captured in the spatial weights matrix and the attribute similarity as captured by variable covariance (i.e. Moran’s I) or squared difference (i.e. Geary’s C). For categorical data, the join count statistic provides a global measure of spatial association. Two visualization approaches for spatial autocorrelation measures include Moran scatterplots and variograms (also known as semi-variograms).
Wu, A.-M., and Kemp, K. K. (2019). Global Measures of Spatial Association. The Geographic Information Science & Technology Body of Knowledge (1st Quarter 2019 Edition), John P. Wilson (Ed.). DOI: 10.22224/gistbok/2019.1.12
This entry was published on March 31, 2019.
This Topic is also available in the following editions: DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Global measures of spatial association. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital)
1. Introduction
Spatial association is a general term that encompasses a number of ways in which events, measurements or places are related in space. This relationship may be measured by determining the distance between nearby observations or by assessing whether the value of observations at nearby locations are similar. When similarity in both observations and locations is of interest, we invoke the first law of geography, "Everything is related to everything else, but near things are more related than distant things" (Tobler 1970, 236). Measures of spatial dependence and spatial autocorrelation are based on this fundamental Geographic Information Science principle and these are the concepts most frequently encompassed within the term spatial association. Thus, these are the focus of this entry. Other forms of spatial association, such as spatial interaction and spatial clustering, are covered elsewhere in this collection.
Spatial association can be assessed globally or locally. In global measures, a single statistic is used to provide a general measure of the similarity between neighbors across the entire study region. Local measures call on the principle of spatial heterogeneity, which assumes that the relationships between locations are not constant over the study area; they provide a means of measuring local variation. This entry explores global measures; a companion entry provides details on local measures.
Measures of spatial dependence and spatial autocorrelation generally depend upon the creation of a spatial weights matrix in which the spatial relationships between observations can be recorded. Thus, we begin with a brief introduction to the spatial weights matrix. Then we review a number of methods used to measure spatial association including join count statistics and the most common measures of spatial autocorrelation, Global Moran’s I and Geary’s C. The semivariogram, a method used to depict spatial autocorrelation between samples of continuous fields, is also introduced. Finally, we close the entry with an assessment of limitations, disciplinary applications and software environments of the measures.
2. Spatial Weights Matrix
Typically denoted as W, a spatial weights matrix records a neighborhood structure for a set of data with n observations as an n x n matrix:
where wij is the weights element that represents the spatial relationship between location i and location j. The simplest strategy to construct a spatial weights matrix is to define weights as a binary relationship, where wij=1 if i and j are "neighbors" and wij=0 if they are not. There are various adjacency rules used to define neighbors. The simplest is adjacency: Rook’s case observations i and j are neighbors if they share a common edge boundary; Queen’s case neighbors share edges or corner vertices. Figure 1 shows the simple adjacency neighbor structure of counties in Ohio using the county centroids.
Figure 1. Two spatial structures for the counties in the state of Ohio, USA: Rook’s case adjacency (left) and queen’s case adjacency (right). The two neighbor structures are very similar except for the top left corner and the top right corner where the counties share vertices but not edges. Source: authors.
There are a variety of other spatial structure options for assigning neighbors, such as a distance threshold, k nearest neighbors, and Delaunay triangulation. Spatial weights can also be measurements of interaction, such as number of commuters between places, or distance. The choice of a spatial weights matrix is critical for many spatial statistics calculations including spatial autocorrelation measures, and a spatial weights matrix should be carefully selected to reflect the underlying process of the problem being studied.
3. Spatial Autocorrelation
Spatial autocorrelation refers to the correlation of a variable with itself in a space – therefore it is "autocorrelation." The development of the spatial autocorrelation concept started as early as the late 1940s, but the true breakthrough did not arrive until the 1970s when Cliff and Ord developed the statistical framework to assess regression misspecification by testing spatial randomness of the regression residuals (Moran 1948; Iyer 1949; Geary, 1954; Dacey 1968; Cliff and Ord 1981; Getis et al. 1995; Getis 2007).
Measures of spatial autocorrelation detect the dependence between the values of one attribute due to spatial proximity. In the case of testing for spatial autocorrelation in regression residuals, a statistically significant result implies that the predictor variables do not capture the variances properly. The result is a misspecified regression model. Measures of spatial autocorrelation show spatial patterns in three categories: 1) Positive spatial autocorrelation that indicates similar values are nearby, 2) negative spatial autocorrelation that indicates dissimilar values tend to be together, and 3) zero spatial autocorrelation, or random distribution, meaning no significance in similar or dissimilar values in nearby locations. Figure 2 illustrates the three categories of spatial autocorrelation patterns.
Figure 2. Three categories of spatial autocorrelation patterns: Positive spatial autocorrelation, negative spatial autocorrelation, and no spatial autocorrelation (random). Source: authors.
Conceptually, one can measure spatial autocorrelation within any type of objects (points, lines, polygons), but these measures are usually applied to polygon data (area objects, called lattices in the spatial econometrics literature) with ratio or interval scale data.
4. Join Count Statistics
A join (or joint) count statistic is a global spatial autocorrelation measure for categorical variables described back in late 1940s but not named until the 1960s by Dacey (Dacey 1968). A join count statistic assumes first-order homogeneity and tests whether the attribute values of a categorical variable at adjacent locations are the same. As its name implies, a join count statistic counts the number of occurrences of each combination of two categories between neighboring pairs of polygons. Since the number of different joins possible between categories grows quickly, the join count statistic is usually only applied when the number of categories is a very small number (e.g. 2-3).
Using a binary category for the county-level poverty in the state of Ohio as an example, a "high-high" join indicates two neighboring counties are both in high poverty rates, a ‘low-low’ join indicates two neighbors are both in low poverty rates, and a "high-low" join indicates one county having a high poverty rate while its neighboring county has a low poverty rate. A positive spatial autocorrelation means the number of "high-high" or "low-low" neighboring join pairs is significantly higher than what we would expect by chance, and a negative spatial autocorrelation means the number of ‘high-low’ neighboring pairs is significantly higher than expected by chance.
5. Global Moran's I and Geary's C
The most popular global measure of spatial autocorrelation is Moran’s I Moran 1948). As spatial autocorrelation measures test for the relationship between spatial proximity and the variable similarity, Moran’s I captures these two terms in a spatial weights matrix and the covariance, respectively. Moran’s I can be calculated using the equation below:
The second numerator portion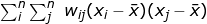 includes a covariance portion -- the product of deviations from the mean of variable x of observations i and j and, its spatial weight element wij indicating how the observations i and j are spatially related. The sum of this product would only equal to the auto-covariance if all elements of the weights matrix are equal to one. The second denominator is the sum of the non-diagonal elements of the weights matrix
includes a covariance portion -- the product of deviations from the mean of variable x of observations i and j and, its spatial weight element wij indicating how the observations i and j are spatially related. The sum of this product would only equal to the auto-covariance if all elements of the weights matrix are equal to one. The second denominator is the sum of the non-diagonal elements of the weights matrix 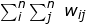 over the entire study region. A data variance term is used to normalize the value and to ensure that the index (I) is not large simply due to the large values or variability of x.
over the entire study region. A data variance term is used to normalize the value and to ensure that the index (I) is not large simply due to the large values or variability of x.
The spatial weight used in Moran’s I is often standardized for the rows to sum up to 1. When the weights matrix is row-standardized,
is often standardized for the rows to sum up to 1. When the weights matrix is row-standardized, 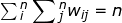 , the Moran’s I can be simplified to . Under the row-standardized conditions, a positive Moran’s I depicts a positive spatial autocorrelation and a negative Moran’s I depicts a negative spatial autocorrelation. An example of the 2015 county poverty rate data in the state of Ohio using a spatial weight matrix of Rook’s case adjacency shows some degree of the positive spatial autocorrelation (Moran’s I statistic of 0.344 with a p-value < 0.001). However, Moran’s I is not restricted to [-1, 1] as the actual interval depends on the weights matrix. The midpoint that represents zero spatial autocorrelation is at the expected value of -1 / (1-n). This value would converge on 0 when there are an increasing number of observations that are in a form of a regular-spaced square raster (Chun & Griffith 2013, p11).
, the Moran’s I can be simplified to . Under the row-standardized conditions, a positive Moran’s I depicts a positive spatial autocorrelation and a negative Moran’s I depicts a negative spatial autocorrelation. An example of the 2015 county poverty rate data in the state of Ohio using a spatial weight matrix of Rook’s case adjacency shows some degree of the positive spatial autocorrelation (Moran’s I statistic of 0.344 with a p-value < 0.001). However, Moran’s I is not restricted to [-1, 1] as the actual interval depends on the weights matrix. The midpoint that represents zero spatial autocorrelation is at the expected value of -1 / (1-n). This value would converge on 0 when there are an increasing number of observations that are in a form of a regular-spaced square raster (Chun & Griffith 2013, p11).
When there is a sufficiently large number of observations, we can test the statistical significance of the measure of spatial autocorrelation. The significance test for Moran’s I can be evaluated by a normal test based on the z-score, that tests whether the observed spatial autocorrelation (I) is significantly different from the null hypothesis of spatial randomness. An alternative option in testing for spatial autocorrelation is a random permutation test. This is usually done using the Monte Carlo approach, where the observed attribute values are permuted a large number of times (e.g. 999). For each permutation, they are randomly assigned to the observation locations and the associated Moran’s I is calculated. This allows a reference distribution of results for the given set of observations to be generated so that an inference can be drawn.
While Moran’s I describes spatial association based on covariance (e.g.,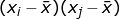 ), Geary’s C emphasizes on the differences between locations using the squared difference (e.g., (xi - xj)2)). (Geary 1954):
), Geary’s C emphasizes on the differences between locations using the squared difference (e.g., (xi - xj)2)). (Geary 1954):
The values of Geary’s C ranges from 0 to a positive number, and can be interpreted as a positive autocorrelation if between 0 to 1 (with stronger positive autocorrelation approaching 0), no spatial autocorrelation if 1, and a negative spatial autocorrelation if above 1 (with stronger negative autocorrelation for a higher value). Geary’s C is more sensitive to the variation of neighborhoods, and therefore Moran’s I is generally the preferred index for measuring global spatial autocorrelation.
6. Moran Scatterplot and Variogram
There are also graphic approaches to examining spatial autocorrelation. A good way to visualize Moran’s I is to use a Moran scatterplot. Also called the lagged mean plot, a standardized Moran scatterplot displays the deviation of the value of the observation i from the mean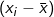 against the weighted average of its neighbors’ deviations (the spatially lagged mean deviation
against the weighted average of its neighbors’ deviations (the spatially lagged mean deviation 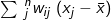 ). The slope of a simple linear regression line drawn through the Moran scatterplot is in fact the value of the Moran’s I when it is row-standardized (Anselin 1996). A Moran scatterplot is partitioned into four quadrants:
). The slope of a simple linear regression line drawn through the Moran scatterplot is in fact the value of the Moran’s I when it is row-standardized (Anselin 1996). A Moran scatterplot is partitioned into four quadrants:
When nearby observations tend to have similar values (i.e. a positive spatial autocorrelation), a linear trend would be seen through the "high-high" and "low-low" quadrants of the Moran scatterplot. On the other hand, if nearby observations tend to have dissimilar values (i.e. a negative spatial autocorrelation), the linear trend would be seen through the "high-low" and "low-high" quadrants of the plot. Using the same county poverty data in Ohio, the Moran scatterplot in Figure 3 clearly shows that some degree of positive spatial autocorrelation exists.
Figure 3. A Moran scatterplot showing some degree of positive spatial autocorrelation exists for the poverty data in the counties in Ohio. The dashed lines show the global mean drawn through each axis. Source: authors.
Another approach to visualize spatial autocorrelation is the variogram. Also confusingly known as a semivariogram, a variogram plots spatial lags (in distance bands) on the x-axis for all pairs of observations against their semivariance (half of the variance for the attribute value for each observation pair) on the y-axis. Semivariance can be estimated using the equation.
where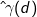 is the empirical semivariance and N is the number of pairs at a given distance of d, and
is the empirical semivariance and N is the number of pairs at a given distance of d, and 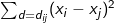 is the sum of the squared difference of the attribute values for all pairs of the observations at that distance band. Notice that both Geary’s C and a variogram calculate the squared differences of the attribute values, but the variogram assesses the values at multiple lags while Geary’s c only provides a single measure. The semivariance reaches a maximum limit at the "sill" at a spatial lag called the "range" as shown in Figure 4. This suggests the furthest distance over which spatial autocorrelation can be observed. When there is a non-zero intercept on the y -axis, this "nugget" suggests that a portion of the semivariance may be autocorrelated at a finer scale than the spatial lag intervals. Several types of models can be used to plot the variogram: Linear, Spherical, Gaussian, Exponential, and Hole Effect etc.
is the sum of the squared difference of the attribute values for all pairs of the observations at that distance band. Notice that both Geary’s C and a variogram calculate the squared differences of the attribute values, but the variogram assesses the values at multiple lags while Geary’s c only provides a single measure. The semivariance reaches a maximum limit at the "sill" at a spatial lag called the "range" as shown in Figure 4. This suggests the furthest distance over which spatial autocorrelation can be observed. When there is a non-zero intercept on the y -axis, this "nugget" suggests that a portion of the semivariance may be autocorrelated at a finer scale than the spatial lag intervals. Several types of models can be used to plot the variogram: Linear, Spherical, Gaussian, Exponential, and Hole Effect etc.
Figure 4. A spherical variogram model showing sill, range and nugget effect. Source: authors.
7. Limitations and Applications of Global Spatial Association
Global measures of spatial autocorrelation give one single statistic that summarizes whether the values (of the single variable) are similar to their neighbors across the entire study region. It, however, does not tell us where the similarity (or dissimilarity) occurs. As such, one cannot identify where the similar values (i.e. positive spatial autocorrelation) are located using global measures of spatial association. Local measures of spatial association and other clustering techniques (e.g. scan statistics) are required in order to answer that question of "where." Global measures of spatial association have been widely used to understand spatial patterns indicative of underlying processes in various disciplines, including ecology, econometrics, epidemiology, criminology, and geosciences, to name a few. Example studies include spatial distribution patterns for disease incidences (Martins-Melo et al. 2012, Wu et al. 2011), exploring species abundance and species distributions (Dormann et al. 2007), and identifying spatial patterns for understanding land use change effect and geomorphic development (Pérez-Peña et al. 2009, Guo et al. 2013).
Today, measuring global spatial association can be done in various computing environments including proprietary software, such as ArcGIS, SAS, and MatLab, as well as open-source software or freeware, including GeoDa, FRAGSTATS and R (e.g. sp, spdep, ads, lctools, DCluster and spatstat packages).
Anselin, L. (1996). The Moran scatterplot as an ESDA tool to assess local instability in spatial association. In Spatial Analytical Perspectives on GIS, eds. M. Fischer, H. Scholten & D. Unwin, 111-125. London: Taylor and Francis.
Chun, Y., & Griffith, D. A. (2013). Spatial statistics and geostatistics: theory and applications for geographic information science and technology. (pp. 8-22). London, UK: Sage.
Dormann, C.F., McPherson, J.M., Araújo, M.B., Bivand, R., Bolliger, J., Carl, G, Davies, R.G., Hirzel, A., Jets, W., Kissling, W.D., Kühn, I, Ohlemüller, R., Peres-Neto, P.R., Reineking, B., Schröder, B., Schurr, F.M. & Wilson, R. (2007). Methods to account for spatial autocorrelation in the analysis of species distributional data: a review. Ecography, 30(5), 609-628.
Dacey, M. F. (1968). A review on measures of contiguity for two and k-color maps.In: B. J. L.Berry & D. F Marble (Eds.). Spatial analysis: a reader in statistical geography. Englewood Cliffs, NJ: Prentice-Hall.
Geary, R. C. (1954). The contiguity ratio and statistical mapping. The incorporated statistician, 5(3), 115-146.
Getis, A. (2007). Reflections on spatial autocorrelation. Regional Science and Urban Economics 37(4): 491-496.
Guo, L., Du, S., Haining, R., & Zhang, L. (2013). Global and local indicators of spatial association between points and polygons: a study of land use change. International Journal of Applied Earth Observation and Geoinformation, 21, 384-396.
Iyer, P. K. (1949). The first and second moments of some probability distributions arising from points on a lattice and their application. Biometrika, 135-141.
Martins‐Melo, F. R., Ramos, A. N., Alencar, C. H., Lange, W., & Heukelbach, J. (2012). Mortality of Chagas’ disease in Brazil: spatial patterns and definition of high‐risk areas. Tropical Medicine & International Health, 17(9), 1066-1075.
Moran, P. A. (1948). The interpretation of statistical maps. Journal of the Royal Statistical Society. Series B (Methodological), 10(2), 243-251.
Pérez‐Peña, J. V., Azañón, J. M., Booth‐Rea, G., Azor, A., & Delgado, J. (2009). Differentiating geology and tectonics using a spatial autocorrelation technique for the hypsometric integral. Journal of Geophysical Research: Earth Surface, 114(F2).
Tobler, W.R. (1970) A computer movie simulating urban growth in the Detroit region. Economic Geography, 46: 234-240.
Wu, W., Junqiao, G. Guan, P., Sun, Y., Zhou, B. (2011). Clusters of spatial, temporal, and space-time distribution of hemorrhagic fever with renal syndrome in Liaoning Province, Northeastern China. BMC Infectious Diseases 11(1):229.
Keywords: