AM-57 - Data conversion

- Identify the conceptual and practical difficulties associated with data model and format conversion
- Convert a data set from the native format of one GIS product to another
- Discuss the role of metadata in facilitating conversation of data models and data structures between systems
- Describe a workflow for converting and implementing a data model in a GIS involving an Entity-Relationship (E-R) diagram and the Universal Modeling Language (UML)

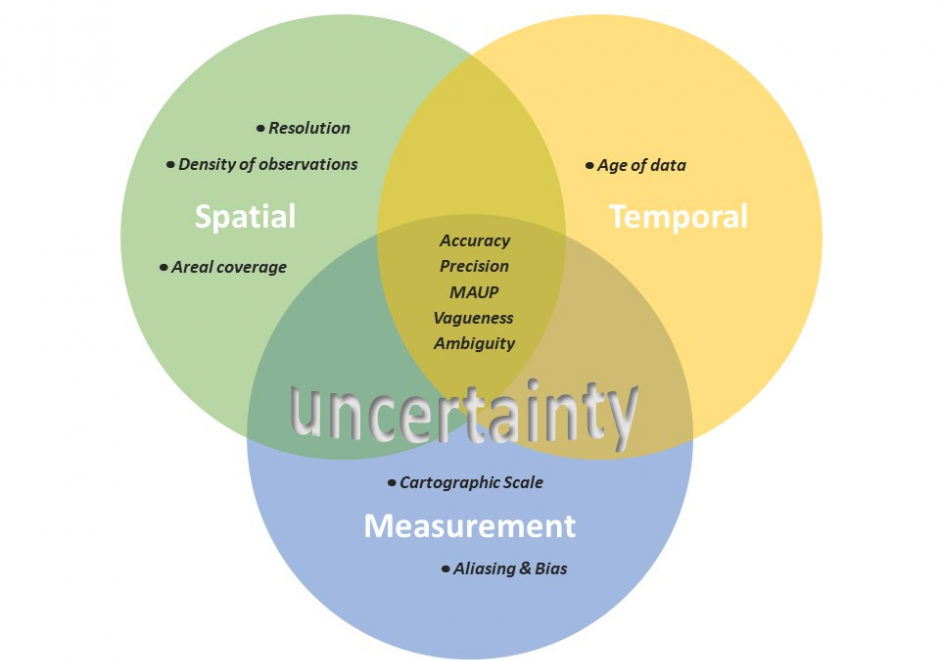


AM-90 - Computational Movement Analysis
Figure 1. Group movement patterns as illustrated in this coordinated escape behavior of a group of mountain goat (Rubicapra rubicapra) evading approaching hikers on the Fuorcla Trupchun near the Italian/Swiss border are at the core of computational movement analysis. Once the trajectories of moving objects are collected and made accessible for computational processing, CMA aims at a better understanding of the characteristics of movement processes of animals, people or things in geographic space.
Computational Movement Analysis (CMA) develops and applies analytical computational tools aiming at a better understanding of movement data. CMA copes with the rapidly growing data streams capturing the mobility of people, animals, and things roaming geographic spaces. CMA studies how movement can be represented, modeled, and analyzed in GIS&T. The CMA toolbox includes a wide variety of approaches, ranging from database research, over computational geometry to data mining and visual analytics.