CV-32 - Cartograms
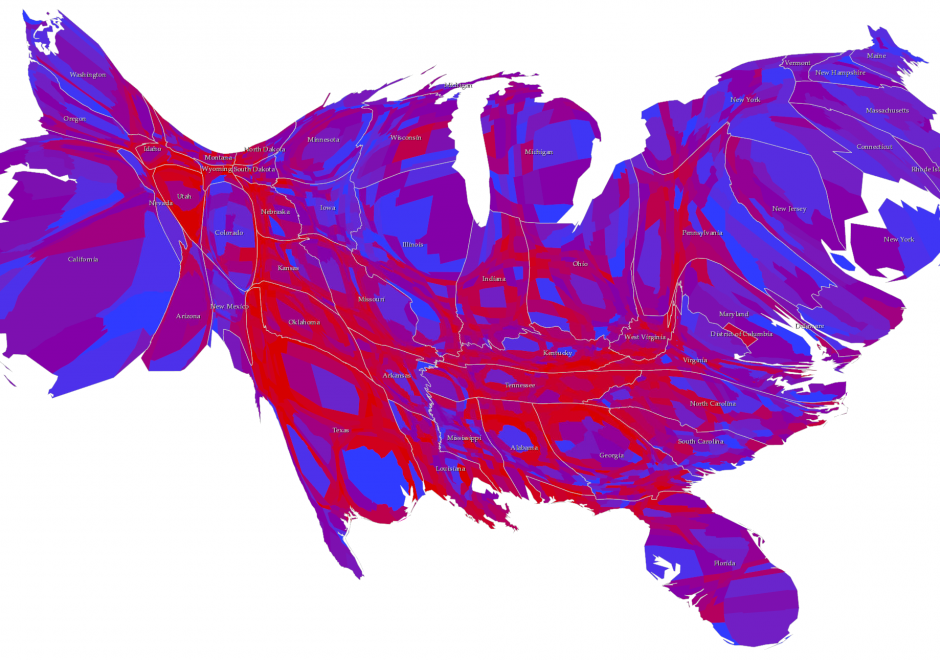
Cartograms are used for thematic mapping. They are a particular class of map type where some aspect of the geometry of the map is modified to accommodate the problem caused by perceptually different geographies. Standard thematic maps, such as the choropleth, have inherent biases simply due to the fact that areas will likely be very different in size from one another. The tendency to see larger areas as more important, regardless of the variable being mapped, can cause confusion. Cartograms tackle this by modifying the geography, effectively normalizing it to create a map where each area takes on a new shape and/or size based on the variable being mapped. Cartograms therefore depict geographical space diagrammatically as they lose their relationship with true coordinate system geometry. There are four main types of cartogram which each represent the mapped variable differently – non-contiguous, contiguous, graphical and gridded.



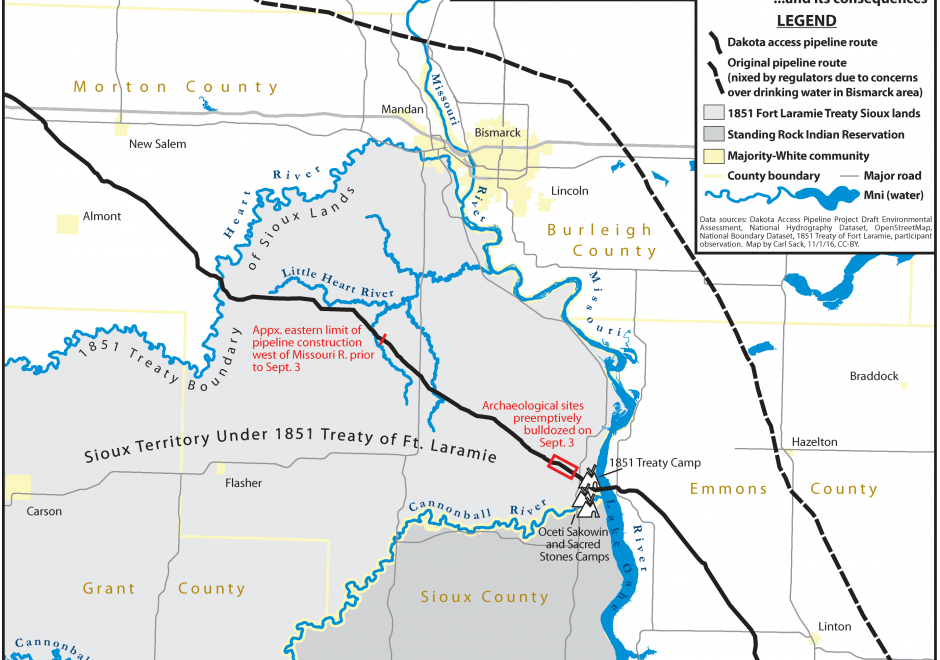


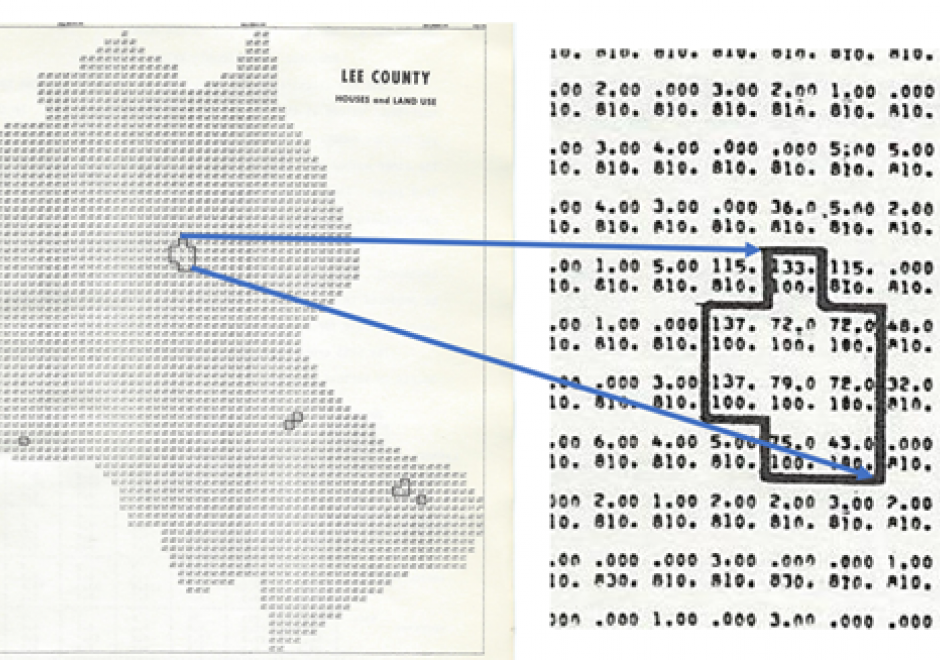

AM-80 - Capturing Spatiotemporal Dynamics in Computational Modeling
We live in a dynamic world that includes various types of changes at different locations over time in natural environments as well as in human societies. Modern sensing technology, location-aware technology and mobile technology have made it feasible to collect spatiotemporal tracking data at a high spatial and temporal granularity and at affordable costs. Coupled with powerful information and communication technologies, we now have much better data and computing platforms to pursue computational modeling of spatiotemporal dynamics. Researchers have attempted to better understand various kinds of spatiotemporal dynamics in order to predict, or even control, future changes of certain phenomena. A simple approach to representing spatiotemporal dynamics is by adding time (t) to the spatial dimensions (x,y,z) of each feature. However, spatiotemporal dynamics in the real world are more complex than a simple representation of (x,y,z,t) that describes the location of a feature at a given time. This article presents selected concepts, computational modeling approaches, and sample applications that provide a foundation to computational modeling of spatiotemporal dynamics. We also indicate why the research of spatiotemporal dynamics is important to geographic information systems (GIS) and geographic information science (GIScience), especially from a temporal GIS perspective.