DM-60 - Spatial Data Infrastructures
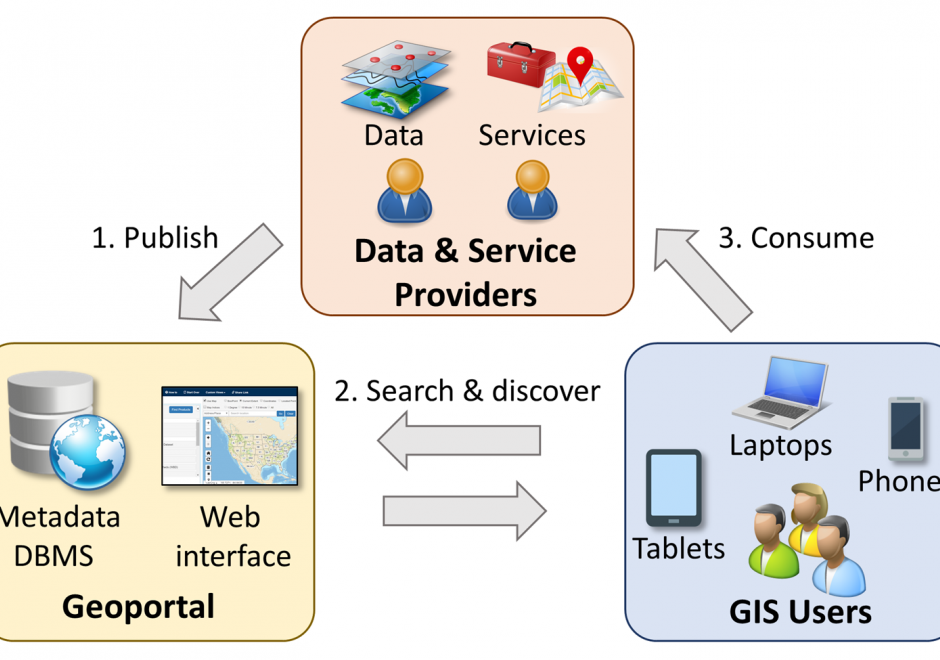
Spatial data infrastructure (SDI) is the infrastructure that facilitates the discovery, access, management, distribution, reuse, and preservation of digital geospatial resources. These resources may include maps, data, geospatial services, and tools. As cyberinfrastructures, SDIs are similar to other infrastructures, such as water supplies and transportation networks, since they play fundamental roles in many aspects of the society. These roles have become even more significant in today’s big data age, when a large volume of geospatial data and Web services are available. From a technological perspective, SDIs mainly consist of data, hardware, and software. However, a truly functional SDI also needs the efforts of people, supports from organizations, government policies, data and software standards, and many others. In this chapter, we will present the concepts and values of SDIs, as well as a brief history of SDI development in the U.S. We will also discuss the components of a typical SDI, and will specifically focus on three key components: geoportals, metadata, and search functions. Examples of the existing SDI implementations will also be discussed.



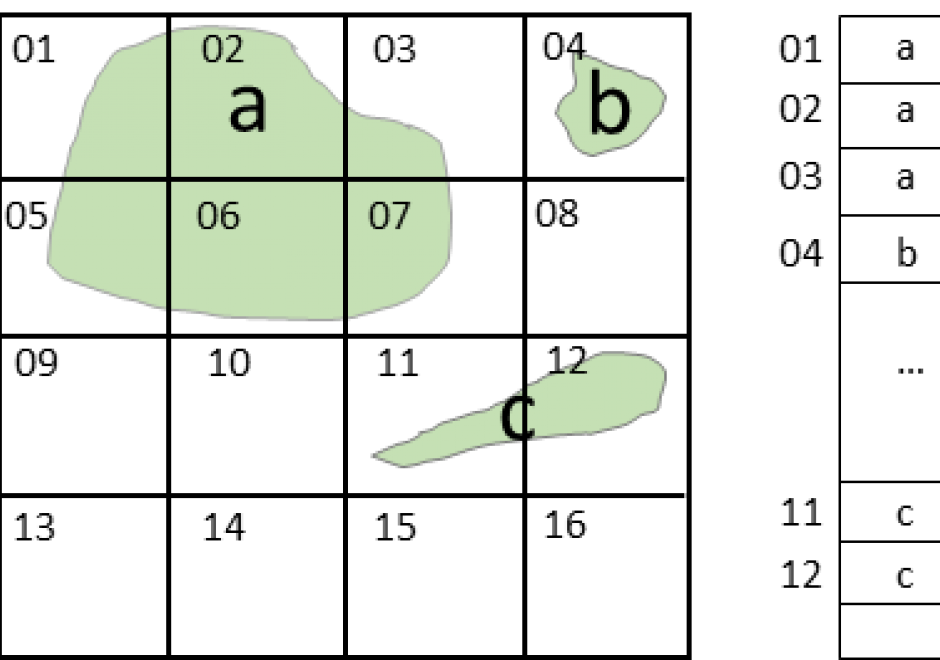
FC-37 - Spatial Autocorrelation
The scientific term spatial autocorrelation describes Tobler’s first law of geography: everything is related to everything else, but nearby things are more related than distant things. Spatial autocorrelation has a:
Positive spatial autocorrelation constitutes the focal point of its past and present; one expectation is that negative spatial autocorrelation will become a focal point of its future.