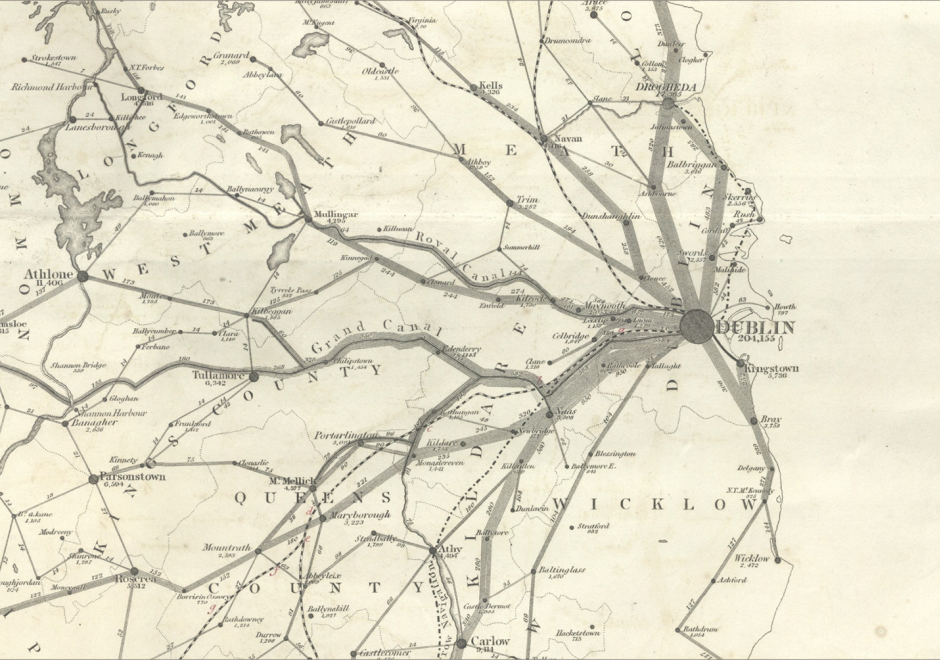
FC-14 - Directional Operations

In the same manner as distance, direction plays an equally important role in GIS. This article first summarizes different ways of measuring direction, either quantitatively or qualitatively. Formulas and examples are provided. In the following discussion, fundamental differences between distance and direction in describing spatial relations is examined; properties of angles are emphasized in the context of GIS; and the classification of both cardinal and projective direction is illustrated. With a focus on quantitative operations, various directional operations are categorized and elaborated based on factors such as the underlying data model (vector or raster) and whether direction effect is explicitly or implicitly embedded in the data.

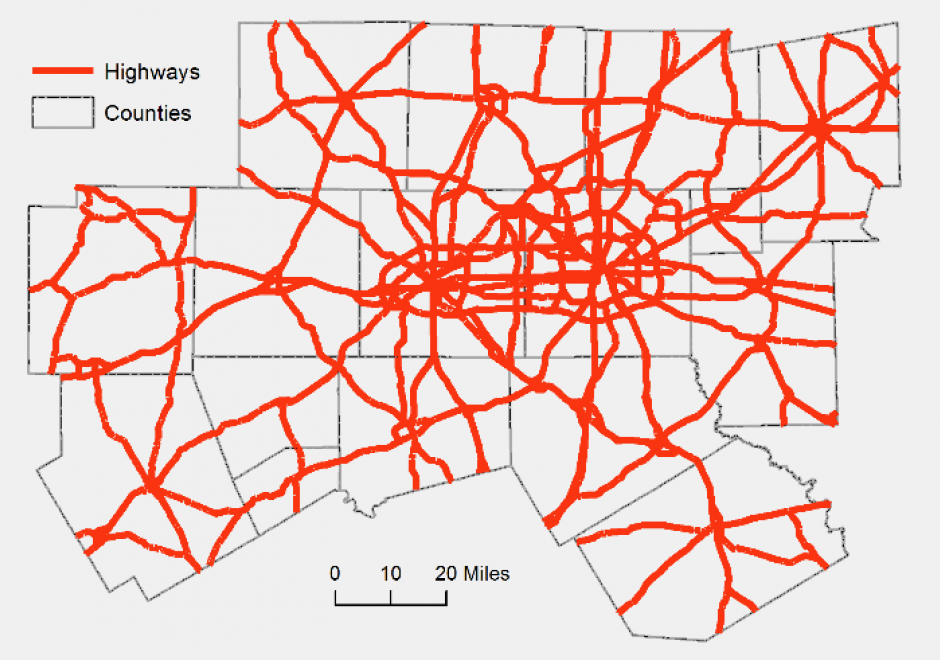
FC-19 - Networks
A network is a widely used term with different definitions and methodologies depending on the applications. In GIS, a network refers to an arrangement of elements (i.e., nodes, links) and information on their connections and interactions. There are two types of networks: physical and logical. While a physical network has tangible objects (e.g., road segments), a logical network represents logical connections among nodes and links. A network can be represented with a mathematical notion called graph theory. Different network components are utilized to describe characteristics of a network including loops, walks, paths, circuits, and parallel edges. Network data are commonly organized in a vector format with network topology, specifically connectivity among nodes and links, whereas raster data can be also utilized for a least-cost problem over continuous space. Network data is utilized in a wide range of network analyses, including the classic shortest path problem.