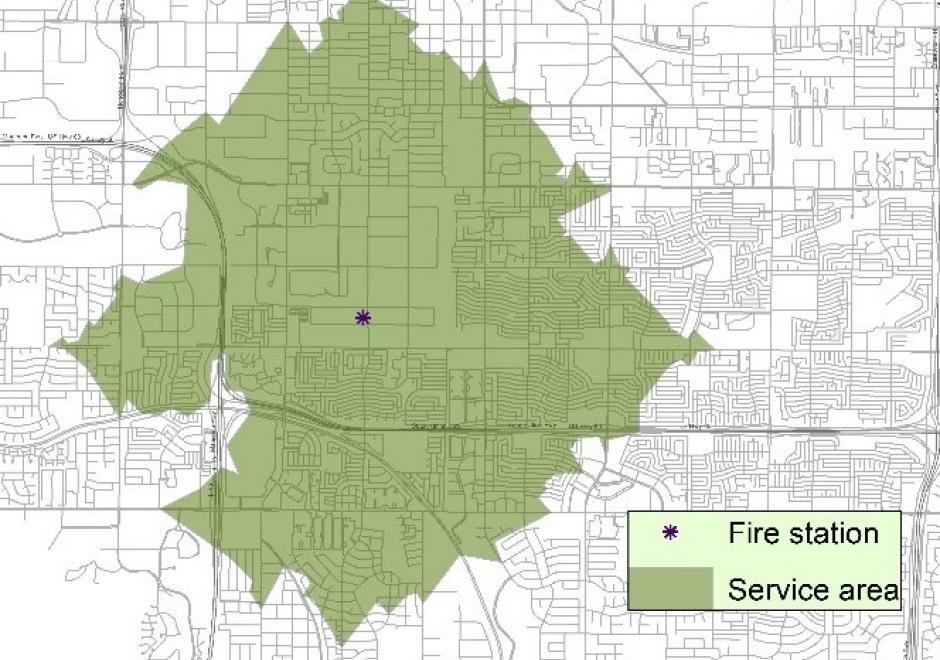
AM-17 - Intervisibility, Line-of-Sight, and Viewsheds
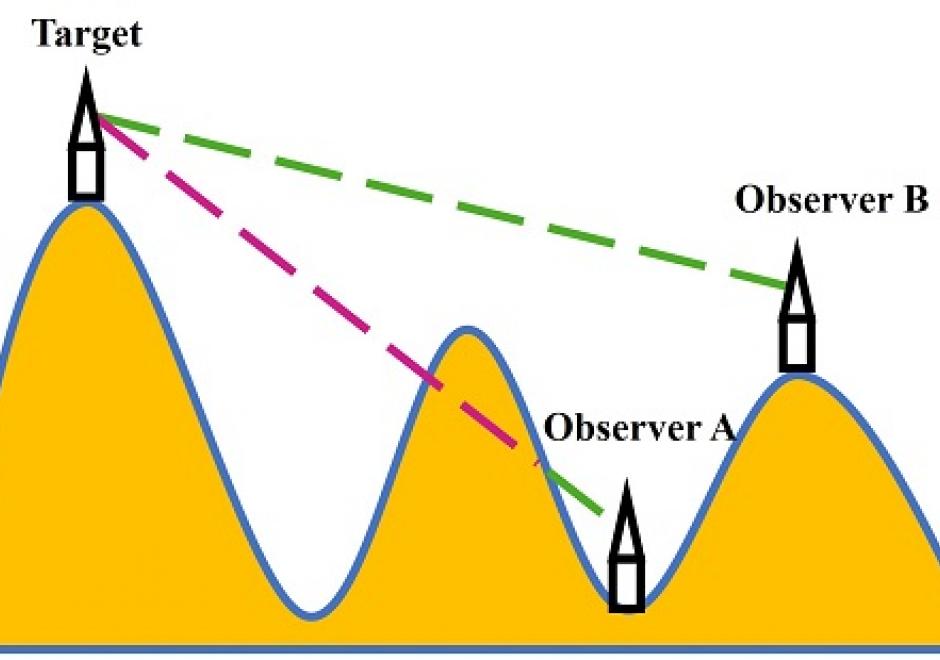
The visibility of a place refers to whether it can be seen by observers from one or multiple other locations. Modeling the visibility of points has various applications in GIS, such as placement of observation points, military observation, line-of-sight communication, optimal path route planning, and urban design. This chapter provides a brief introduction to visibility analysis, including an overview of basic conceptions in visibility analysis, the methods for computing intervisibility using discrete and continuous approaches based on DEM and TINs, the process of intervisibility analysis, viewshed and reverse viewshed analysis. Several practical applications involving visibility analysis are illustrated for geographical problem-solving. Finally, existing software and toolboxes for visibility analysis are introduced.


AM-06 - Grid Operations and Map Algebra
Grid operations are manipulation and analytical computations performed on raster data. Map Algebra is a language for organizing and implementing grid operations in Geographic Information Systems (GIS) software, and is typically categorized into Local, Focal, and Zonal functions, where each function typically ingests one or more grids and outputs a new grid. The value of a specific grid cell in the output grid for Local functions is determined from the value(s) of the analogous cell position(s) in the input grid(s), for Focal functions from the grid cell values drawn from a neighborhood around the specific output grid cell, and for Zonal functions from a set of grid cells specified in a separate zone grid. Individual functions within a category vary by applying a different arithmetic, statistical, or other type of operator to the function. Map Algebra also includes Global and Block function categories. Grid operations can be categorized as data manipulation procedures or within domain-specific applications, such as terrain analysis or image processing. Grid operations are employed in a variety of GIS-based analyses, but are particularly widely used for suitability modeling and environmental analyses.