Analytics and Modeling

This knowledge area embodies a variety of data driven analytics, geocomputational methods, simulation and model driven approaches designed to study complex spatial-temporal problems, develop insights into characteristics of geospatial data sets, create and test geospatial process models, and construct knowledge of the behavior of geographically-explicit and dynamic processes and their patterns.

Topics in this Knowledge Area are listed thematically below. Existing topics are in regular font and linked directly to their original entries (published in 2006; these contain only Learning Objectives). Entries that have been updated and expanded are in bold. Forthcoming, future topics are italicized. 

 

Methodological Context Surface & Field Analyses Space-Time Analysis & Modeling
Geospatial Analysis & Model Building Modeling Surfaces Time Geography
Changing Context of GIScience Gridding, Interpolation, and Contouring Capturing Spatio-Temporal Dynamics in Computational Modeling 
Building Blocks Inverse Distance Weighting GIS-Based Computational Modeling
Overlay & Combination Operations Radial Basis & Spline Functions Computational Movement Analysis
Areal Interpolation Polynomial Functions Volumes and Space-Time Volumes
Aggregation of Spatial Entities Kriging Interpolation  
Classification & Clustering LiDAR Point Cloud Analysis Geocomputational Methods & Models
Boundaries & Zone Membership Intervisibility, Line-of-Sight, and Viewsheds Cellular Automata
Spatial Queries Digital Elevation Models & Terrain Metrics Agent-based Modeling
Buffers TIN-based Models and Terrain Metrics Simulation Modeling
Grid Operations & Map Algebra Watersheds & Drainage Networks Artificial Neural Networks
Data Exploration & Spatial Statistics 3D Parametric Surfaces Genetic Algorithms & Evolutionary Computing 
Spatial Statistics Network & Location Analysis Big Data & Geospatial Analysis
Spatial Sampling for Spatial Analysis Intro to Network & Location Analysis Problems of Large Spatial Databases
Exploratory Spatial Data Analysis (ESDA) Location & Service Area Problems Pattern Recognition & Matching
Point Pattern Analysis Network Route & Tour Problems Artificial Intelligence Approaches
Kernels & Density Estimation Modelling Accessibility Intro to Spatial Data Mining
Spatial Interaction Location-allocation Modeling Rule Learning for Spatial Data Mining
Cartographic Modeling The Classic Transportation Problem Machine Learning Approaches
Multi-criteria Evaluation   CyberGIS and Cyberinfrastructure
Grid-based Statistics and Metrics   Analysis of Errors & Uncertainty
Landscape Metrics   Error-based Uncertainty
Hot-spot and Cluster Analysis   Conceptual Models of Error & Uncertainty
Global Measures of Spatial Association   Spatial Data Uncertainty
Local Indicators of Spatial Autocorrelation   Problems of Scale & Zoning
Simple Regression & Trend Surface Analysis   Thematic Accuracy & Assessment
Geographically Weighted Regression   Stochastic Simulation & Monte Carlo Methods
Spatial Autoregressive Models   Mathematical Models of Uncertainty
Spatial Filtering Models   Fuzzy Aggregation Operators

 

AM-82 - Microsimulation and calibration of agent activities
  • Describe a “bottom-up” simulation from an activity-perspective with changes in the locations and/or activities the individual person (and/or vehicle) in space and time, in the activity patterns and space-time trajectories created by these activity patterns, and in the consequent emergent phenomena, such as traffic jams and land-use patterns
  • Describe how various parameters in an agent-based model can be modified to evaluate the range of behaviors possible with a model specification
  • Describe how measurements on the output of a model can be used to describe model behavior
AM-44 - Modelling Accessibility

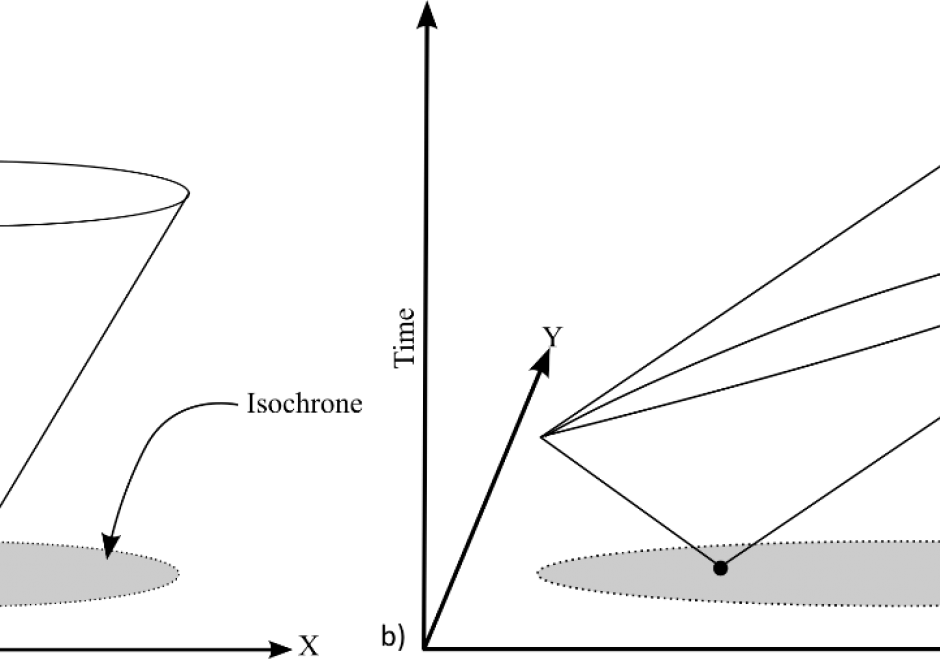
Modelling accessibility involves combining ideas about destinations, distance, time, and impedances to measure the relative difficulty an individual or aggregate region faces when attempting to reach a facility, service, or resource. In its simplest form, modelling accessibility is about quantifying movement opportunity. Crucial to modelling accessibility is the calculation of the distance, time, or cost distance between two (or more) locations, which is an operation that geographic information systems (GIS) have been designed to accomplish. Measures and models of accessibility thus draw heavily on the algorithms embedded in a GIS and represent one of the key applied areas of GIS&T.

AM-13 - Multi-criteria evaluation
  • Describe the implementation of an ordered weighting scheme in a multiple-criteria aggregation
  • Compare and contrast the terms multi-criteria evaluation, weighted linear combination, and site suitability analysis
  • Differentiate between contributing factors and constraints in a multi-criteria application
  • Explain the legacy of multi-criteria evaluation in relation to cartographic modeling
  • Determine which method to use to combine criteria (e.g., linear, multiplication)
  • Create initial weights using the analytical hierarchy process (AHP)
  • Calibrate a linear combination model by adjusting weights using a test data set
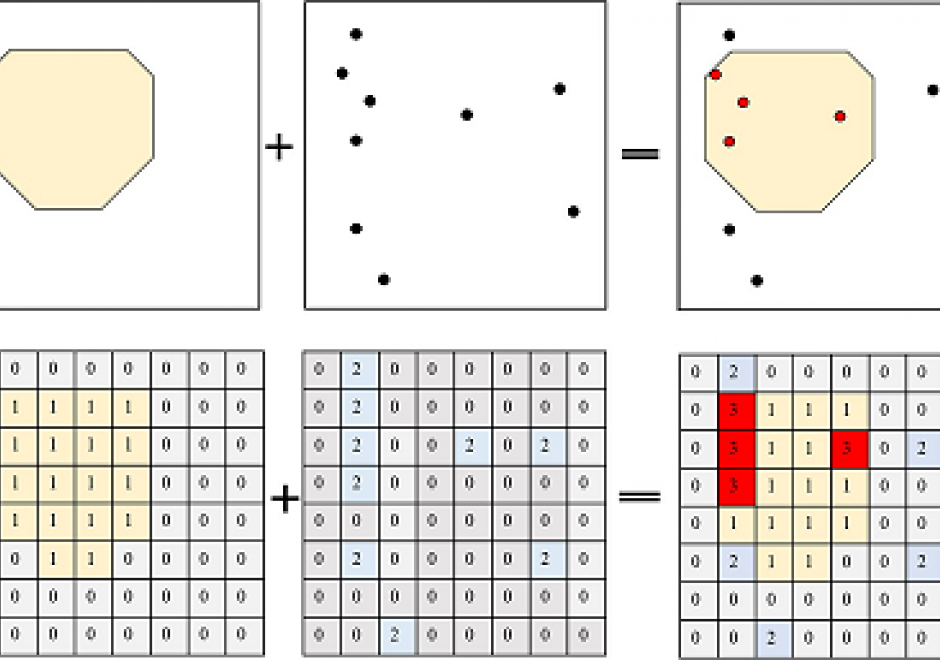
AM-04 - Overlay

Overlay operation is a critical and powerful tool in GIS that superimposes spatial and attribute information from various thematic map layers to produce new information. Overlay operations facilitate spatial analysis and modeling processes when being used with other spatial operations (e.g. buffer, dissolve, merge) to solve real-world problems. For both vector and raster data models, the input layers need to be spatially aligned precisely with each other to ensure a correct overlay operation. In general, vector overlay is geometrically and computationally complex. Some most used vector overlay operations include intersection, union, erase, and clip. Raster overlay combines multiple raster layers cell by cell through Boolean, arithmetic, or comparison operators. This article provides an overview of the fundamentals of overlay operations, how they are implemented in vector and raster data, and how suitability analysis is conducted.

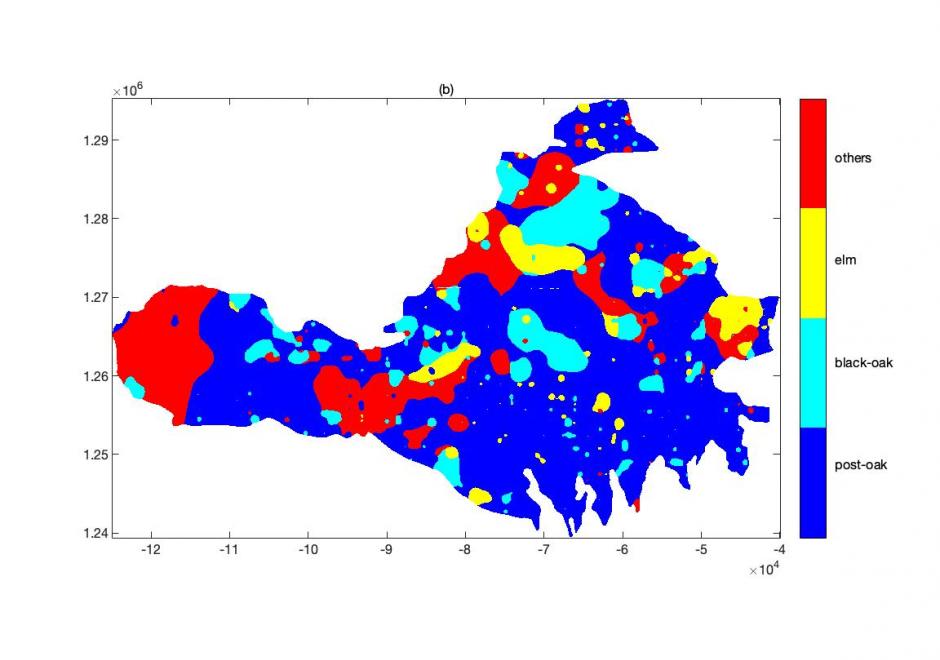
AM-38 - Pattern Recognition and Matching

People recognize and characterize patterns to understand the world. Spatial data exhibit distinctive characteristics that render most aspatial recognition and matching methods unsuitable or inefficient. In past decades, a plethora of methods have been developed for spatial pattern recognition and matching to account for these spatial characteristics. This entry first focuses on the methods of spatial pattern recognition, including an overview of the basic concepts and common  types. Methods for spatial pattern matching are then introduced. An example scenario of the distribution of tree species in the Arbuckle Mountains of south-central Oklahoma illustrates covered concepts. The entry concludes with brief remarks on continuing challenges and future directions in spatial pattern recognition and matching in the Big Data and artificial intelligence era.

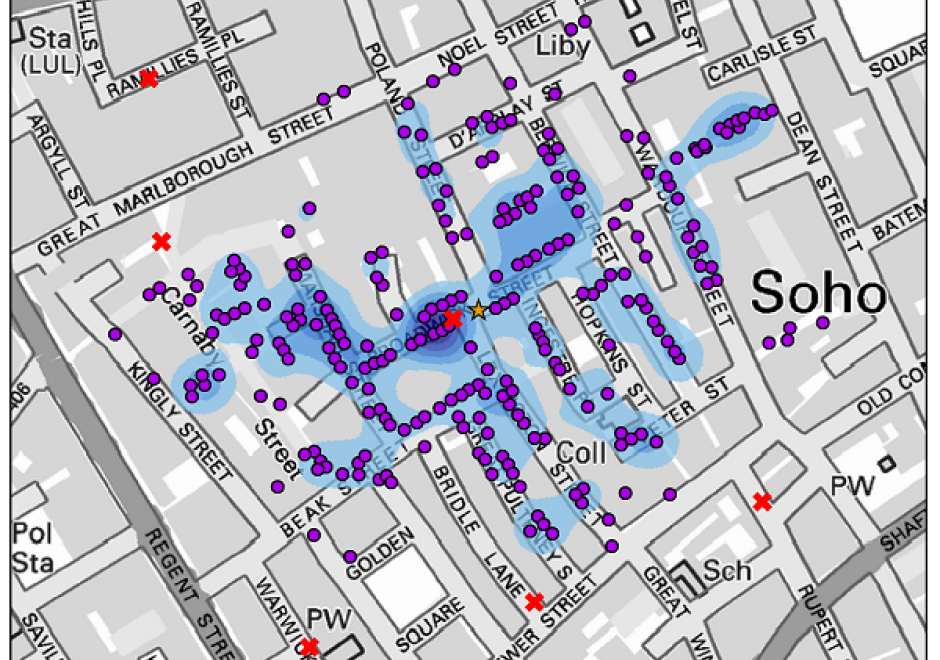
AM-07 - Point Pattern Analysis

Point pattern analysis (PPA) focuses on the analysis, modeling, visualization, and interpretation of point data. With the increasing availability of big geo-data, such as mobile phone records and social media check-ins, more and more individual-level point data are generated daily. PPA provides an effective approach to analyzing the distribution of such data. This entry provides an overview of commonly used methods in PPA, as well as demonstrates the utility of these methods for scientific investigation based on a classic case study: the 1854 cholera outbreaks in London.

AM-27 - Principles of semi-variogram construction
  • Identify and define the parameters of a semi-variogram (range, sill, nugget)
  • Demonstrate how semi-variograms react to spatial nonstationarity
  • Construct a semi-variogram and illustrate with a semi-variogram cloud
  • Describe the relationships between semi-variograms and correlograms, and Moran’s indices of spatial association
AM-87 - Problems of currency, source, and scale
  • Describe the problem of conflation associated with aggregation of data collected at different times, from different sources, and to different scales and accuracy requirements
  • Explain how geostatistical techniques might be used to address such problems
AM-68 - Rule Learning for Spatial Data Mining

Recent research has identified rule learning as a promising technique for geographic pattern mining and knowledge discovery to make sense of the big spatial data avalanche (Koperski & Han, 1995; Shekhar et al., 2003). Rules conveying associative implications regarding locations, as well as semantic and spatial characteristics of analyzed spatial features, are especially of interest. This overview considers fundamentals and recent advancements in two approaches applied on spatial data: spatial association rule learning and co-location rule learning.

AM-28 - Semi-variogram modeling
  • List the possible sources of error in a selected and fitted model of an experimental semi-variogram
  • Describe the conditions under which each of the commonly used semi-variograms models would be most appropriate
  • Explain the necessity of defining a semi-variogram model for geographic data
  • Apply the method of weighted least squares and maximum likelihood to fit semi-variogram models to datasets
  • Describe some commonly used semi-variogram models

Pages