AM-97 - An Introduction to Spatial Data Mining

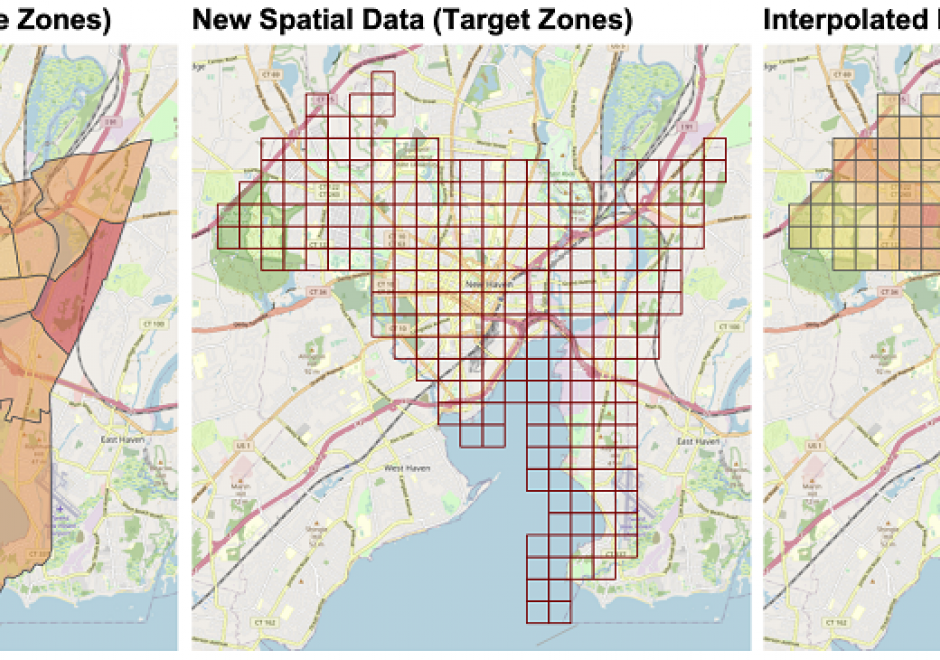
The goal of spatial data mining is to discover potentially useful, interesting, and non-trivial patterns from spatial data-sets (e.g., GPS trajectory of smartphones). Spatial data mining is societally important having applications in public health, public safety, climate science, etc. For example, in epidemiology, spatial data mining helps to nd areas with a high concentration of disease incidents to manage disease outbreaks. Computational methods are needed to discover spatial patterns since the volume and velocity of spatial data exceed the ability of human experts to analyze it. Spatial data has unique characteristics like spatial autocorrelation and spatial heterogeneity which violate the i.i.d (Independent and Identically Distributed) assumption of traditional statistic and data mining methods. Therefore, using traditional methods may miss patterns or may yield spurious patterns, which are costly in societal applications. Further, there are additional challenges such as MAUP (Modiable Areal Unit Problem) as illustrated by a recent court case debating gerrymandering in elections. In this article, we discuss tools and computational methods of spatial data mining, focusing on the primary spatial pattern families: hotspot detection, collocation detection, spatial prediction, and spatial outlier detection. Hotspot detection methods use domain information to accurately model more active and high-density areas. Collocation detection methods find objects whose instances are in proximity to each other in a location. Spatial prediction approaches explicitly model the neighborhood relationship of locations to predict target variables from input features. Finally, spatial outlier detection methods find data that differ from their neighbors. Lastly, we describe future research and trends in spatial data mining.




AM-79 - Agent-based Modeling
Agent-based models are dynamic simulation models that provide insight into complex geographic systems. Individuals are represented as agents that are encoded with goal-seeking objectives and decision-making behaviors to facilitate their movement through or changes to their surrounding environment. The collection of localized interactions amongst agents and their environment over time leads to emergent system-level spatial patterns. In this sense, agent-based models belong to a class of bottom-up simulation models that focus on how processes unfold over time in ways that produce interesting, and at times surprising, patterns that we observe in the real world.