DA-09 - GIS&T and Geodesign
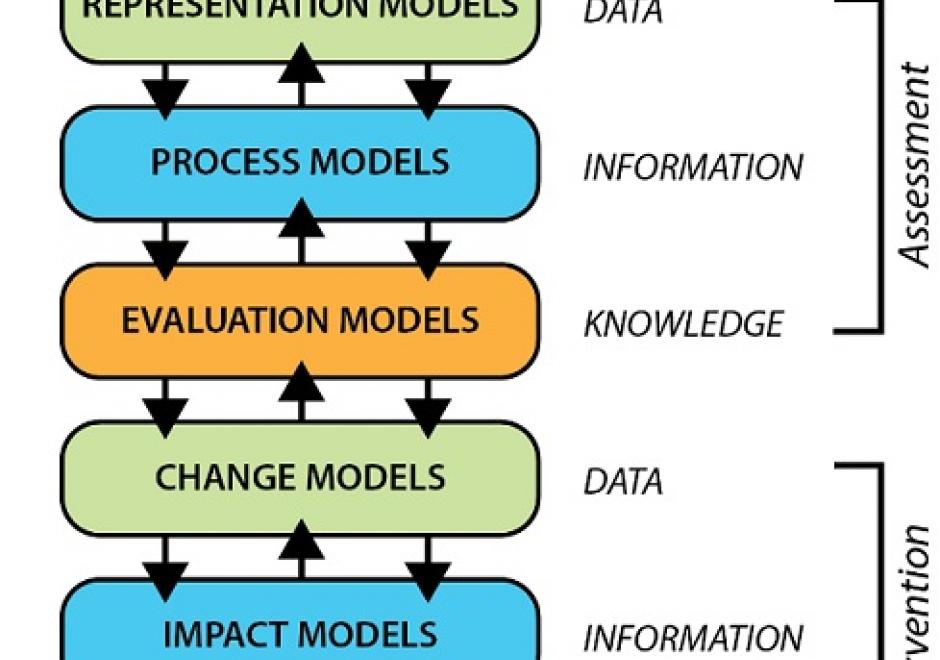
Geodesign leverages GIS&T to allow collaborations that result in geographically specific, adaptive and resilient solutions to complex problems across scales of the built and natural environment. Geodesign is rooted in decades of research and practice. Building on that history, is a contemporary approach that embraces the latest in GIS&T, visualization, and social science, all of which is organized around a unique framework process involving six models. More than just technology or GIS, Geodesign is a way of thinking when faced with complicated spatial issues that need systematic, creative, and integrative solutions. Geodesign holds great promise for addressing the complexity of interrelated issues associated with growth and landscape change. Geodesign empowers through design combined with data and analytics to shape our environments and create desired futures.

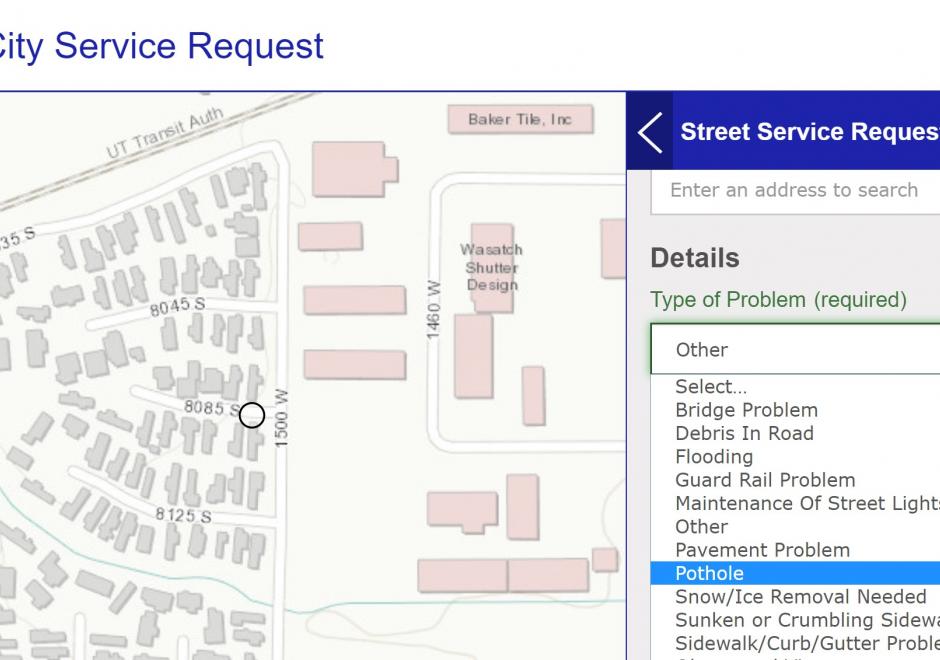




DA-16 - GIS&T and Forestry
GIS applications in forestry are as diverse as the subject itself. Many foresters match a common stereotype as loggers and firefighters, but many protect wildlife, manage urban forests, enhance water quality, provide for recreation, and plan for a sustainable future. A broad range of management goals drives a broad range of spatial methods, from adjacency functions to zonal analysis, from basic field measurements to complex multi-scale modeling. As such, it is impossible to describe the breadth of GIS&T in forestry. This review will cover core ways that geospatial knowledge improves forest management and science, and will focus on supporting core competencies.